Introduction:

• An Individual is a thing (person, animal, place, etc.) being studied in a data set. Columns in a data table

• A Variable is an characteristic that holds information for different induvial. Rows in a data table

• A Categorical Variable assigns labels that place each individual into a particular group, called a category

• A Quantitative Variable takes number values that are quantities—counts or measurements.

  • GPA & Children in Family are examples of this

  • Grade Level, Homework Last Night, and other ranges are not quotative.

  • 2 Types of Quotative Variables: Discrete & Continuous variables.

    • A Discrete Variable comes from counting something (like number of languages spoken).

    • A Continuous Variable comes from measuring something (like ones height).

• A Distribution tells us how a variable is spread out and positioned.

  • Usually a distribution is in the form of a graph: … shows the distribution of left vs right handed people in a bar graph.

  • Usually a pattern in the data

1.1 Analyzing Categorical (Words) Data:

• A Frequency Table shows how many times a value (individual) appears

  • Ex: 3 people got a 75% on a test

• A Relative Frequency Table shows the pieces / percent(s) of each value (individual).

• A Bar Graph shows each categorical variable as a bar. The bar’s heights shows the frequency.

  1. Draw & label the axes: Categorical variables under horizontal axis, frequency on vertical axis.

  2. “Scale” the axes: Write the names of the Categorical Variables & start at 0 for frequency.

  3. Draw bars above category names: Correspond w/ frequency & leave gaps between bars

• A Pie Chart shows each categorical variable as a slice of the “pie”, adding to 100%.

• A Two-Way Table shows the relationship between two categorical variables (Columns like: No, Yes, Total)

• A Joint Relative Frequency is the percent/proportion between 2 categorical variables.

  • Ex: Proportion of people in a club & use a car is 445/1526 = 0.292 = 29.2%

• To compare the distribution (data) of categorical variables, use these graphs:

  • Side-By-Side Bar Graphs, Segmented Bar Graph, & Mosaic Plot.

  • They all pretty much do the same thing. See the image below.

    

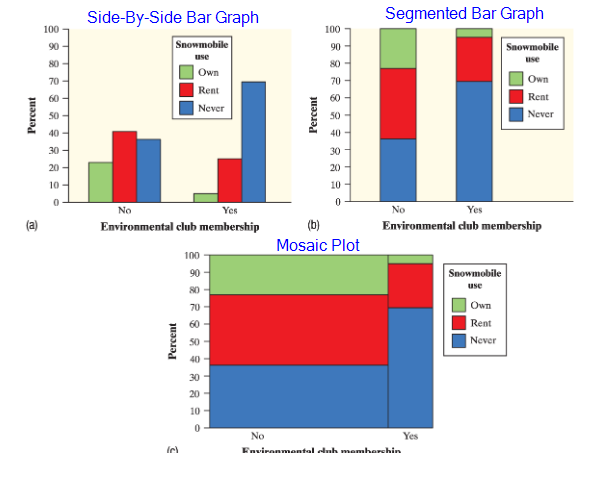
• An Association can help predict the outcome of one variable based on another variable.

1.2 Quantitive (Numerical) Data with Graphs

• A Dotplot uses dots above a number line to show where each value is.

  

Graph Shape:

• When looking at a graph (like a dotplot), look at it’s shape.

  • Ensure to look at it from a distance, ignore minor ups and downs

• Describe if the graph is symmetric or is clearly skewed

  • Symmetric when the right side is a mirrorish of the left side.

  • Skewed to Right when “bump” is to left & “tail” faces right

  • Skewed to Left when “bump” is to right & “tail” faces left

• The direction of skewedness is towards the long tail, not where there is large clusters.

Quantitive Distributions:

• Remember: A distribution is how a variable is spread out and positioned.

• To Find a Distribution look for an overall pattern by its shape, outliers, center, and variability.

  • Shape: Symmetric, Skewed Left, or Skewed Right

  • Outliers: Should Be Ignored when describing

  • Center: Mean or Median

    • If shape is Skewed or has Outliers, use Median

    • if shape is Symmetric, use mean

  • Variability: Range, IQR (Q3 - Q1), or Standard Deviation

Other Graphs:

• Stemplots (Aka Stem & Leaf Plots) shows data separated in two parts: stem & leaf (1st Image)

  • Stem is everything but the 1st digit, leaf is the final digit.

  • Make sure to have a key! Ex: 8|2 = 82 beats per minuet

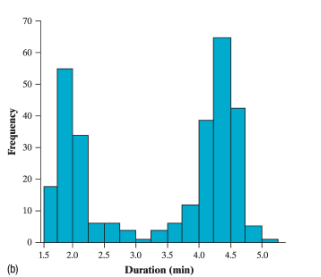
• Histograms show each inverval values as a bar graph (2nd Image)

  • This is useful since there’s usually a lot of data points, and histograms reduce the number of bars that will be present on the graph.

  • Basically a bar graph but with a range.

1.3 Describing Quantitive Data with Numbers

• Best way to measure center is using its mean

• The Mean is the average of the individual data values

  • To find the mean, add all the values and divide by the total number of data values

• A Statistic is a number that describes a characteristic of a sample

• A Parameter is a number that describes some characteristic of a population

• A statistic measurement is Resistant when not sensitive to outliers.

• The Median is the midpoint of a distribution

  • Mean < Median when Shape is Skewed Left

  • Mean > Median when Shape is Skewed Right

  • Mean = Median when Shape is Symmetric

• The Range is the distance between the minimum and maximum value in the data

  • Range is useful since sometimes the shape and center can be the same.

• Standard Deviation measures variance (Q1 & Q3) from the mean (Q2)

  1. Find the mean

  2. Calculate the deviation of each value: deviation = value - mean

  3. Square and add all the deviations

  4. Divide the answer by n - 1 (Where n is the number of values)

  5. Take the square root of the answer

  • The Variance is the Standard Deviation squared

• The Interquartile Range (IQR) measures the distance between the 3rd quartile and 1st quartile.

  • Formula: IQR = Q3 - Q1

  • Q1 is the median for the first half of the data min → Q2 (Median)

  • Q2 is the median of the entire data set min → max

  • Q3 is the median for the last half of the data Q2 → max

• The 1.5 * IQR Rule provides a mathematical way to find outliers

  • Low Outliers < Q1 - 1.5 * IQR

  • High Outliers > Q3 + 1.5 * IQR

  • If the result of the inequality is true, an outlier exists.