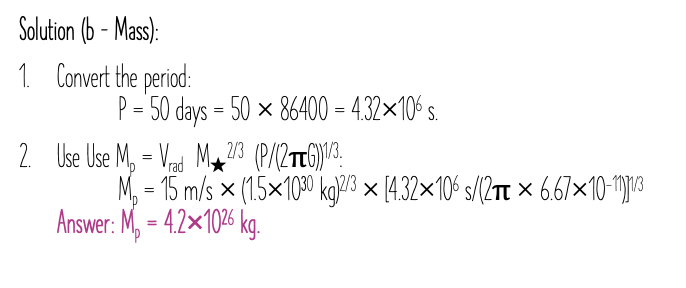Chapter 7 - The Planetary

Quiz 6

Our Solar System

• planets are large, spherical isolated bodies that orbit a star

  • must clear debris from its own path

• a planetary system is a system of a star, planets, moons, and smaller bodies

Nebular Hypothesis

• a rotating cloud of interstellar gas gradually collapses and flattens to form a disk

• the sun forms at the center and planets form from the disk

• modern theory calculates conditions required for a cloud to collapse under the force of gravity

  • self-gravity is the attraction between parts of an object tha tpull outer layers toward the center

  • self-gravity is opposed by structural strength, gas pressure, or radiation pressure

  • in a stable object, inward and outward forces are balanced

• Evidence

  • Astronomical Images

    • young stars are seen to be surrounded by rotating disks of gas and dusts

  • Motion of Planets

    • evidence of our own planets support the nebular hypothesis

      • all planets orbits the sun in the same direction and in the same flat plane

      • we can deduce that the planets must have formed from the same flat, rotating disk of material

  • Meteorites

    • contain hints to the solar system’s formation as well

    • many are mixtures of smaller rocks or pebbles, suggesting formation through a process of aggregation

Thought Experiment: Temperature of a Balloon

• make the circumference at the widest part of the balloon

• cold - shrink

• warm - expand

• when temp drops, outward pressure decreases, balloon shrink sunder self-gravity

• illustration of a system maintaining hydrostatic equilibrium

  • ensures stars and planets are stable systems

7.2 The Solar System Began with a Disk

Solar System Beginnings

• a collapsing cloud of interstellar gas formed a protostar and protoplanetary disk

• protostar - a large ball of gas; not hot enough to be a star

  • protoplanetary disk: flat, orbiting disk of gas and dust

Growth of Particles

• within the disc, small articles will collide and stick

• small particles are blown into larger ones by gas motions

• this leads to larger particles (~1km in size) called planetesimals

• at a size of 1km, gravity takes over and pulls nearby objects into the planetesimal

• through growth driven by gravity, planetesimals combine to form planets

• today’s remaining planetesimals are asteroids and comets

  • asteroids - rock and metal

  • comets - ice and rock

What an astronomer sees

• notice the brown clumps that are too dense to see through these are sites of star formations

• notice the jets of materials being ejected by newly formed stars

Visual Summary: The Collapsing Cloud

1. as gravity causes the collapse of a slowly rotating clump, it rotates faster

2. rotation slows collapse perpendicular to but not parallel to the axis, so the clump flatters

3. eventually the clump collapses from the inside out, and an accretion disk and protostar form

Formation of a Flat Disk

• most of the as lands on a accretion disk, which continues the rotation

• the angular momentum of the interstellar cloud is conserved and ends up in the accretion disk

• material in the accretion disk either becomes part of the protostar, forms planets, or is ejected back into interstellar space

Definition of Angular Momentum

• angular momentum is associated with rotating objects. It depends on

  • rotational velocity

  • mass

  • mass distribution

Conservation of Angular Momentum

• conserved quantity. It cannot change unless an external force is applied

• the figure skater’s angular momentum does not change, but as she pulls in her arms, she rotates faster

• p=mv

• L=Iw

• I=mr²

• L=mr²v/r

• L=mvr {Angular Momentum (Point Mass)}

Angular Momentum on a Sphere

I = 2/5mr²

L = Iw = 2/5mr²w

L = 2/5 mr²v/r

L=2/5mrv (v=2pir/p)

L=4/5(pimr/P)

Angular momentum deends on an object;s mass, size, and speed. If a giant giant gas intitially rotaes slowly, what will happen to tilts

• speed up

calculate orbital angular momentum, we need to know Jupitaer’s mass, velocity and size of orbit

• 1.94 × 10^43 m²/s

for a uniform sphere, spin angular momentum is give by 4pimR²/5P

• for the sun

  • 1.14 × 10^42 m/s

7.3 The inner disk and outer disk formed at temperatures

Conversion of Energy

• gas the fas cloud shrinks, its gravitational potential energy is converted to kinetic energy, radiative energy, and thermal energy. Energy is conserved

• thermal energy is greater in the inner portion of the disk

• gravitational energy is converted to heat more in inner disk than outer disk

• the inner disk is closer to protostar, which heat sup the surrounding material

Disk Composition

• the composition of dust grains depends on temperature

• inner disk - only refractory materials can form or remain

• outer disk - can also have volatile materials such as ices and organic material

• Refractory - does no melt at high temperature

• Volatile - can melt or evaporate at moderate temperatures

• Organic - contains carbon-hydrogen bonds

Atmospheres

• the primary atmosphere is the gas initially gathered from the disk

  • primarily hydrogen and helium (low-mass gases)

  • the process of gathering atmosphere is called core accretion-gas capture

• Secondary atmospheres occur around some low-mass planets because he initial atmosphere is lost

  • the low-mass planets do not have enough gravity to keep the initial atmosphere form escaping

  • volcanoes emit heavy gases from the planetary interiors that the planet can hold on to for a very long time

  • comets bring water and other volatiles to planets, which evaporate and add to the secondary atmosphere

Quiz 7

Gas Giants

• the giant planets are jupiter, saturn, uranus, and neptune

• farther from the sun, planetesimals could contain volatile and organic materials

  • can also form ices

• planetesimals grew large enough that their gravity could capture nearby gas

  • primarily formed of hydrogen and helium

• the model of giant planet formation is called the core accretion-gas capture

• mini accretion disks formed aorund these larg epanetesimals (planet cores( and began funneling material onto them

• large moons formed from the mini accretion disks

• gravitational energy was converted into thermal energy, heating these planets

• the forming sun emits winds and jets thta the planetary nebuyla of most gas

• jupiter only had 10 million years to form before the most gas was lost

The formation of our solar system: other objects

• moon - a natural satellite of a planet of asteroid

  • they are sometimes formed in accretion disks around planets

• dwarf planets: round objects that orbit the usn but have not cleared their orbits of smaller bodies

• asteroids - small bodies found inside Jupiter’s orbit

• comet nuclei - icy planetesimals in outer Solar system that survived planetary accretion

cataclysmic impacts

• in the early solar system, impacts from remaining planetesimals were common

• impacts resulted in heavily cratered surfaces (such as on the moon and mercury)

• a giant impact formed our moon

• impacts knocked uranus on its side, so it rotates perpendicular to its orbit planeand Venus rotates backwards

7.5 Planetary systems are common

Planetary systems are common

• disks are commonly seen around young stars

• this suggests that plaents regularly form around other stars

• an exoplanet is a body with a mass less than 13 Jupiter masses that orbits a star other than the sun

Exoplanets

• March 2025, 5,856 known exoplanets have been confirmed

• there are several techniques used to find these planets:

  • radial velocity method

  • transit method

  • microlensing method

  • direct imaging

  • astrometry

Transit Method

• a planet passing in front of a star (transiting) decreases the total brightness of the star

• because of the space missions Kepler and TESS, this is the most common way to find planets

• the transit method can be used to calculate the size of a planet

• planets can be distinguished by:

  • different periods

  • different depths

  • different durations

Estimating the Radius of an exoplanet

• with the transit method, astronomers can determine a planet’s radius:

  • fractional reduction in light = Area of Planet/area of star = piR²planet/piR²star = R²planet/R²star

• the radius if a star is estimated from the star’s temperature and luminosity

Kepler-11

• Kepler-11 is a system of at least six planets. The host star has a radius 𝑅star = 7.7 × 10^5 . Planet Kepler-11c causes a 0.077 percent reduction in light. Now we can solve for Kepler-11c’s radius:

• 0.00077 = R² Kepler-11c/(7.7 X 10^5km)²

• R²Kepler-11c = 4.6 × 10^8km²

• RKepler - 11c = 2.1×10^4 km = 3.3Rearth

Radial Velocity Method

• gravity

• motion of star can be detected by doppler shifts

• some stars have periodic velocity changes: therefore, they are orbited by planets

• the radial velocity method only works for giant planets around nearby stars

• the method can be used to determine a planet’s orbit

Radial Velocity Method Illustration

• light from a star is blueshifted as it moves toward us, causing a negative velocity shift

• light from the star is redshifted as it moves away from us, causing a positive velocity shift

• most negative radial velocity = star moving primarily towards observer (can als be moving up or down)

• most positive radial velocity - star moving primarily away from observer

• the planet is orbiting the center of mass

• Planet’s motion if opposite to that star

Estimating the size of a planet’s orbit

• the radial velocity method can be used to determine the size of a planet’s orbit

• to see how, recall Newton’s verion of Kepler’s third law

• P² = 4pi²/G A³ /M → A³ = G/4pi² M * P²

  • p = period of orbit

  • m = mass of star and planet

  • a = semi-major axis

  • g = 6.67 × 10^ -20 km³/kg s²

For planet HD70642b

• P = 5.7 yr = 1.8 × 10^8 s

• M = 2 × 10^ 30 kg

• Now, we solve

  • A³ = G/4pi² X M X P²

  • 6.67×10^ -20 km³/kg s² / 4pi² x (2×10^ 30 kg) x (1.8 × 10^8 s)²

  • A³ = 1.1 × 106^ 26 km³

  • A = 4.8 × 10^8 km = 3.2 AU

Newton’s form of Kepler’s 3rd Law

• P² = 4pi²/GM(star)(A³)

• Vp(velocity of planet) =2piA(planet)/P(planet)

Question

• a star has a radius of 7.0 × 10^5 km. A transit observation shows that the star’s brightness drops by 1.0% (i.e LambdaF = 0.0100). Calculate the planet’s radius.

• LambdaF = Rp²/Rstar²

  • lambdaf R(star)² = Rp²

  • square root(Flux)Rstar = Rp

  • sqaure root (0.01)(7.0 × 10^5) = 70,000 km

• a star has a radius of 1.5 × 10^6 km. Durng transit, the brightness decreases by 0.25% (i.e LambdaF = 0.0025). Calculate the planet’s radius.

  • 75,000km

• a star with a mass of 2.0 × 10^ 30 is observed to have a maximum radial velocity shift of 10 m/s due to an orbiting planet. The orbital period if 100 days.

• What is the estimated planet mass?

• Using the period and star’s mass, what is the semi-major axis of the planet’s orbit?

  • estimated planet mass

    • Convert period to seconds

    • use Mp = Vstar * mstar^ 2/3 (Pp/2piG)^ 1/3

  • semimajor axis

    • use Kepler’s third law in the form

      • a=[GMstar P²/(4pi²)]^ 1/3

      • substitite the known values

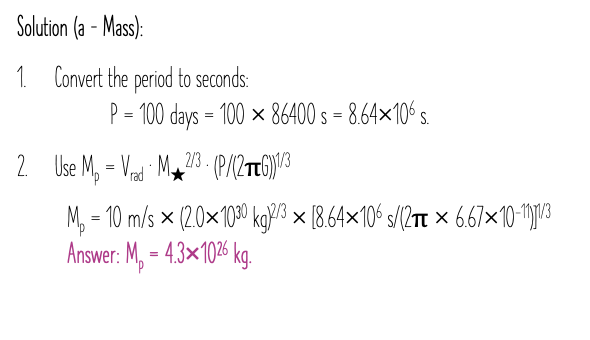
• a star with a mass of 1.5 × 10^ 30 and a radius of 8.0 × 10^5 km. Observations reveal a transit dip of 0.50% (lambdaF = 0.0050) and the stars maximum radial velocity is 15m/s. The orbital period is 50 days.

  • What is the planet’s radius?

  • What is the estimated planet mass?

  • What is the semi-major axis of the planet’s orbit?

    • Radius

      • 

    • Planet’s Mass

      • 

    • Semi-major axis

      • 

Other Methods

• direct imaging - taking a picture of the planet directly

  • diffcult because the stars are much brighter than the planets

  • other methods are needed to follow up

• microlensing - makes a star temporarily brighter through a planet’s gravity focusing its light

• Astrometry - detects planets by precisely measuring the change in position of a star in the plane of the sky

Types of Exoplanets: Hot Jupiters

• hot jupiters are jupiter-sized planets that orbit solar-type stars in very close orbits

• they are very easy to detect

  • they cause a big wobble on their star

  • they trnsit regularly and casue and easily noticebale drop in brightness

• they surpirsed astronomers becayse, according to the nebular theory, such volatile-rich planets should not be so close to the star

• planetary migration occus when a planet changes irs orbit after formation