PY 131 Chapter 14: Gases

Gases

Gases are also fluids and share the same physics as liquids. They have:

• a density
• pressure,
• can exert buoyancy forces

As the density of the gas decreases, the potential energy between the atoms/molecules which make up the gas also decreases.

An ideal gas has zero potential energy.

• Air is close to an ideal gas.

Atmospheric Pressure

• The atmosphere exerts pressure on all objects exposed to it.
• The exact value depends upon the weather but on average the pressure at sea level is 1.01325 x 105 N/m2 = 101.325 kPa.
  • This average pressure of the atmosphere is used as a unit of pressure
    called the 'atmosphere'.
  • Atmospheric pressure is equivalent to the weight of a column of water 10.3 meters high.
• Another common unit of pressure is the bar defined to be 1 bar = 1.000 x 105 N/m2 .
• ==Gauge Pressure== is the pressure of gasses measured by pressure gauges (such as at the gas station).
• Pressure gauges measure pressures relative to the atmosphere.
• To get the absolute pressure of the gas you need to add the pressure of the atmosphere.
  • a gas with an absolute pressure of 2 atmospheres would measure 1-atmosphere gauge pressure.

Measuring Pressure

• There are many devices for measuring pressure.

• They all typically use the equation

  • P2 - P1 = −ρ g h

• to relate pressure differences to the height of a column of liquid h of a given density ρ.

• The simplest is the manometer.

• If P1 > P2 then h > 0

• If P1 < P2 then h < 0

  

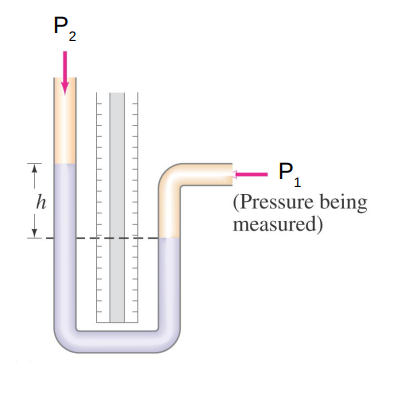
• Any liquid may be used inside the manometer as long as its density is known.

• The most common choice is mercury Hg.

• Measuring h and specifying the liquid, allows you to determine the gas pressure being measured.

• This leads to another unit of pressure called the torr or mm-Hg.

• 1 torr = 1 mm-Hg = 133 Pa, 1 atm = 760 torr.

• A similar device to a manometer is the barometer.

• A tube is filled with a liquid and then inverted with the open end of the tube beneath the surface of a bath of the liquid.

• Upon inversion, the fluid in the tube will drop creating a vacuum at the top of the tube.

• The height of the column of liquid left in the tube will change with the pressure of the gas upon the bath.

  

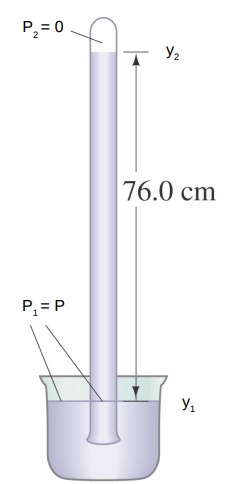
• Using

  • P2 - P1 = − ρ g h
  • P2 = 0 so set P1 = P
  • h= P/ρg

• For mercury, a column of height 76 cm can be supported if the gas pressure is 1 atmosphere.

  • For water, the height is 10.3 m.

• Again, a change in pressure changes the height of the liquid column.

• The liquid is not ‘sucked up’ - there is no such thing as a suction force.

• The liquid is pushed up by the pressure of the atmosphere.

  

• Since atmospheric pressure decreases with altitude, barometers can be used at altimeters.

EXAMPLE 1

In a mercury barometer at atmospheric pressure, the height of the column of mercury in a glass tube is 760 mm. If another mercury barometer is used that has a tube of larger diameter, how high will the column of mercury be in this case?

• The height of the column of mercury in a barometer is determined by the atmospheric pressure on the surface of the mercury. The pressure does not depend on the diameter of the tube, so the height of the column will be the same regardless of the tube diameter. Therefore, ==the height of the column in the second barometer will also be 760 mm==.

Buoyancy In Gases

• A gas can also exert buoyancy forces upon an object exactly like a liquid.
• The buoyancy force from gas is
  • FB=ρF gV
• Where the volume of the object is V and the gas has a density of ρF.
• The weight of the displaced gas is typically small so the buoyancy force is often negligible.
  • Given the density of air, the buoyancy force upon an object with a volume of 1 cubic meter is ~12 N which is the weight of a 1.2 kg mass.
  • The buoyancy force from the air upon an average person is ~0.5 N.
• Balloons have buoyancy forces greater than their weight by having low densities / large volumes thus displacing large amounts of gas.
• An ideal balloon would have a vacuum inside but such a balloon would likely collapse due to the pressure from the gas.
• Air pressure is equivalent to a weight of ~1 kg on every square centimeter.
• By filling the balloon with another gas, the gas pressure on the inside of the balloon can cancel the pressure from the outside.
• The density of the gas used to fill the balloon has to be less than the density of the gas displaced.
  • Hydrogen and helium are both less dense than air.
• Air density decreases with height so as a balloon rises, the weight of the displaced air decreases.
• At some height, the buoyancy force matches the balloon’s weight and so there is now no net force.
• At this height, the balloon has neutral buoyancy.

EXAMPLE 1

A small iron ball and a large Styrofoam ball balance in air. If the air is evacuated, the larger ball

A. rises.

==B. falls.==

C. remains in place.

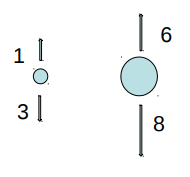
• The buoyancy force is greater than the weight (normal) force.

Fluids In Motion.

• A fluid can be considered to be composed of fluid elements – infinitesimally small fixed amounts (mass) of the fluid with variable volume.

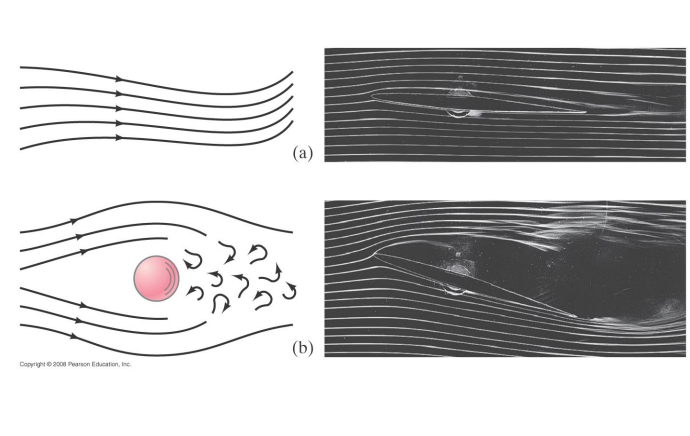
• The paths taken by fluid elements are called streamlines.

  • Streamlines can be visualized by using smoke or dyes

• Fluid flow can be divided into two main types: ==laminar flow and turbulent flow.==

• In laminar flow the streamlines do not cross.

• In turbulent flow the fluid streamlines do cross.

• Fluid kinetic energy is dissipated by viscosity (internal friction).

• In laminar flow the dissipation by viscosity is small, in turbulent flow it is large.

  

Continuity

• When a fluid flows through a pipe the fluid velocity changes with the size of the tube.

  • In narrow, constricted regions of the pipe the fluid velocity is high,
  • In wide regions the fluid velocity is low.

  

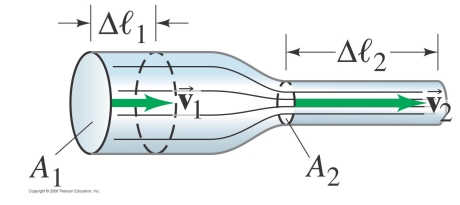
• The reason is that the mass of the fluid is conserved.

• In a given amount of time, the same mass of fluid must pass through every cross-sectional area of the pipe.

• At a given location the cross-sectional area of the pipe is A1, the fluid velocity is v1, and its density is ρ1.

• In time Δt the mass Δm of fluid which passes through A1 is

  • Δ m=ρ1 A1 v_1Δ t
  • Δ m / Δ t =ρ1 A1 v_1

• At a second location, the cross-sectional area of the pipe is A2, the fluid velocity is v2, and its density ρ_2.

• The same amount of fluid must pass through A_2 in time Δt

  • Δ m / Δ t =ρ2 A2 v_2

• In order to conserve mass, we require

• ρ1 A1 v1=ρ2 A2 v2

• This result is called the equation of continuity.

• If the fluid densities are the same at the two points (very common for liquids)

  • A1 v1=A2 v 2

• As the cross-sectional area of a pipe decreases, the speed of the fluid has to increase.

Fluid Energetics

• A fluid can have kinetic and potential energy and the fluid pressure – which is related to a force – can do work.

• The kinetic energy of a fluid with density ρ in volume V is

  • K=½m v 2=½ρV v 2

• The gravitational potential energy of the fluid is

• U_G=m g y=ρV g y

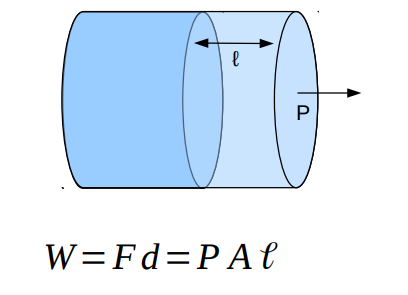
• If a fluid expands or contracts it does work

• The work done by a fluid with constant pressure P

  

Bernoulli's Principle

• Consider the fluid flow in a pipe with a variable cross-sectional area. A given fluid element in the pipe will have

  

• Assuming laminar flow, we can equate the mechanical energy of the fluid at one end of the pipe to the mechanical energy at the other, including any work done on or by the fluid.

• What we eventually find is

  • ½v1 2 +g y1+P1 /ρ1=½ v2 2 +g y2+P2 /ρ2

• This is known as Bernoulli's equation.

  

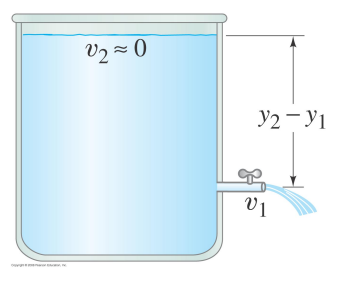
• Consider a tank of water with a spigot/tap/faucet.

• The fluid density is constant

• At both the top of the tank and at the spigot P = P0.

• If the tank is very big then v at the top of the tank is ~0.

  

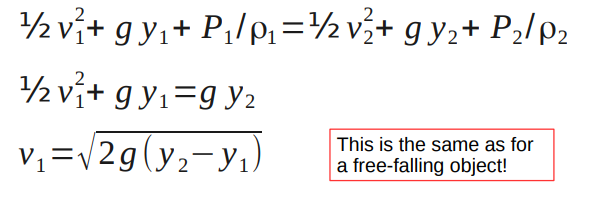
Venturi Effect

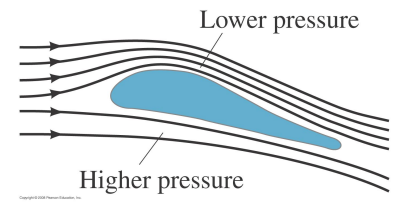
• According to Bernoulli's equation, as the kinetic and potential energies of a fluid increase, the pressure decreases.

  

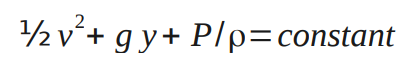
• Ergo a fast-moving fluid has a lower pressure than a slow-moving fluid (for a fixed y coordinate).

• This is called the ==Venturi effect.==

• The Venturi effect explains many different phenomena:

  • It contributes to how an airplane remains aloft,
  • Bernoulli grips (pick up an object without touching it)
  • Venturi tubes,

• Venturi meters are used to measure flow rates through pipes.

  

Dynamic Lift

• In order to remain aloft a plane must generate a 'lift' force to counter its weight.

• There are two contributions to the lift:

  • Above the wing, the streamlines are compressed therefore the air velocity increases. According to Bernoulli, the higher air velocity lowers the pressure there compared to the air below the wing. The pressure difference leads to an upward force on the wing.
  • The air is deflected downwards so the plane is deflected upwards by the conservation of momentum

  

EXAMPLE 1

• Explain why the roofs of houses lift off during hurricanes.
  • During a hurricane, strong winds create a region of low pressure on the roof. The high-speed winds passing over the roof create a Bernoulli effect, lowering the pressure above the roof. At the same time, there is high pressure below the roof due to the trapped air. The difference in pressure between the top and bottom of the roof can cause it to lift off, especially if there is damage or if it is not properly attached to the structure.

\