Lesson 2.2 | Reasoning

Inductive Reasoning

Conjecture

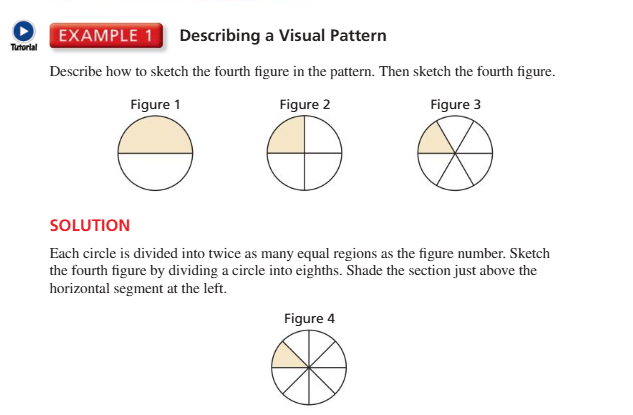
Inductive reasoning is when you gather clues or patterns and find that something is true based off of your evidence. This is called a conjecture. Think about it like seeing a pattern, and adding to it, or like an inferred guess.

Counterexample

A counterexample proves that a conjecture is false. Because for a conjecture to be true, it must be true for all cases, but if you can find one counterexample, you can say that it’s false

Deductive Reasoning

Deductive Reasoning uses facts, definitions, accepted properties, and the laws of logic to form an answer (logical argument). In contrast, inductive reasoning involves looking for patterns and making generalizations based on specific examples or observations. Additionally, deductive reasoning guarantees the truth of a conclusion if the premises are true, whereas inductive reasoning can lead to probable conclusions that may not always hold true.

Laws of Logic

Laws of Detachment

If the hypothesis of a true conditional statement is true, then the conclusion is also true.

Law of Syllogism

Think of it like the segment addition postulate, AB+BC = AC.

If AB, and BC cause AC, then hypotheses A causes conclusion C.