Chem Unit 8 - Acids and Bases (Kognity R3.1)

Intro to Brønsted-Lowry Acids and Bases: R3.1.1

Acids and bases are defined as either proton donors or acceptors with the Brønsted-Lowry theory. Protons are hydrogen atoms that have lost an electron, AKA hydrogen ions. In aqueous solutions, hydrogen ions exist as hydronium ions, or H3O+.

• Brønsted-Lowry acids donate a proton (hydrogen ion)

  • All Brønsted-Lowry acids contain hydrogen, as they must donate a proton.

• Brønsted-Lowry bases accept a proton (hydrogen ion)

  • All Brønsted-Lowry bases must have a lone pair of electrons to form a bond with the hydrogen ion donated by the acid.

The difference between a base and an alkali is an alkali is a base that is soluble in water, and produces hydroxide ions (OH-) when dissolved.

Substances that act as both an acid and a base are known as amphoteric, or amphiprotic. Water is one such example, as is hydrogen carbonate

Other examples of amphiprotic substances include:

• Hydrogen carbonate ions: HCO3 -

• Hydrogen sulfate ions: HSO4 -

• Dihydrogen phosphate: H2PO4 -

• Hydrogen phosphate: HPO4 2-

For example: when hydrogen chloride (HCl) gas dissolves in water, it donates a proton to the water molecule, H2O, which accepts the proton, making the HCl an acid, and the H2O a base.

Common acids:

• Hydrofluoric acid (HF)aq

• Hydrochloric acid (HCl)aq

• Hydrobromic acid (HBr)aq

• Hydroiodic acid (HI)aq

• Nitric acid (HNO3)aq

• Sulfuric acid (H2SO4)aq

• Carbonic acid (H2CO3)aq

• Phosphoric acid (H3PO4)aq

• Ethanoic acid (CH3COOH)aq

• Benzoic acid (C6H5COOH)s

Common bases:

• Calcium oxide (CaO)s

• Copper (II) oxide (CuO)s

• Sodium hydroxide (NaOH)aq

• Lithium hydroxide (LiOH)aq

• Calcium hydroxide (Ca(OH)2)aq

• Barium hydroxide (Ba(OH)2)aq

• Sodium hydrogen carbonate (NaHCO3)aq

• Sodium carbonate (Na2CO3)aq

• Ammonia (NH3)g

• Ethanamine (CH3CH2NH2)g

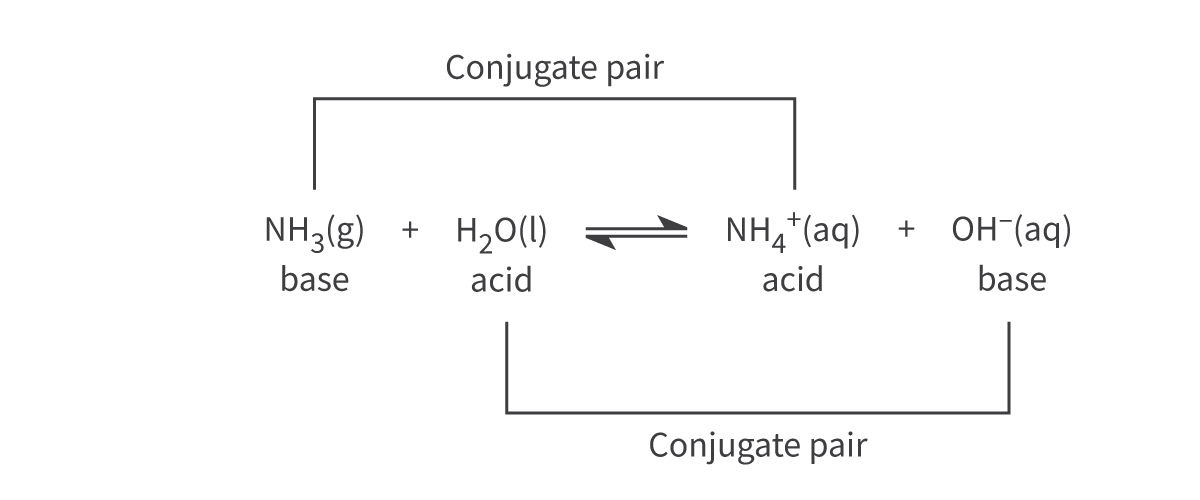
Conjugate acids and bases/Conjugate acid-base pairs: R3.1.2/3

The terms conjugate acid and conjugate base are used to determine the products of an acid base reaction, where:

• Conjugate acids donate a proton in the reverse reaction

• Conjugate bases accept a proton in the reverse reaction

Conjugate acid-base pairs differ by one hydrogen.

Intro to pH calculations (calculations involving proton concentration): R3.1.4/5a

pH is a measure of the concentration of hydrogen ions [H+] in a solution, used to determine how acidic or basic an aqueous solution is.

EQUATION: pH = -log[H+(aq)], where the concentration of H+ is measured in moles per cubic dm. In other words, [H+] = 10^-pH

The greater the [H+], the more acidic the solution. Therefore, the lower the [OH-], the more acidic the solution, as the two values always multiply up to 1×10^14

[H⁺] × [OH⁻] = 1 × 10⁻¹⁴ mol² dm⁻⁶

From the mathematic definition, one can conclude that a change of one pH unit corresponds to 10x the change in hydrogen ion concentration. Therefore, if a solution has a pH of 3, it is 10x more acidic than one with a pH of 4.

Acid-base indicators

Litmus paper and universal indicator are two methods used to determine the pH of a solution. Different indicators turn different colors in acidic or alkaline solutions.

Universal indicator is used alongside indicators to determine the actual pH of a solution, while most other indicators, like litmus paper, can only determine if a solution is acidic or basic.'

Ionic product of Water

The equilibrium constant expression (Kc) for the dissociation of water molecules into H+ and OH- ions is known as the ionic product of water, and has a value of 1×10^-7 mol dm-3 at 298K. At a certain temperature the product of [H+] and [OH-] is constant, meaning if [H+] increases, [OH-] decreases and vice versa.

Strong and Weak Acids and Bases: R3.1.6a

Acids and bases can be classified as strong or weak. The strength of an acid refers to its degree of dissociation (ionisation) in aqueous solution, as strong acids and bases dissociate completely in solution into ions, while weak acids and bases only do so partially.

Complete dissociation is shown using a one way arrow, while partial dissociation is shown using a two way arrow.

The general equations for the dissociation of strong/weak acids are:

• HA(g or l) → H⁺(aq) + A^–(aq)

  • HA(g or l) + H₂O(l) → H₃O⁺(aq) + A^–(aq)

• HA(aq) ⇌ H⁺(aq) + A^–(aq)

  • HA(aq) + H₂O(l) ⇌ H₃O⁺(aq) + A^–(aq)

The general equations for the dissociation of strong/weak bases are:

• MOH(aq) → M⁺(aq) + OH^–(aq)

• B(aq) + H₂O(l) ⇌ BH⁺(aq) + OH^–(aq)

To distinguish between strong and weak acids:

To distinguish between strong and weak bases:

When it comes to the strength of conjugate acids and bases, a general rule of thumb is that strong acids have relatively weak conjugate bases, while weak acids have relatively strong conjugate bases.

The position of equilibrium lies to one side or another depending on the strength of the acid/base. A strong acid ionises more than a weak one, so equilibrium lies to the right. Weak acids have strong conjugate bases, so equilibrium lies to the left. The same goes for bases.

Neutralisation Reactions (Reactions of Acids) - R3.1.7

Neutralisation reactions are reactions between acids and bases, which move the pH of a solution closer to 7, or the middle. Hence the name, neutralisation. Neautralisation reactions are always exothermic, and always produce a salt and water.

This means the general formula is: acid + alkali —> salt + water.

For example: HNO3 (aq) + NaOH (aq) —> NaNO3 (aq) + H2O (l)

However, this formula can differ slightly depending on what bases react with the acids.

Most metal oxides are insoluble in water, but react in the same way as in the general formula with acids to form a salt and water. Because they are insoluble, metal oxides are considered bases, not alkalis.

• 2HCl + CuO —> + CuCl2 + H2O

Carbonates and Hydrogen Carbonates are also considered bases. The one difference between acid-base reactions with metal oxides and these bases is that CO2 is also produced.

• 2HCl + Li2CO3 —> 2LiCl + H2O + CO2

pH Curves for Neutralisation Involving Strong Acid-Base Reactions: R3.1.8

Titrations can be used to measure the acid content of different solutions. An alkali is poured into a burette with an acid in a conical flask. The volume of alkali required to neutralise the reaction measured to find the acid content of the solution in the conical flask.

When neutralisation occurs (the indicator in the conical flask changes the solution’s color), the equivalence point has been reached.

The equivalence point is the point at which a stoichiometric volume of alkali has been reached. When the change in pH of a solution/the titration is graphed, it is shown that there is a rapid change in pH at the equivalence point, or point of inflexion. This is represented by a near-vertical line, and the equivalence point is at the halfway point of this line.

The pOH Scale abd Acid and Base Dissociation Constants: R3.1.9/10

the pOH of a solution is a measurement of the concentration of OH- ions in the solution, and can be used to determine how basic a species is. Its formula is the same as the one for pH, but with [OH-] rather than [H+].

[OH⁻] = 10^−pOH and pOH = -log[OH- (aq)]

[H⁺] × [OH⁻] = 1 × 10⁻¹⁴ mol² dm⁻⁶

Using these formulae, and the ones from pH, we can interconvert between [H+], [OH-], pH, and pOH.

Acid and Base dissociation constants

There exists an equilibrium between the dissociated and undissociated forms of acids and bases (strong and weak forms). The dissociation of a weak acid of weak base has a constant associated with it that tell sus the extent of this dissociation and where the position of equilibrium lies. For weak acids, this is the dissociation constant, Ka.

Ka = [H3O+]x[A-]/[HA], where Ka is the acid dissociation constant in mol dm-3, and [HA] is the concentration of the acid in mol dm-3.

OR

Ka = [H+]x[A-]/[HA] with all values in mol dm-3.

The Ka value is temperature dependent, as it has a fixed value for a particular acid at a particular temperature. Weak acids with higher Ka values are stronger and more dissociated in solution than those with lower Ka values, because the weaker the acid, the less is dissociates, and the lower the product concentration/higher the acid concentration.

The base dissociation constant, Kb, is found using a similar formula, but applied to the concentration of the base, positive base ion, and hydroxide ion concentration in mol dm-3.

Kb = [BH+]x[OH-]/[B]

For weak bases, the reactants are favored, and the weaker the base, the less is dissociates, resulting in a lower product concentration and higher base concentration. Therefore, the Kb value tells us about the strength and therefore the degree of dissociation of a base.

pK_a = –log K_a      and      pK_b = –logK_b

K_a = 10^–pKa       and      K_b = 10^–pKb

^{The stronger the acid, the greater the Ka value and smaller the pKa value. Meanwhile, the stronger the base, the larger the Kb value and the smaller the pKb value.}

^{The Ion Product Constant of Water and the Acid and Base Dissociation Constants: R3.1.11}

^{When calculating pH of strong acids and bases we assume the full dissociation into ions in the solution, which allows us to use the initial concentration of the acid/base to calculate the pH or pOH of the solution. This cannot be done for partially dissociating weak acids/bases, though.}

^{However, this can be worked around by assuming that the number of molecules that dissociated is small enough to be negligible, allowing us to use the equilibrium concentration of the undissociated acid molecules as the initial concentration of the acid. A similar assumption is made for weak bases.}

^{Formulae for conjugate acid-base pairs:}

• K_a × K_b = K_w

• pK_a + pK_b = pK_w

• pK_a + pK_b = 14.00 at 298 K

Reasoning behind these formulae:

• For an acid: HA(aq) + H₂O(l) ⇌ H₃O⁺(aq) + A^–(aq)

  • Ka = [H3O+]x[A-]/[HA]

• For its conjugate base A^–: A^–(aq) + H₂O(l) ⇌ HA(aq) + OH^–(aq)

  • Kb = [OH-]x[HA]/[A-]

If Ka and Kb are multiplied, Ka x Kb = [H3O+]x[OH-] which is equal to Kw, the ionic product of water. This results in the following equation:

Ka x Kb = 1×10-14 mol2 dm-6

By taking the logarithm of both sides, we get pKa + pKb =14, therefore, we can conclude that the stronger the acid and higher its Ka, the lower the Kb of the conjugate base.

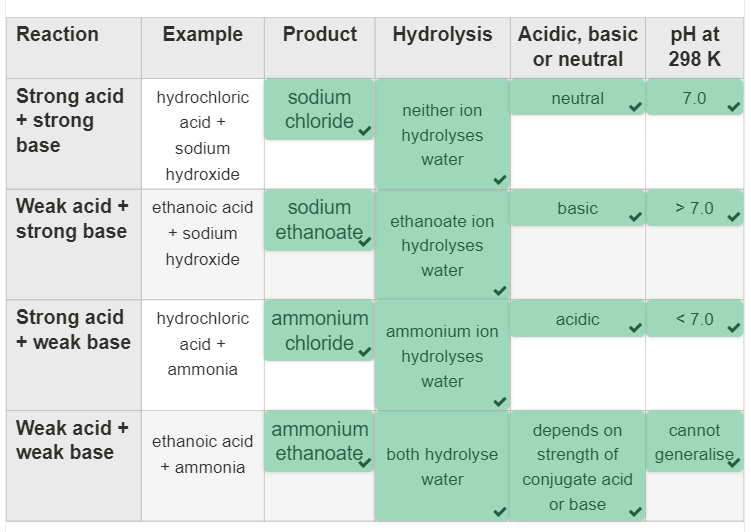
pH of Salt Solutions: R3.1.12

While salts are the product of neutralisation reactions, they don’t all form neutral solutions, as salts can be acidic or basic as well.

When strong acids and bases react together, the salt produced has a pH of 7, however, salts of a combination of strong acids and weak bases, or strong bases and weak acids, have a different result.

Weak acids and strong bases:

Strong bases and weak acids form basic salts. Meaning salts with pH values greater than 7.

Strong acids and weak bases:

Weak bases and strong acids form a salt with a pH less than 7.

Weak acids and weak bases:

pH Curves for Combinations of Strong and Weak Acids and Bases: R3.1.13

Titration curves (graphs) look different for different combinations of acids and bases and their strengths.

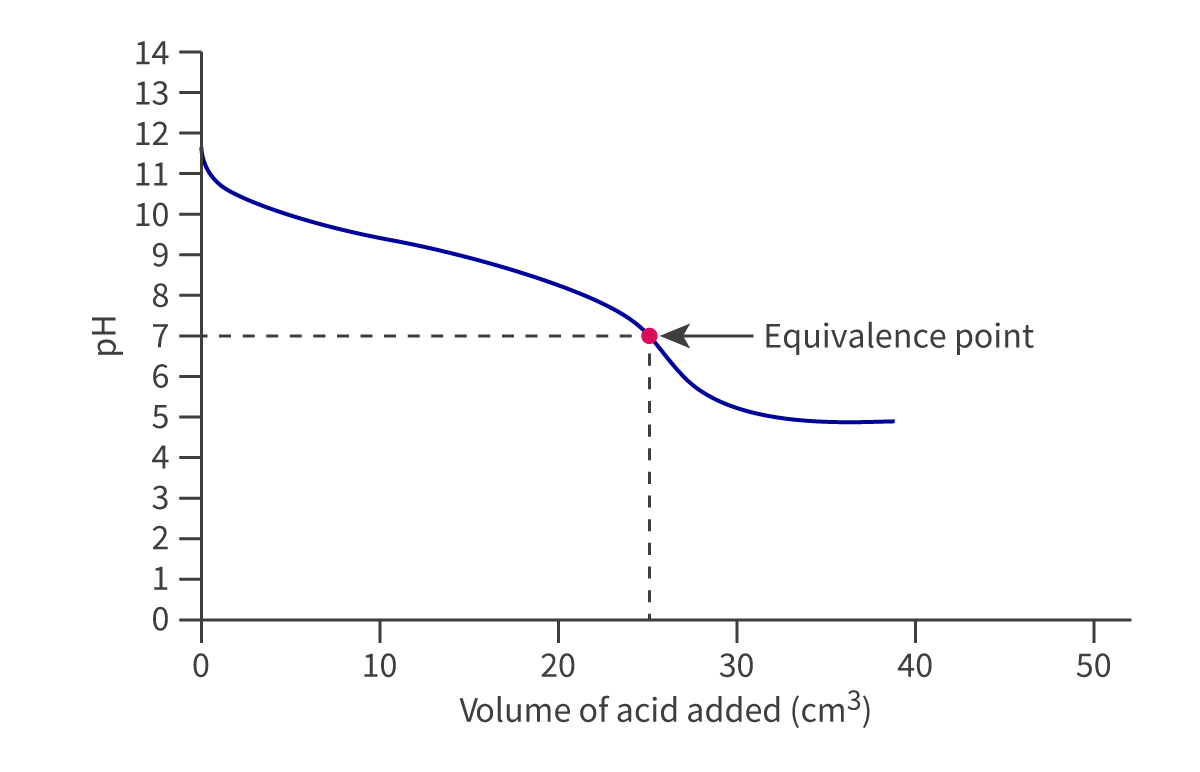
Weak acid-strong base titrations have less dramatic curves like so:

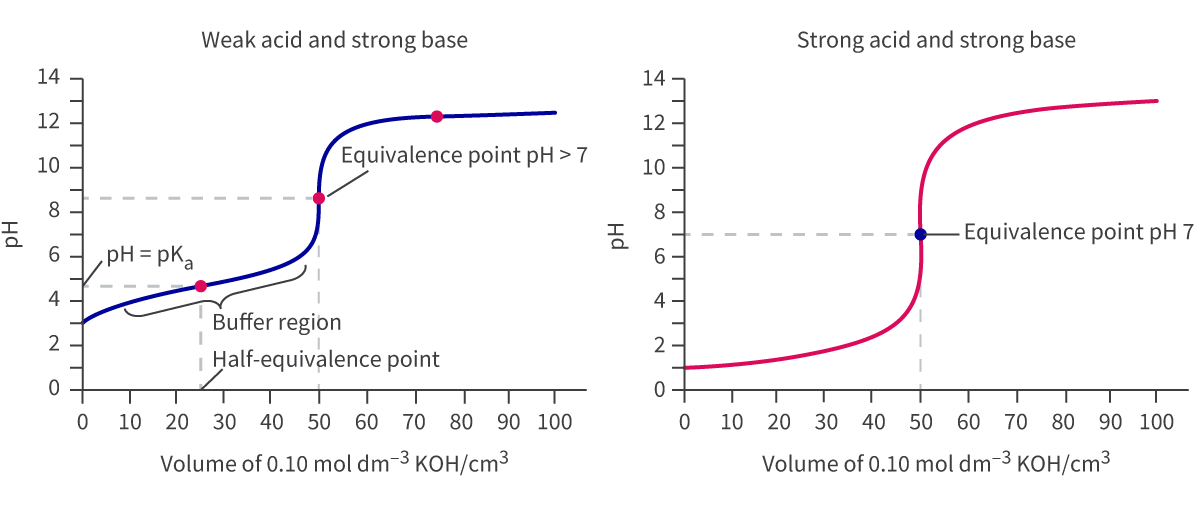
The buffer region is the region on the graph that remains relatively constant. This region is where the solution ocntains the weak acid and a significant amount of the conjugate base.

Buffer solutions’ role is to resist changes in pH on the addition of external acidic or basic solutions. This is called the half-equivalence point. At this point, the pH is equal to the pKa of the acid, and can be read directly from the graph. Additionally, at this pont, the Ka = [H+] and so pKa = pH.

For these curves, the pH at the equivalence point is greater than 7.

Weak base-strong acid titrations have opposite curves to strong base-weak acid titrations and look like this:

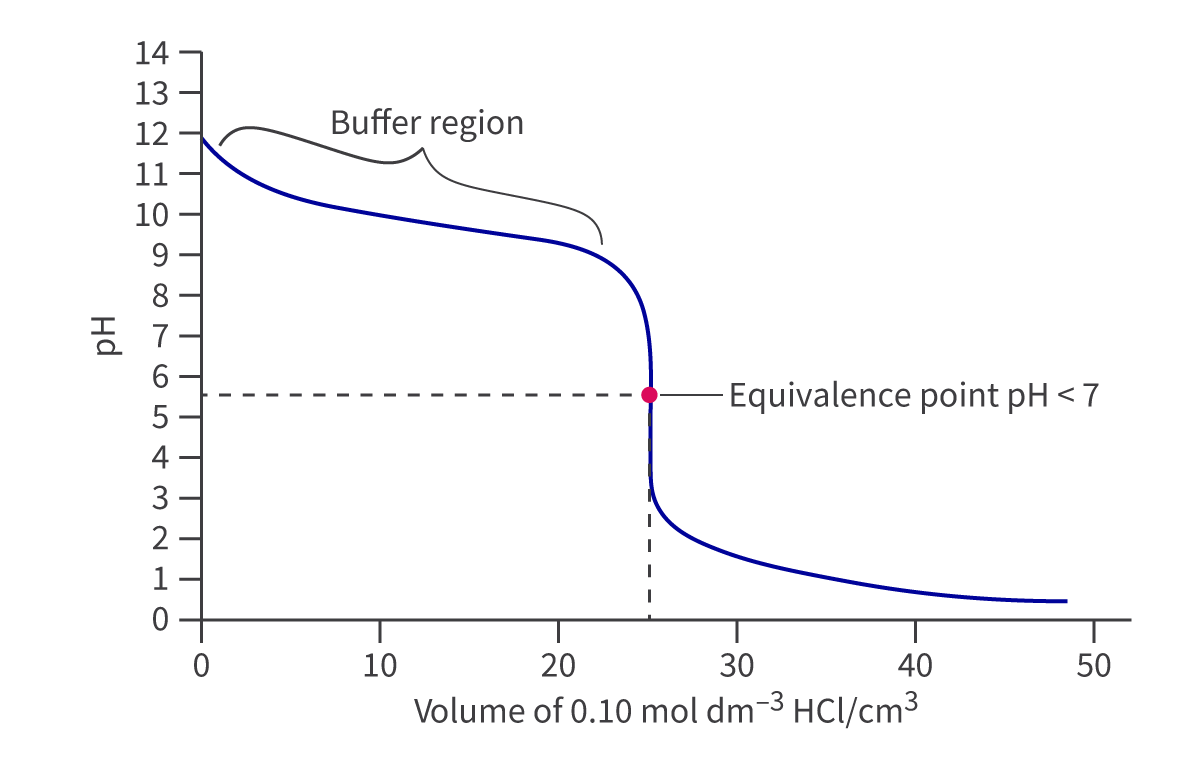
In the buffer region for this curve/titration, at the half-equivalence point, the pH of the conjugate acid of the weak base is equal to pKa, or pOH = pKb for the weak base.

For these curves, pH at the equivalence point is less than 7.

For weak-acid weak-base titrations, the curve is less dramatic, like so:

Acid-base Indicators and Appropriate Indicator Choice: R3.1.14/15

Natural indicators are in foods, and can be used as acid-base indicators. Acid-base indicators are weak acids or bases where the dissociated and undissociated forms have different colors.

These indicators exist in equilibrium between the two forms, represented as HIn and In- in the following equation:

HIn(aq) ⇌ H⁺(aq) + In⁻(aq)
  Colour A         Colour B   

Depending on the concentration of H+ or OH- ions in the solution, the solution will take one color or another. For example, phenolphthalein appears colorless when equilibrium is positioned to the left (increase in H+), and pink when it is positioned to the right (OH- increases).

Indicators change color when their pH=pKa.

Different indicators have different ranges of pH values that they can detect/work in. This can be seen in the formula booklet.

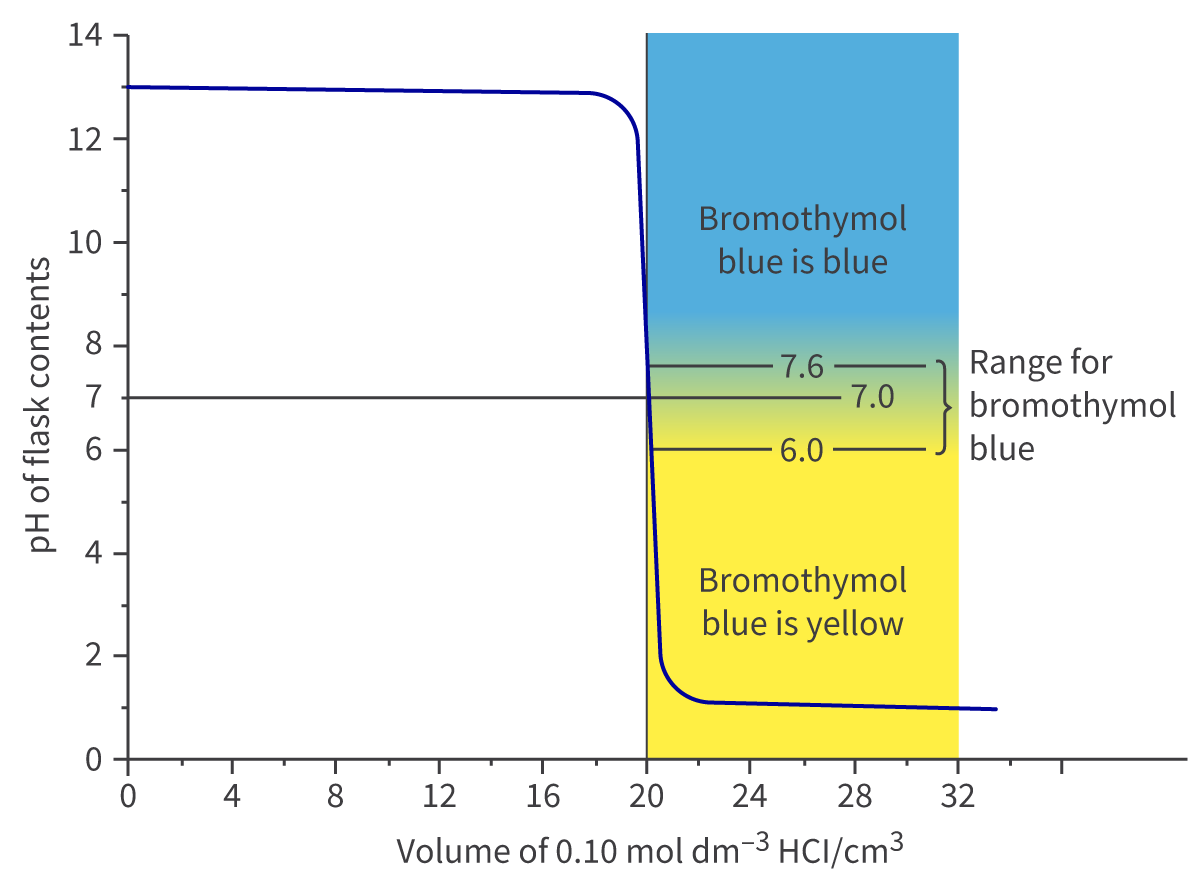
By looking at titration curves for different acid-base combinations, the indicators suitable for use for those can be found. For example, phenolphthalein is appropriate for a titration for a strong base and weak acid, but methyl orange isn’t, because the pH range over which methyl orange changes color doesn’t fall within the vertical region of the curve.

Buffer Solutions: R3.1.16/17

Buffer solutions are used to resist change in pH when acidic or alkaline substances are added, and are utilized when it is necessary to have a controlled pH.

The way this works is that buffer systems shift equilibrium to combat changes in the system. For example, for this system:

H₂CO₃(aq) + H₂O(l) ⇌ HCO₃^–(aq) + H₃O⁺(aq)

If an acidic substance were added, the system would shift equilibrium to the left to favor the reactants, consuming the excess H+ ions. When bases are added, the system would shift to the right to favor the products, producing excess H+ ions to balance the OH- concentration.

Adding very small amounts maintains the pH relatively constant.

Buffer composition

Buffers require a weak acid or base as the primary component to have a system with equilibrium. There are a few methods to make a buffer, using weak acids and bases:

The pH of the buffer is determined by the pKa or pKb of the weak acid or base and the relative ratio of the concentrations of weak acid or base and the conjugate base or acid.

Calculating pH of buffers

The pH of acidic buffers is calculated using the equilibrium expression and Ka or pKa of the weak acid, then using the pH formula.

For basic buffers, you have to find Kb by multiplying both sides of the Kb equation by -log base 10. Then, rearrange the equation to get

pOH = pKb + log10([HB+]/[B]). Then the results can be put into the last equation:

pH = 14-pOH

It is also important to note that while diluted buffer solutions still act as buffers, their ability to resist larger changes in pH lessens. More concentrated buffers shift equilibrium more sufficiently than diluted buffers.