CHEM122 Chemical Kinetics

State and Path Functions

State functions do not depend on how the system arrived at its present state.
A state function describes the equilibrium state of a system.
Path functions depend on how the system went from state 1 to state 2.

Important Concepts for Chem122

Thermodynamics versus kinetics
Kinetic versus thermodynamic products
Average rates - initial method to assess rates of reaction
Instantaneous rates - accurate measurement of reaction rates
Rate laws - stoichiometry at the reaction transition state

Reaction Kinetics

Understanding Reaction Kinetics

Dependence of reaction rate on concentrations: rate laws and equations, how to determine which equation applies.
Reaction mechanisms: equilibrium, explain why rate equations appear as they do.
Temperature dependence of reaction rates: Arrhenius behaviour, activation energy.
Catalysis: speeding up reactions.

Importance of Kinetics and Thermodynamics

Thermodynamics versus kinetics: some reactions are thermodynamically favoured yet occur extremely slowly.
Example: HO• + CH4 → products, the rate constant (k) for this process determines the lifetime of CH4 in the atmosphere (CH4 is a potent greenhouse gas).
Other examples include: atmospheric reactions, ozone depletion, metabolism of drugs, rates of combustion, rates of fermentation to produce alcohol.

Reaction Coordinate and Kinetics

Defining a Reaction Coordinate

Rate of reaction is related to the probability of crossing the energy barrier that separates the reactants from the products.
The highest energy point on the reaction coordinate is called the transition state.

Importance of Chemical Kinetics

Kinetics is the study of the rates for chemical reactions.
Kinetic measurements can be used to provide insight into the mechanism of complex reactions.

Measuring Reaction Rates

Classical Gas Phase Reactions

Consider the reaction: 2NO2(g) → 2NO(g) + O2(g).
If we place 0.01 M of NO2(g) at 573 K (300 °C) in a container and monitor concentrations versus time, we can calculate the rate of the reaction.

Calculating Reaction Rates

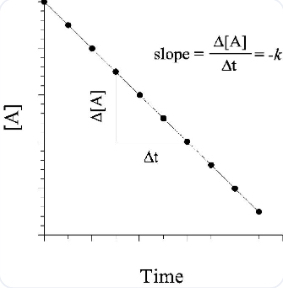
Rate of reaction = ΔA/Δt
Rate of reaction = A at time t2 - A at time t1 / t2 - t1
Rate of reaction = -Δ[NO2]/Δt.

Average Rate of Reaction

Average rates of reaction can change with time.
Example: Average rate of decomposition of nitrogen dioxide as a function of time (Table 15.2).

Instantaneous Rate of Reaction

Instantaneous rate of reaction is the rate at any given point in time (use the tangent to the curve of concentration versus time).
For example, at 100 s, Rate = −Δ[NO2]/Δt = 0.0026, which equals 2.4 × 10^−3 mol L^−1 s^−1.

Monitoring Product Formation

Can measure rates of reaction by monitoring product formation:
Rate of NO production = 2 × rate of O2 production.
Rate of NO2 consumption = rate of NO production = 2 × rate of O2 production.

Determining the Rate Law

Steps to Obtain the Reaction Rate Law

Need a method to measure reaction rates.
Need to know how to write possible rate laws.
How to use reaction rate data to derive the correct rate law.

Reaction Order

Overview of Reaction Orders

What are the reaction orders for the overall reaction?

Types of Reaction Orders

First order rate laws depend on 1 reactant.
Second order rate laws are proportional to [] or product of reactants.
Zero order rate laws occur at constant rates.
Third order rate laws have a super small chance of occurring.

Rate Laws and Their Determination

Differential Rate Law

Reaction rates can be expressed in terms of concentrations: Rate = −d[NO2]/dt = k[NO2]^n, where n = order of reaction and k = proportionality constant.

Generalized Rate Law

For more complicated reactions: A + B → products, rate = k[A]^n[B]^m.
Rate is not necessarily related to stoichiometry.

Method of Initial Rates

Use the method of initial rates to determine the reaction order for more complicated situations.

Integrated Rate Laws

Derivation of Integrated Rate Law

Differential rate law correlates rate as a function of concentration.
Integrated rate law expresses concentration as a function of time.

First Order Rate Law

If k and [N2O5]0 are known, then [N2O5] can be calculated for any time.
If ln[N2O5] is plotted against t, the slope is –k and the intercept is ln[N2O5]0.

Summary of Important Concepts

Summary of the important concepts in reaction rate analyses
integrated rate laws
second order rate laws
zero order rate laws
rate laws – summary and examples
reaction mechanisms
steady-state approximation
![A graph shows the exponential decay of reactant concentration ([A]t) over time.]

Integrated Rate Laws

First Order Rate Processes

first order rate processes: aA products
𝑅𝑎𝑡𝑒= −𝑑𝐴/𝑑𝑡= 𝑘𝐴
(i) rearranging, 𝑑𝐴/𝐴 = −𝑘𝑑𝑡
(ii) integrating: ln 𝐴= −𝑘𝑡+ ln 𝐴଴
first order integrated rate law is an equation for a straight line (y = mx + b) with y = ln[A], x = t, m = –k, b = ln[A]0

Half-Life of First Order Reactions

First order reactions display a characteristic property: an invariant reaction half-life
definition: half-life (n) time taken for concentration to fall to half of its original value
therefore, ln 𝐴଴/𝐴 = 𝑘𝑡 so when 𝐴= 𝐴଴
𝐴଴/𝑘 = 0.693/𝑘
𝑡₁/₂ = ln 2/𝑘
![The equation t_1/2 = [A]₀/2k shows the half-life (t_1/2) of a first-order reaction is equal to the initial concentration ([A]₀) divided by twice the rate constant (k).]

Second Order Reactions

Characteristics of Second Order Reactions

Second order reactions: case A – two identical molecules are present at the transition state
A + A products
𝑅𝑎𝑡𝑒= −𝑑𝐴/𝑑𝑡= 𝑘𝐴²
(i) rearranging 𝑑𝐴/𝐴²= −𝑘𝑑𝑡
(ii) integrating: ∫(1/A²) dA = −∫k dt

Half-Life of Second Order Reactions

Half-life varies with initial concentration for second order reactions
if [A]0 and k are known, [A] can be calculated at any later time
second-order integrated rate law: y = mx + c: has y = 1/[A], x = t, m = k, c = 1/[A]0
half-life: 𝑡₁/₂ = 1/(k[A]0)

Zero Order Reactions

Characteristics of Zero Order Reactions

What happens if reaction rate is independent of a reactant's concentration?
𝑅𝑎𝑡𝑒= −𝑑𝐴/𝑑𝑡= 𝑘𝐴₀= 𝑘
A zero-order reaction has a reaction rate that is independent of concentration
zero-order integrated rate law: y = mx + c with y = [A], x = t, m = –k, c = [A]0

Half-Life of Zero Order Reactions

reaction half-life depends on the initial concentration
𝑡₁/₂ = [A]₀/(2k)

Kinetic Data Collection for Complex Reactions

Pseudo-Rate Laws

How to simplify the collection of kinetic data for complex chemical reactions
for example, a complex reaction such as: aA + bB + cC products
rate = k[A]ⁿ[B]ᵐ[C]ᵖ
we will use pseudo-rate laws (isolation method)

Example of Pseudo-First-Order Rate Constants

An example of the use of pseudo-first-order rate constants
base hydrolysis of ethyl acetate (EtOAc)
use [EtOAc] = 0.001 mol L-1 in 1.0 M NaOH
rate = k'₁[ethyl acetate]
first-order in NaOH and second-order overall

Reaction Mechanisms

Interplay Between Kinetics and Mechanisms

The interplay between reaction kinetics and the reaction mechanism
reactions occur by a series of steps called the reaction mechanism
how do we relate the reaction mechanism to the experimental kinetic data that we have measured?

Elementary Reactions and Rate Laws

Mechanism Composition

The mechanism is composed of a sequence of 'elementary reactions'.
For each reaction step, the rate law for that step is determined by its stoichiometry i.e., its 'molecularity'.
Molecularity is defined by the number of species that are present in the transition state.

Connections Between Reaction Rate Laws and Elementary Steps

Are there connections between the reaction rate laws and its elementary steps?
Elementary Step | Molecularity | Rate Law
A  products | Unimolecular | Rate = k[A]
A + A  products | Bimolecular | Rate = k[A]2
A + B  products | Bimolecular | Rate = k[A][B]
A + A + B  products | Trimolecular | Rate = k[A]2[B]
A + B + C  products | Trimolecular | Rate = k[A][B][C].

Consistency of Reaction Mechanisms with Kinetics

Requirements for Mechanism Consistency

To check a proposed mechanism involving a series of elementary steps, the following two requirements must be satisfied:

1. The sum of the elementary steps must give the overall balanced equation for the reaction.

2. The mechanism must predict the experimentally observed rate law.

Example of Mechanism Consistency

NO2(g) + CO(g)  NO(g) + CO2(g)
The experimentally determined rate law is rate = k[NO2]2.
Suggested mechanism:
k1: NO2 + NO2  NO3 + NO (slow)
k2: NO3 + CO  NO2 + CO2 (fast)
Rate of formation of NO3 = k1[NO2]2.
Overall reaction rate is determined by the slowest (rate-determining) step -- reaction is zero order in CO.

Understanding Complex Reaction Mechanisms

Chain Reactions

Chain reactions exhibit complex kinetics.
Chain reactions often involve radicals (species with an unpaired electron).
These react to produce product and another reactive intermediate.
Typical example: H2 + Cl2  2HCl.

Steps in Chain Reactions

Three important steps:

1. Chain initiation: Cl2 + hv  Cl• + Cl•

2. Chain propagation:

• Step 1: Cl• + H2  HCl + H•

  • Step 2: H• + Cl2  HCl + Cl•

3. Chain termination: Cl• + Cl•  Cl2 or Cl• + H•  HCl.

Steady State Approximation in Rate Equations

Concept of Steady State

If the rate-determining step cannot be identified readily, can use the 'steady state' approximation:
The concentration of a reactive intermediate remains constant as the reaction proceeds.

Application of Steady State Approximation

For the reaction: 2O3(g)  3O2(g)
Proposed mechanism:
Step 2 is rate-determining (or rate-limiting).
Write the rate equation for step 2: Rate = k2[O2][O3], but d[O3]/dt = 0.

Temperature Dependence of Reaction Rates

General Trends

In general, reaction rate constants increase with temperature.
Svante August Arrhenius found experimentally that for many reactions a plot of ln(k) versus 1/T (in Kelvin) gives a straight line.

Activation Energy

In 1889, Arrhenius introduced the concept of activation energy as the critical energy that chemicals need to react.

Data on Reaction Rates at Different Temperatures

Temperature (°C) | k, L mol–1 s–1
25 | 8.8 × 10–5
30 | 1.6 × 10–4
35 | 2.8 × 10–4
40 | 5.0 × 10–4
45 | 8.5 × 10–4
50 | 1.4 × 10–3.

Understanding Catalysis

Reaction Rate and Temperature

How does the reaction rate change with temperature?
Arrhenius behaviour.
Derivation of models from chemical kinetic data.

Arrhenius Equation

Arrhenius noted that for many reactions a plot of ln(k) versus 1/T (in Kelvin) gave a straight line.
ln 𝑘= ln 𝐴−𝐸௔/𝑅𝑇
Y = ln(k), m = –Ea/R, x = 1/T, and c = ln(A).
A is the Arrhenius pre-exponential factor.
Ea is the activation energy.

Activation Energy Effects

Units of Ea are energy/quantity (kJ/mol: kcal/mol: J/molecule).
R is the gas constant: use constant with the same energy & quantity units.
R = 1.38 × 10−23 J K–1 molecule–1; or 1.987 × 10−3 kcal K–1 mol–1; or 8.314 × 10−3 kJ K–1 mol–1.
The larger the value of Ea is the stronger the temperature dependence on the rate constant.

Activation Energy and Reaction Mechanisms

Activation Energy in Reactions

Activation energy for the following reaction: 2BrNO  2NO +Br2.
In this reaction two Br–NO bonds must be broken.
Each bond has a bond dissociation energy of 243 kJ mol−1.
Energy comes from the kinetic energy of colliding molecules.

Transition State Theory

An energy of at least Ea is required for the reaction to occur.
However, that does not mean that it will occur.

Collision Theory and Reaction Rates

Collision Theory Overview

Any theory must account for the following: Arrhenius behaviour and give meaning to Arrhenius parameters.
Simple collision theory: molecules bounce apart (no reaction) when they collide at low speed.

Maxwell-Boltzmann Distribution

Rate of collisions = σc NA [A] [B].
NA = Avogadro's constant (6.02214086 × 10^23 molecules mol−1).
σ is the collision cross-section.
c is the mean speed at which molecules approach each other.

Importance of Catalysts

Fundamental Properties of Catalysts

A CATALYST is a substance that speeds up a chemical reaction without being consumed.
A CATALYST provides an alternative reaction mechanism with a lower activation energy.
A CATALYST does not affect the energy difference (or equilibrium) between products and reactants.
CATALYSTS can be homogeneous (same phase as the reactants) or heterogeneous (different phase).