
6. Colloidal instability, flocculation and rheology of dispersions
Instability in colloidal dispersions
- Sedimentation
- Creaming
- Flocculation (aggregation)
- Ostwald ripening
Sedimentation- Particle density is higher than the density of continuous phase → particles sink
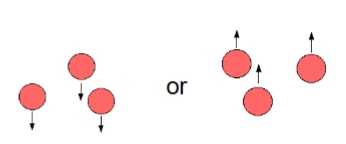
Creaming- Particle density is lower than the density of continuous phase → particles rise to surface
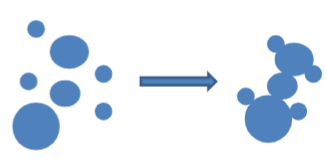
Flocculation (aggregation)- a process where a solute (particles) comes out of solution in the form of floccules due to insufficient repulsion between particles
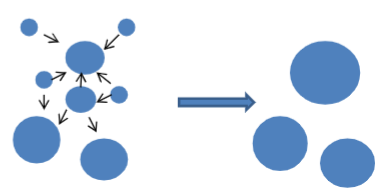
Ostwald ripening- Large particles grow at the expense of smaller ones. Depends on how soluble dispersed phase is in continuous phase
Smaller droplets → higher la place pressure → higher driving force
Sedimentation
Stokes’ law
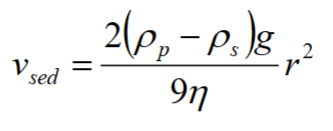
Low concentration (φ<5%): vsed = vStokes
For dispersion by particles is 25%
High concentration: (φ>5%): vsed< vStokes
Sedimentation rates are lower than Stoke’s law predict

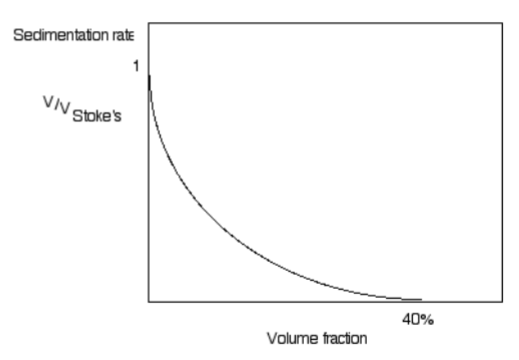
Hindered sedimentation/creaming- The sedimentation or creaming rate decreases with increasing concentration of the dispersed phase.
When we have more 40% sedimentation doesn’t occur since there is no space, the particles are too crowded
Flocculation- depends on properties of surfactants
Mechanisms:
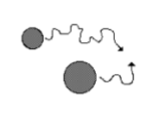
• Brownian motions
The particles get close to each other through random movement
• Shear induced flocculation
Some particles experience higher or lower shear stress depending on their surface
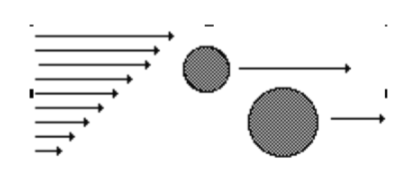
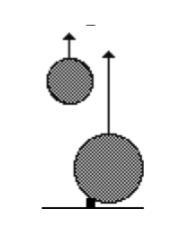
• Gravitity induced flocculation
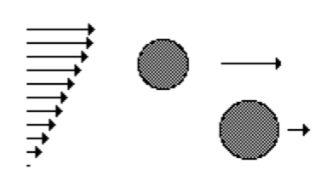
Shear induced flocculation
• Do not include:
• The ”lubricating” properties of the liquids
• The shear sensitivity of the aggregates
• Interactions
• Brownian motions
Comparison between Brownian and shear flocculation rate
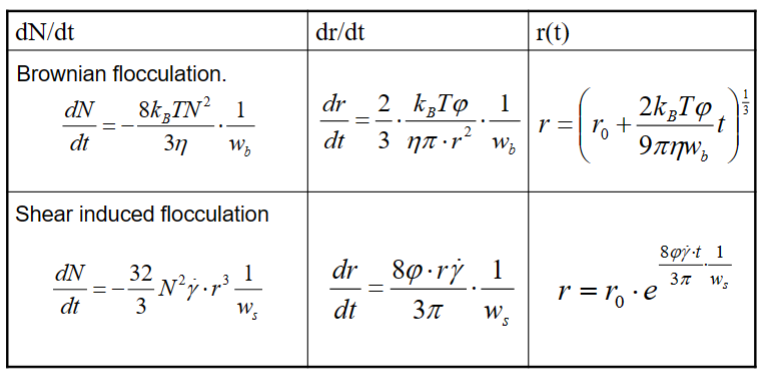
N = number concentration of particles, kB = Boltzmann constant, T = absolute temp., η =
dynamic viscosity, w = stability factor, φ = volume fraction of particles, γ = shear rate
Stability factor
w=1 → each collision leads to aggregation (high possibility of flocculation)
w=106 → one collision in a million leads to aggregation

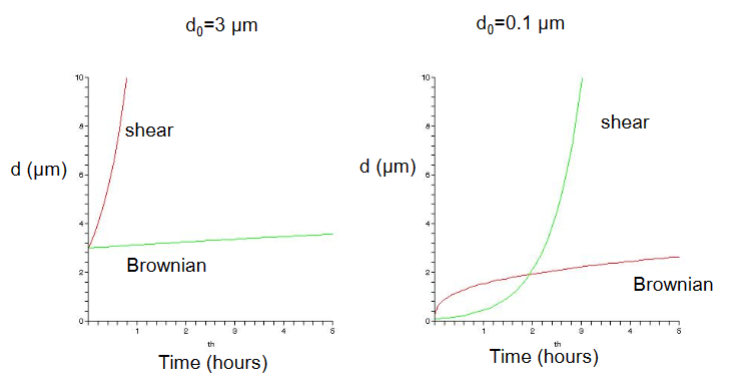
Comparison between shear and Brownian flocculation
do= particle size at time 0
Small particles= flocculation is rapid
do=0.1 μm
Small particles flocculate quickly due to Browian but then it is too big and slow down
Brownian: Initially rapid, but then slowly
Shear: In the beginning, it is slow, but then rapidly increases
do=3 μm
Shear: Rapid growth of particle size. Large and likely to meet than small particles in shear-like movement.
Browian: Slow. Larger particles have a slower diffusion so it takes them longer to randomly meet
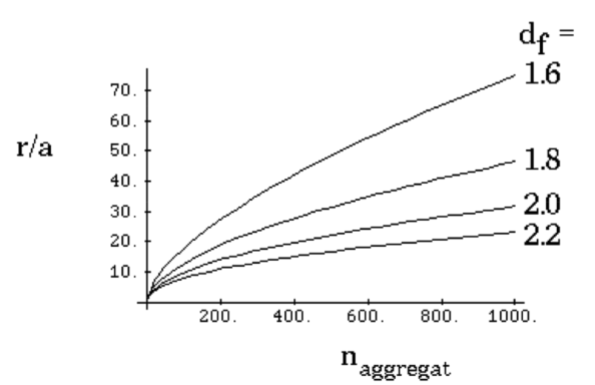
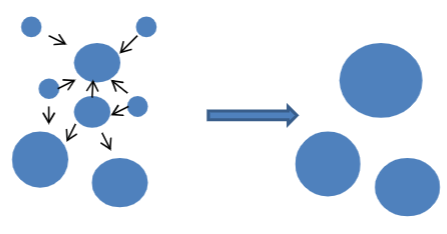
Fractal aggregates (flocs)
• Aggregates that occupy a larger volume than the individual particles are called fractal aggregates or flocs
• The size of the flocs is described by the fractal dimension df
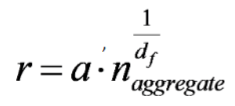
naggregate = the number of particles in the aggregate
a=radius of one particle
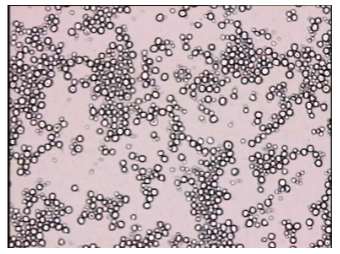
Example of fractal aggregate
• Oil-in-water emulsion produced using membrane emulsification.
Force an oil phase though a membrane with small pores?
Emulsifier not efficient?
Doesn’t give enough repulsion between oil droplets?
Attraction is dominating in the picture below. Loose, string-like structures
Radius of fractal aggregates
The lower the fractal dimension, larger the fractal aggregate radius will be → more continuous phase present?
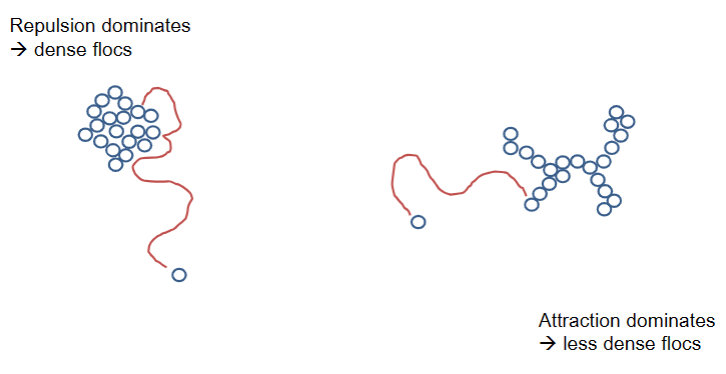
Interactions and aggregate structure
Repulsion dominates → dense flocs
- relatively weak repusion
- Drying - removal of solvent → Forces them together by moving continuous phase
Attraction dominates → less dense flocs
Cheese
Cleared and attraction dominates when pressed
Fractal structure forms as there’s very little control as to what is going on
Like the last slide

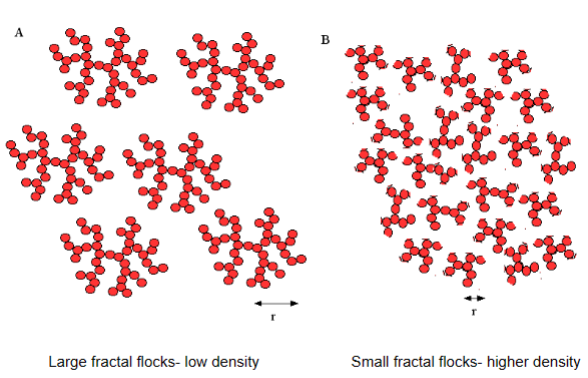
Large fractal flocks - low density
Larger but density lower → more rapid sedimentation
Ostwald ripening
• Driven by the Laplace pressure
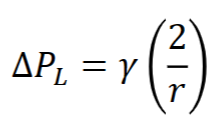
• Molecules from smaller particles dissolve and diffuse to larger particles
• Occurrence and rate also depend on the solubility disperse phase molecules in the continuous phase
– Low solubility slows it down or inhibits it
• Also referred to as ”disproportionation” in foams
We have pressure and high surface tension. We need solubility
If this has low solubility in the continuous phase, process slowed down
Examples
• Waste water treatment.
• Ceramic materials.
• Cheese curd.
Non-Newtonian flow
Non-newtonian behaviour arises from disturbances in the flow pattern caused by sample components
Viscosity decreases as shear rate increases?
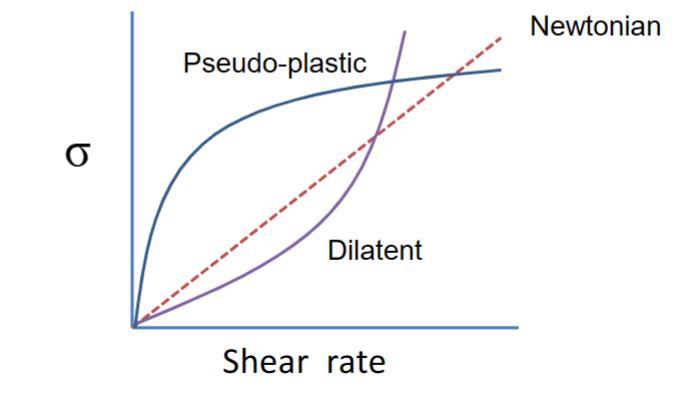
Dispersions commonly display shear-thinning flow beahviour
Orientation of particles in the flow
What happens to the viscosity?
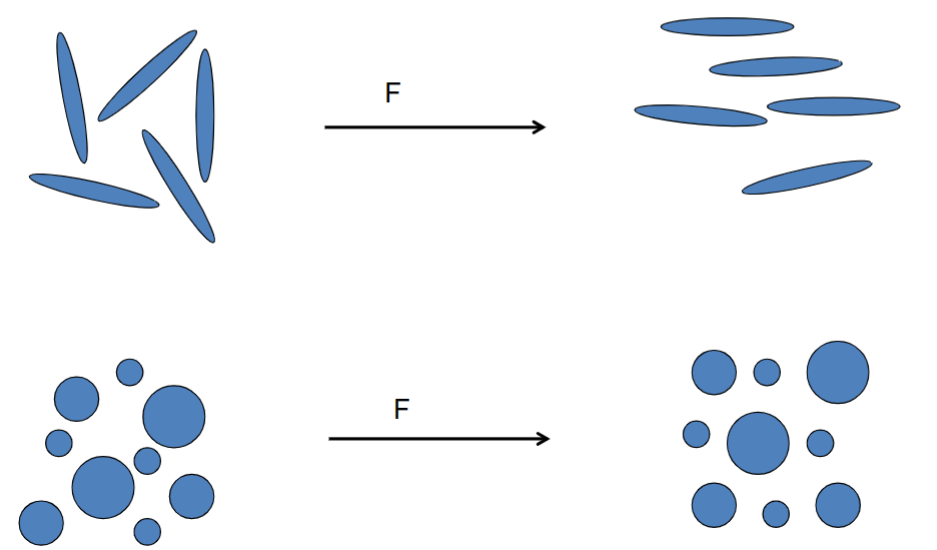
Dispersion rheology
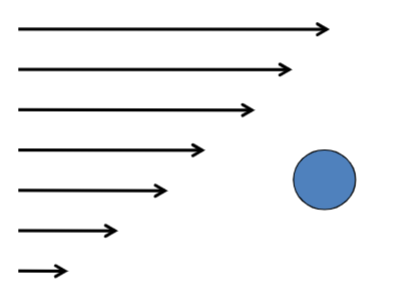
Higher viscosity is the result of particles disturbing the applied flow field and particles ”bumping into each other”.
In pure liquids: viscosity is the result of friction between molecules.
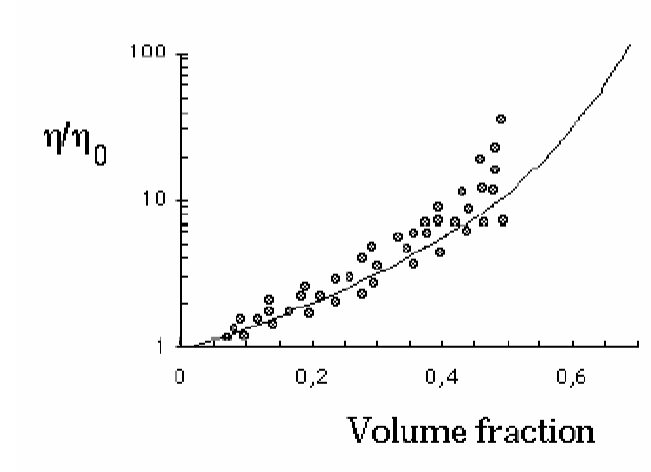
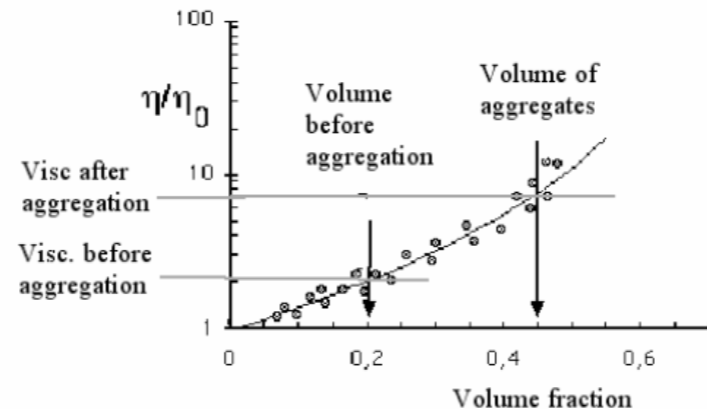
Volume fraction dependence
Relative viscosity vs. volume fraction of particles.
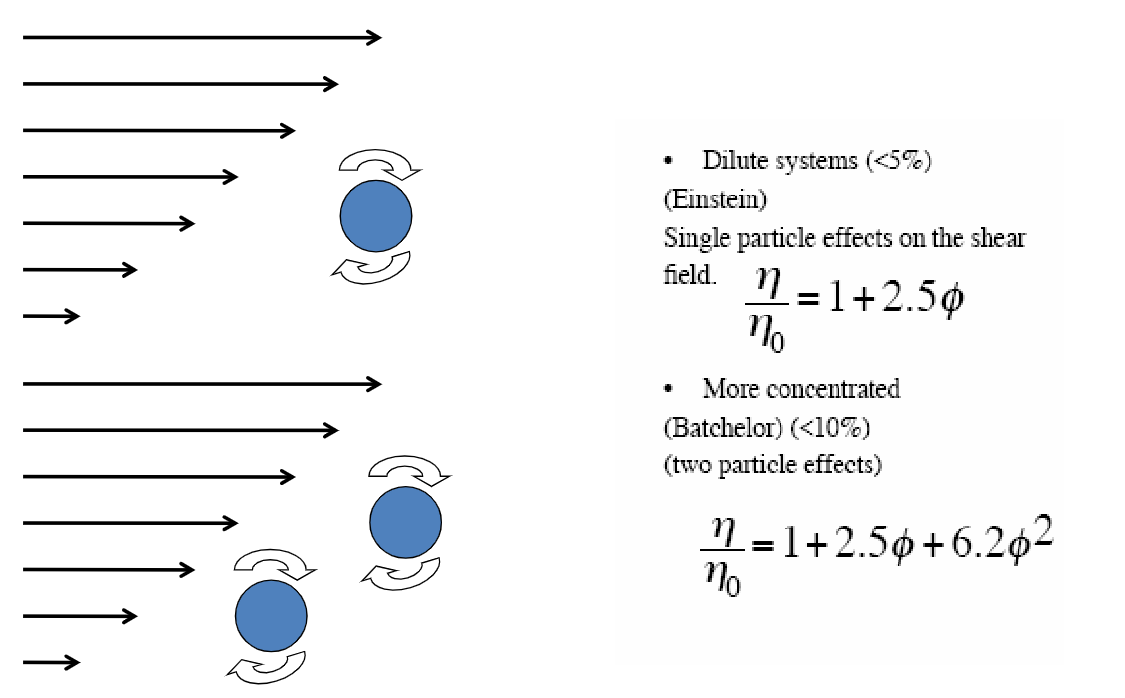
The first is single particle distortion flow
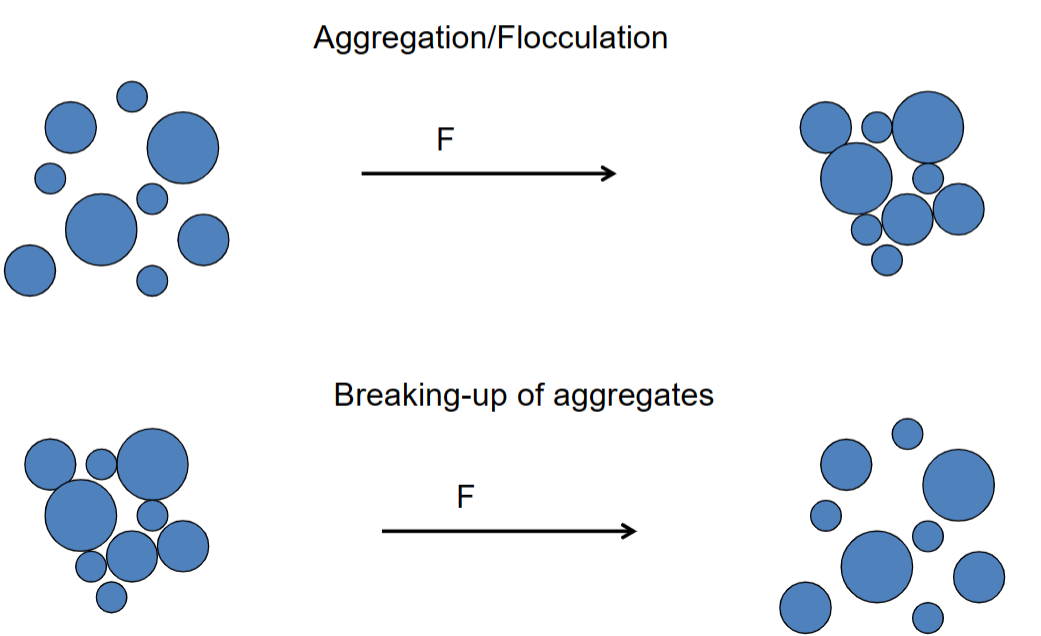
Creation/breaking-up of structures –How does it influence the viscosity?
- Friction between particles
Aggregation/Flocculation:
- Dispersed particles in continuous phase
- Flocculation occurs → Viscosity decreases
Breaking up aggregates:
- More particles flowing around bumping into each other → Viscosity increases
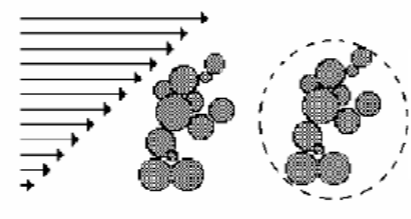
Effects from particle interactions
Repulsive interaction → increase in viscosity (at low shear rates).
Attractive interaction: The effective volume of an aggregate can be larger than the actual aggregate
6. Colloidal instability, flocculation and rheology of dispersions
Instability in colloidal dispersions
- Sedimentation
- Creaming
- Flocculation (aggregation)
- Ostwald ripening
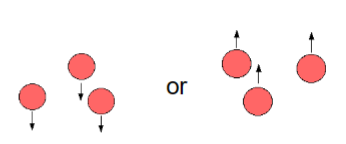
Sedimentation- Particle density is higher than the density of continuous phase → particles sink

Creaming- Particle density is lower than the density of continuous phase → particles rise to surface

Flocculation (aggregation)- a process where a solute (particles) comes out of solution in the form of floccules due to insufficient repulsion between particles

Ostwald ripening- Large particles grow at the expense of smaller ones. Depends on how soluble dispersed phase is in continuous phase
Smaller droplets → higher la place pressure → higher driving force

Sedimentation
Stokes’ law
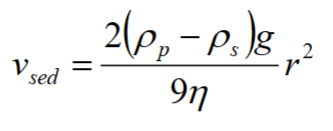
Low concentration (φ<5%): vsed = vStokes
For dispersion by particles is 25%

High concentration: (φ>5%): vsed< vStokes
Sedimentation rates are lower than Stoke’s law predict

Hindered sedimentation/creaming- The sedimentation or creaming rate decreases with increasing concentration of the dispersed phase.
When we have more 40% sedimentation doesn’t occur since there is no space, the particles are too crowded

Flocculation- depends on properties of surfactants
Mechanisms:
• Brownian motions
The particles get close to each other through random movement

• Shear induced flocculation
Some particles experience higher or lower shear stress depending on their surface

• Gravitity induced flocculation

Shear induced flocculation
• Do not include:
• The ”lubricating” properties of the liquids
• The shear sensitivity of the aggregates
• Interactions
• Brownian motions

Comparison between Brownian and shear flocculation rate

N = number concentration of particles, kB = Boltzmann constant, T = absolute temp., η =
dynamic viscosity, w = stability factor, φ = volume fraction of particles, γ = shear rate
Stability factor
w=1 → each collision leads to aggregation (high possibility of flocculation)
w=106 → one collision in a million leads to aggregation

Comparison between shear and Brownian flocculation
do= particle size at time 0
Small particles= flocculation is rapid
do=0.1 μm
Small particles flocculate quickly due to Browian but then it is too big and slow down
Brownian: Initially rapid, but then slowly
Shear: In the beginning, it is slow, but then rapidly increases
do=3 μm
Shear: Rapid growth of particle size. Large and likely to meet than small particles in shear-like movement.
Browian: Slow. Larger particles have a slower diffusion so it takes them longer to randomly meet

Fractal aggregates (flocs)
• Aggregates that occupy a larger volume than the individual particles are called fractal aggregates or flocs
• The size of the flocs is described by the fractal dimension df
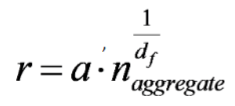
naggregate = the number of particles in the aggregate
a=radius of one particle

Example of fractal aggregate
• Oil-in-water emulsion produced using membrane emulsification.
Force an oil phase though a membrane with small pores?
Emulsifier not efficient?
Doesn’t give enough repulsion between oil droplets?
Attraction is dominating in the picture below. Loose, string-like structures

Radius of fractal aggregates
The lower the fractal dimension, larger the fractal aggregate radius will be → more continuous phase present?

Interactions and aggregate structure
Repulsion dominates → dense flocs
- relatively weak repusion
- Drying - removal of solvent → Forces them together by moving continuous phase
Attraction dominates → less dense flocs
Cheese
Cleared and attraction dominates when pressed
Fractal structure forms as there’s very little control as to what is going on
Like the last slide



Large fractal flocks - low density
Larger but density lower → more rapid sedimentation
Ostwald ripening
• Driven by the Laplace pressure
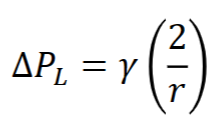
• Molecules from smaller particles dissolve and diffuse to larger particles
• Occurrence and rate also depend on the solubility disperse phase molecules in the continuous phase
– Low solubility slows it down or inhibits it
• Also referred to as ”disproportionation” in foams
We have pressure and high surface tension. We need solubility
If this has low solubility in the continuous phase, process slowed down

Examples
• Waste water treatment.
• Ceramic materials.
• Cheese curd.
Non-Newtonian flow
Non-newtonian behaviour arises from disturbances in the flow pattern caused by sample components
Viscosity decreases as shear rate increases?

Dispersions commonly display shear-thinning flow beahviour
Orientation of particles in the flow
What happens to the viscosity?

Dispersion rheology
Higher viscosity is the result of particles disturbing the applied flow field and particles ”bumping into each other”.
In pure liquids: viscosity is the result of friction between molecules.

Volume fraction dependence
Relative viscosity vs. volume fraction of particles.

The first is single particle distortion flow

Creation/breaking-up of structures –How does it influence the viscosity?
- Friction between particles
Aggregation/Flocculation:
- Dispersed particles in continuous phase
- Flocculation occurs → Viscosity decreases
Breaking up aggregates:
- More particles flowing around bumping into each other → Viscosity increases

Effects from particle interactions
Repulsive interaction → increase in viscosity (at low shear rates).
Attractive interaction: The effective volume of an aggregate can be larger than the actual aggregate

