1. Absolute Maximum and Absolute Minimum

• Absolute Maximum: The highest point on the entire graph of a function within its domain.

  • Found by evaluating the function at critical points and endpoints of the interval.

  • Example: For f(x)=−x2+4x+1f(x) = -x^2 + 4x + 1f(x)=−x2+4x+1, the absolute maximum is the highest value of f(x)f(x)f(x) on a given interval.

• Absolute Minimum: The lowest point on the graph of a function within its domain.

  • Like the absolute maximum, it’s found by checking critical points and endpoints.

  • Example: For f(x)=x2−4x+5f(x) = x^2 - 4x + 5f(x)=x2−4x+5, the absolute minimum is the lowest value of f(x)f(x)f(x) on a given interval.

2. Local Maximum and Local Minimum

• Local Maximum: A point on the graph where the function has a higher value than at any nearby points.

  • Occurs at critical points where the function changes from increasing to decreasing.

  • Example: If f(x)f(x)f(x) has a peak at x=cx = cx=c and is higher than points around it, then f(c)f(c)f(c) is a local maximum.

• Local Minimum: A point where the function has a lower value than any nearby points.

  • Occurs at critical points where the function changes from decreasing to increasing.

  • Example: If f(x)f(x)f(x) has a low point at x=dx = dx=d, f(d)f(d)f(d) is a local minimum.

3. X-Intercepts and Y-Intercept

• X-Intercept(s): The points where the graph crosses the x-axis (where y=0).

  • Found by setting f(x)=0 and solving for x

  • Example: For f(x)=x2−4f(x) = x^2 - 4f(x)=x2−4, the x-intercepts are x=−2x = -2x=−2 and x=2x = 2x=2 (points (−2,0)(-2, 0)(−2,0) and (2,0)(2, 0)(2,0)).

• Y-Intercept: The point where the graph crosses the y-axis (where x=0x = 0x=0).

  • Found by evaluating f(0)f(0)f(0).

  • Example: For f(x)=x2−4x+3f(x) = x^2 - 4x + 3f(x)=x2−4x+3, substitute x=0x = 0x=0 to find the y-intercept as f(0)=3f(0) = 3f(0)=3, so the y-intercept is (0,3)(0, 3)(0,3).

4. Interval of Increase and Interval of Decrease

• Interval of Increase: Where the function values are rising as x moves rightward.

  • Identified by finding intervals where f′(x)>0f'(x) > 0f′(x)>0 (the derivative is positive).

  • Example: For f(x)=x2−4x+5f(x) = x^2 - 4x + 5f(x)=x2−4x+5, f(x)f(x)f(x) increases on intervals where f′(x)f'(x)f′(x) is positive.

• Interval of Decrease: Where the function values are falling as x moves rightward.

  • Found by identifying intervals where f′(x)<0f'(x) < 0f′(x)<0 (the derivative is negative).

  • Example: For f(x)=−x2+4xf(x) = -x^2 + 4xf(x)=−x2+4x, f(x)f(x)f(x) decreases on intervals where f′(x)f'(x)f′(x) is negative.

5. Constant Interval

• Constant Interval: An interval where the function remains the same (flat) and does not increase or decrease.

  • On this interval, f′(x)=0f'(x) = 0f′(x)=0.

  • Example: If f(x)=3f(x) = 3f(x)=3 for all xxx in [−2,2][-2, 2][−2,2], then f(x)f(x)f(x) is constant on [−2,2][-2, 2][−2,2].

6. Even and Odd Functions

Understanding Odd and Even Functions

• Even Function: A function f(x) is even if f(−x)=f(x) for all x in its domain. The graph of an even function is symmetric with respect to the y-axis.

• Odd Function: A function f(x) is odd if f(−x)=−f(x) for all x in its domain. The graph of an odd function is symmetric with respect to the origin.

Identifying Even Functions on a Graph

• Y-Axis Symmetry: For a function to be even, the graph should look the same on both sides of the y-axis.

• Examples of Even Functions:

  • y=x2y = x^2y=x2

  • y=cos⁡(x)y = \cos(x)y=cos(x)

• Graph Check: Fold the graph along the y-axis. If the left side matches the right side perfectly, the function is even.

Identifying Even Functions on a Graph

• Origin Symmetry: An odd function's graph will appear symmetric if rotated 180 degrees around the origin.

• Examples of Odd Functions:

  • y=x3y = x^3y=x3

  • y=sin⁡(x)y = \sin(x)y=sin(x)

• Graph Check: If you can rotate the graph 180° around the origin and it looks the same, the function is odd.

  Steps to Analyze the Graph for Symmetry

1. Y-Axis Symmetry (Even Test):

   • Check if the function is mirrored across the y-axis.

   • If yes, it’s even; if not, move to the next test.

2. Origin Symmetry (Odd Test):

   • Visualize rotating the graph 180 degrees around the origin.

   • If it matches itself after this rotation, it’s odd.

3. Neither Odd Nor Even:

   • Some functions are neither odd nor even if they don’t fit either symmetry. For instance, f(x)=x+1f(x) = x + 1f(x)=x+1.

7. Parent Functions

Constant Function

• Equation: f(x)=cf(x) = cf(x)=c, where ccc is a constant (e.g., f(x)=3f(x) = 3f(x)=3)

• Graph Shape: Horizontal line

• Key Characteristics:

  • Even function (y-axis symmetry).

  • The output value is the same for all xxx.

  • Domain: All real numbers; Range: The constant value ccc.

Linear Function

• Equation: f(x)=xf(x) = xf(x)=x

• Graph Shape: Straight line through the origin

• Key Characteristics:

  • Slope is constant.

  • Odd function (origin symmetry).

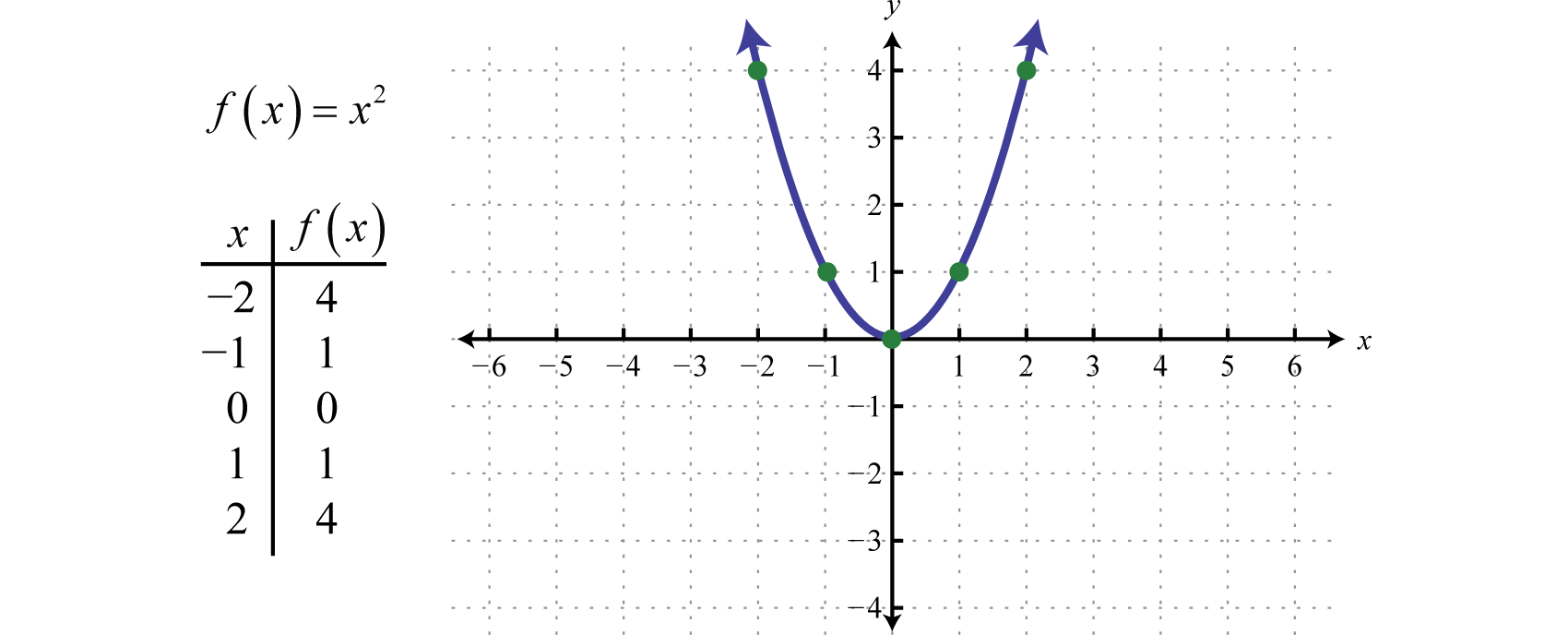
Quadratic Function

• Equation: f(x)=x2f(x) = x^2f(x)=x2

• Graph Shape: Parabola opening upward

• Key Characteristics:

  • Even function (y-axis symmetry).

  • The lowest point is the vertex at the origin.

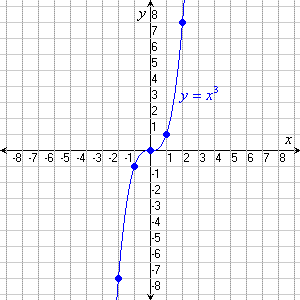
Cubic Function

• Equation: f(x)=x3f(x) = x^3f(x)=x3

• Graph Shape: S-shaped curve, passing through the origin

• Key Characteristics:

  • Odd function (origin symmetry).

  • Increases on both sides of the origin with an inflection point at (0,0).

Square Root Function

• Equation: f(x)=xf(x) = \sqrt{x}f(x)=x​

• Graph Shape: Curve starting at the origin, increasing slowly

• Key Characteristics:

  • Defined only for x≥0x \geq 0x≥0.

  • Increases at a decreasing rate.

Cube Root Function

• Equation: f(x)=x3f(x) = \sqrt[3]{x}f(x)=3x​ or f(x)=x1/3f(x) = x^{1/3}f(x)=x1/3

• Graph Shape: Similar to the cubic function but more gradual, passing through the origin

• Key Characteristics:

  • Odd function (origin symmetry).

  • Defined for all real numbers.

  • Increases slowly for positive xxx and decreases for negative xxx.

Absolute Value Function

• Equation: f(x)=∣x∣ f(x) = |x|f(x)=∣x∣

• Graph Shape: V-shaped, opening upward with a vertex at the origin

• Key Characteristics:

  • Even function (y-axis symmetry).

  • Reflects positive and negative values of xxx into positive f(x)f(x)f(x) values.

Reciprocal Function

• Equation: f(x)=1xf(x) = \frac{1}{x}f(x)=x1​

• Graph Shape: Hyperbolic, with asymptotes along the x- and y-axes

• Key Characteristics:

  • Odd function (origin symmetry).

  • Undefined at x=0x = 0x=0; has vertical and horizontal asymptotes.