OLI - 2. Syntax and symbolization
Atomic Formulae and Logical Connectives
- Two categories:
- Atomic formulae: sentences with no logically relevant internal structure. They don't contain a connector.
- Logical connectives: they serve to connect formulae in order to create new and more complex formulae. They correspond to logical operators.
- Conjunction: and
- Disjunction: or
- Conditional: if… then…
- Negation: not
- The logical connectives represent logical idealizations of the corresponding words in English.
- Logical operators are truth-functional.
- A non-atomic sentence is called a logically compound sentence, it contains atomic sentences and logical operators.
Conjunction
- "And"
- Represented by & or ∧
- Two atomic sentences connected by a conjunction are called conjuncts.
- A single capital letter represents each conjunct.
- It is traditional (and purely conventional) to pick a letter that has some relationship to the corresponding sentence.
- (J & M)
- They must be placed inside parenthesis.
- Types of conjunctions:
- Non-sentential conjunctions: paraphrase two sentences that are joined in order to recognize the conjunctions.
- The cat nd the dog have been fed - The cat has been fed and the dog has been fed
- Non-truth-functional conjunction: even if we paraphrase the two sentences, they don't make sense on their own, so the atomic sentence is the whole sentence.
- Vanilla ice cream and chocolate syrup make a great sundae - Vanilla ice cream makes a great sundae and chocolate syrup makes a great sundae.
- Not-just-truth-functional conjunction: the symbolizations only capture part of the overall meaning of the sentence. If the order is changed, the meaning (but not the truth-value) changes.
- The villain jumped on the train and the villain yelled - The villain yelled and the villain jumped on the train.
- Conjuncts can be joined by other words than "and"
- Mary likes dogs, whereas John likes cats - Mary likes dogs and John likes cats.
- &-introduction: adding the ampersand to two conjuncts.
Disjunction
- "or"
- Represented by ∨
- The two atomic sentences joined by a disjunction are called disjuncts.
- (J∨M)
- Types of disjunctions
- Non-sentential disjunction: paraphrase two sentences that are joined in order to recognize the disjunts.
- Either John or Mary laughed - Either John laughed, or Mary laughed.
- Disjunction is always truth-functional: the paraphrase does have the same meaning as the original sentence, even though the original sentence is obviously false.
- Ambiguity of disjunction: there can be an inclusive (one but not both) or an exclusive (true if only one of them is, false if both are true) interpretation.
- Disjunctions will only use "or", and sometimes "either… or…"
Conditional
- "If… then…"
- Represented by →
- Connects two sentential clauses to form a conditional sentence.
- (J→M)
- The "if" clause is called the antecedent, the "then" clause is called the consequent.
- →-elimination or modus ponens
- If we know that a conditional is true, and its antecedent is as well, then we can infer the truth of the consequent.
Negation
- "Not"
- Represented by ~ or ¬
- ¬J
- Negation is a unary connective, as it only connects one formula, while the other connectives are binary.
- Types of negation:
- Non-sentential negations: the word "not" doesn't appear explicitly.
- The cat is unhappy - The cat is not happy - It is not the case that the cat is happy
- Non-truth-functional negatives: when we can't remove the prefix.
- The cat is disturbed.
Combination of connectives
- Main connective: the top-level structure of the sentence.
- (D∨(F&G))
- The main connective here is a disjunction.
- The scope, or the influence, of the connector is contained within the parenthesis.
- Scope of the conjunction: (F&G)
- Scope of the disjunction: (D∨(F&G))
- We paraphrase sentences to reformulate them.
- If Bob gathers eggs, then either he won't feed the chickens or he won't feed the ducks.
- (G→(¬C∨¬D))
- Sometimes, a sentence will be ambiguous and it is impossible to tell what the structure should be.
- It will rain and it will hail or it will snow.
- Which can be ((R&H)vO) or (R&(HvO)).
- The word unless can also be hard to interpret.
Formal syntax
- Basic symbols of sentential logic
- The capital letters we use to symbolize atomic sentences, called atomic formulae or occasionally sentential letters: A, B, C, and so on (possibly with numeric subscripts).
- The symbols for the logical connectives: &, ∨, →, and ¬.
- The parentheses used to disambiguate the scope of the connectives: ( and ).
- Expressions of sentential logic
- Any finite sequence or string of basic symbols is an expression of sentential logic.
- We can use variables to range over expressions and not mistake them for sentential letters.
- Formulae (rules) of sentential logic
- Every atomic formula φ is a formula of sentential logic.
- If φ is a formula of sentential logic, then so is ¬φ.
- If φ and ψ are formulae of sentential logic, then so are each of the following:
- (φ&ψ)
- (φ∨ψ)
- (φ→ψ)
- An expression φ of sentential logic is a formula only if it can be constructed by finitely many applications of the first three rules.
Parse trees
A parse tree graphically represents the internal structure of an expression of sentential logic.
- It helps to test whether or not the expression is well-formed.
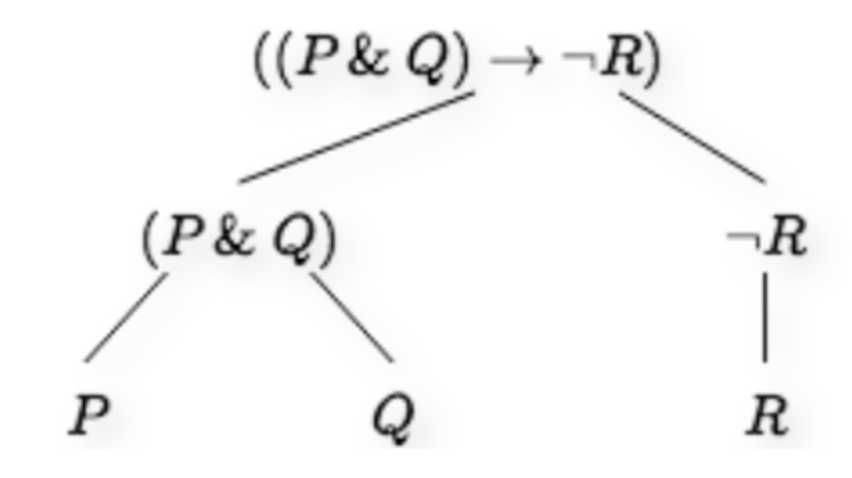
- It helps to test whether or not the expression is well-formed.
Steps to construct a parse tree
- Write down the entire expression. It must only contain basic symbols.
- Identify the general form of the expresion.
- A sentential letter
- A negation symbol followed by a subexpression
- A conjunction (φ&ψ).
- A disjunction (φ∨ψ).
- A conditional (φ→ψ).
- Find the top-level structure.
- Ignore everything inside the embedded parenthesis
- ((P∨Q)&¬(R→S)) can be seen as (()&¬()).
- If it appears to have multiple top-level structures, it is not well-formed.
- (()&∨())
- Create a branch for each subexpression.
- Continue until each branch ends in a sentential letter.
Subformula: a formula ψ is a subformula of a formula φ if and only if ψ appears (as a node) in the parse tree of φ.
Conventions
A convention governs a practice of doing something in one particular way, if that practice could have been done another way and still achieve its implicit goal.
- For example, & represents a conjunction, but it could have been ∧
Procedure for reinserting omittes parenthesis
- 1First, insert parentheses around every occurrence of & and its two conjuncts, starting with the rightmost & and ending with the leftmost,
- Next, insert parentheses in the same fashion for each ∨ and its two disjuncts, from rightmost occurrence first, to the leftmost occurrence last,
- Finally, insert parentheses for each →, and its antecedent and consequent, from rightmost occurrence first, to the leftmost occurrence last.
- Parentheses are never inserted around negations
- You should never break up existing pairs of parentheses.
Summary
- The building blocks of the language are atomic formulae and logical connectives. Atomic formulae or sentential letters are capital letters used to represent logically simple sentences.
- The logical connectives, conjunction, disjunction, the conditional, and negation, serve to join sentences together to create logically compound formulae.
- Conjunction is the connective that corresponds to the word ‘and’.
- Disjunction is the connective that corresponds to the word ‘or’.
- The conditional is the connective that corresponds to the phrase ‘if…then…’.
- Negation is the connective that corresponds to the word ‘not’.
- More complicated sentences and combinations of connectives are considered.
- The formal rules that define the syntax of sentential logic are presented.
- The notion of a parse tree is introduced, and a procedure for constructing a parse tree is provided that allow us to decide (in finitely many steps) whether or not an expression is a formula.
- Syntactic conventions, including choices of symbols and omission of parentheses, are discussed.
Must-know definitions
- Basic symbols of sentential logic
- Expressions of sentential logic
- Formulae of sentential logic
- Parse tree construction rules
- Subformula
- Procedure for reinserting omitted parenthesis
New terms
| atomic formulae | logical connectives | conjunction | disjunction | conditional |
|---|---|---|---|---|
| negation | logical operators | idealizations | compound | truth-functional |
| semantics | meaning | truth-values | compound sentence | compound formula |
| symbolize | translate | conjuncts | disjuncts | inclusive |
| exclusive | conditional | antecedent | consequent | unary |
| binary | main connective | scope | ambiguous | basic symbols |
| formula | expression | well-formed formula | formula | variables |
| inductive | semantics | parse tree | subformula |