What to include when solving problems

• Reference frame

• Picture

• List given variables

• List what you need to find

• Pure equations (no substitutions)

• Step by step solutions

• Units

• Show unit cancelations

Variables

Units Prefixes to Denote Multiples of Ten

• 1 megameter = 1000000 m

• 1 kilometer = 1000 m

• 1 centimeter = 0.01 m

• 1 millimeter = 0.001 m

• 1 micrometer = 0.000001 m

• 1 nanometer = 0.000000001 m

Converting Units

SI Units

• Meters

• Kilograms

• Seconds

Other conversions

• 1 mile = 1609.34 meters =5280 ft = 1.60934 km

• 1 meter = 3.281 ft

• 1 inch = 2.54 cm

• 1 hour = 3600 s

• 1 kilometer = 1000 m

Chapter 1: Introduction and Mathematical Concepts

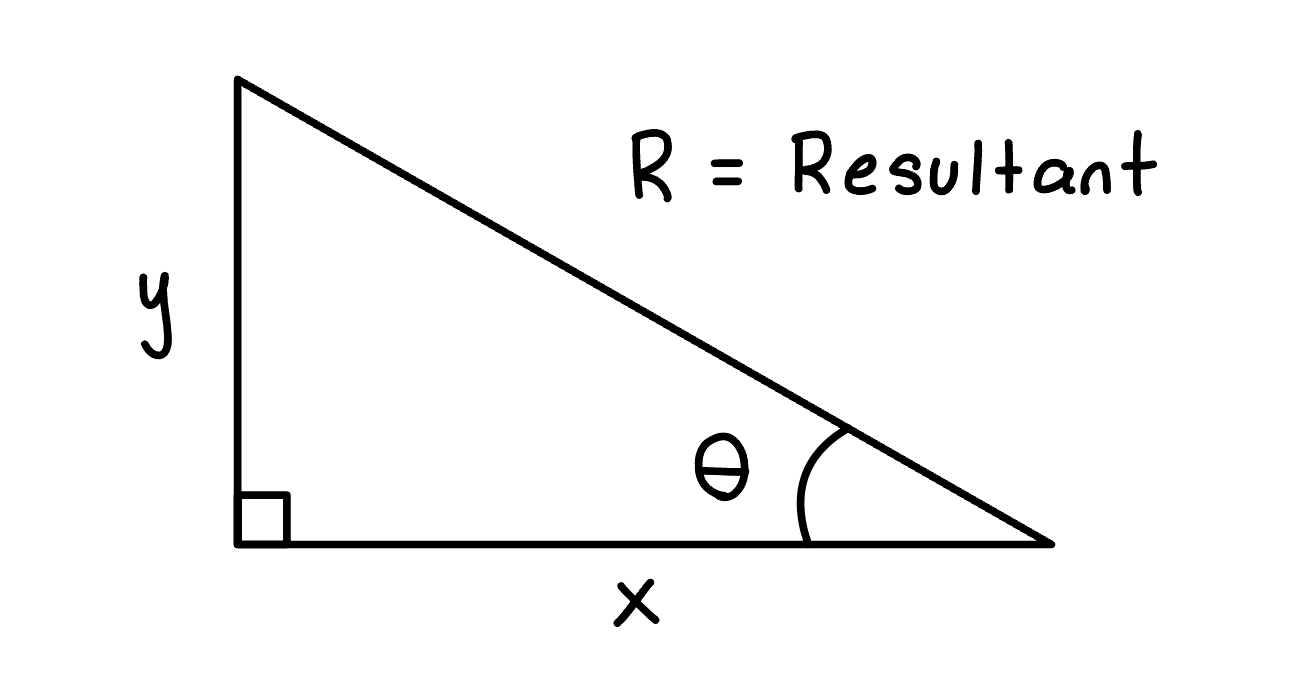
Trigonometry

Variables for Functions

h = hypothenuse

o = opposite

a = adjacent

sin = y-axis

cos = x-axis

R = Resultant

Functions

\sin \theta =\dfrac{o}{h}

\cos \theta =\dfrac{a}{h}

\tan \theta =\dfrac{o}{a}

Inverse Function

\theta =\sin ^{-1}\left( \dfrac{o}{h}\right)

\theta =\cos ^{-1}\left( \dfrac{a}{h}\right)

\theta =\tan ^{-1}\left( \dfrac{o}{a}\right)

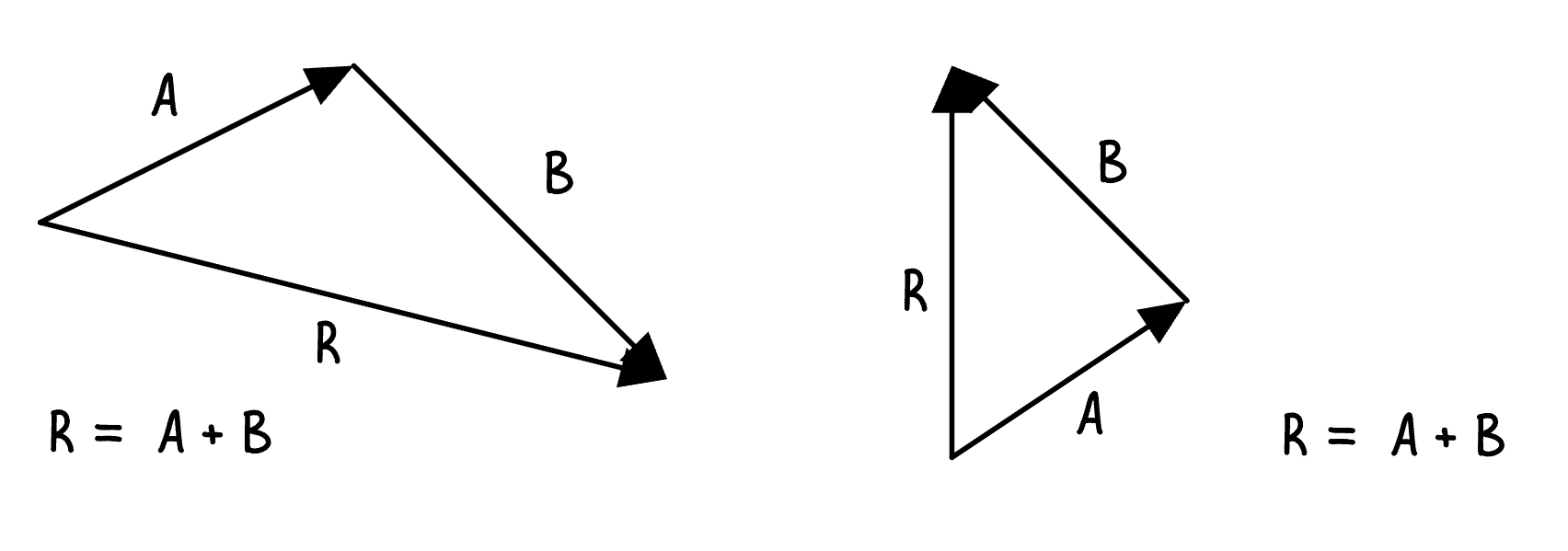
Pythagorean Theorem/Finding Resultant

h^{2}=o^{2}+a^{2}

R^{2}=A^{2}+B^{2}

Vocabulary

• Scalars - size or magnitude, described by single number

  • Temperature

  • Speed

  • Mass

  • Volume

  • Time

  • Density

  • Energy

  • Theta

• Vectors - has magnitude AND direction, represented by arrows

  • Velocity (speed with direction)

  • Displacement

  • Acceleration

  • Force

Chapter 2: One Dimensional Kinematics

Average speed - how fast something travels over a certain distance

• Average speed = Distance/Elapsed time

Change in: \Delta = finial - initial

Constant speed - constant velocity (constant magnitude and direction)

Average velocity - how fast an object's position changes over time

\overrightarrow{\overline{v}}=\dfrac{\Delta \overrightarrow{x}}{\Delta t}

Instantaneous velocity - velocity of an object at a specific moment in time, measures both the speed and direction of motion of the object at that precise instant.

\overrightarrow{v}=\lim _{\Delta t\rightarrow 0}\dfrac{\Delta \overrightarrow{x}}{\Delta t}

Average acceleration rate at which an object's velocity changes over a certain period of time.

\overrightarrow{\overline{a}}=\dfrac{\Delta \overrightarrow{v}}{\Delta t}

Displacement: \Delta \overrightarrow{x}=\overrightarrow{x}-\overrightarrow{x}_{0}

Slope: = rise/run = \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}

Speed vs. Velocity vs. Acceleration

1. Speed: How fast you're going, like on a speedometer. It's just a number, no direction.

2. Velocity: Speed with direction. It's how fast you're going and in which direction.

3. Acceleration: Changes in velocity. Speeding up, slowing down, or changing direction.

Velocity and Acceleration

• Velocity, no acceleration = constant velocity

• Velocity with acceleration = speeds up as it moves

• When acceleration and velocity have opposite directions, the object slows down and decelerates.

• Instantaneous velocity and instantaneous acceleration:

  • If inst. velocity goes from positive to negative, then acceleration must be negative.

Kinematic Variables

x = displacement

a = acceleration

v = velocity

v_{o} = initial velocity

t = time

Kinematic Equations

v=v_{o}+at

x=\dfrac{1}{2}\left( v_{o}+v\right) t

x=v_{o}t+\dfrac{1}{2}at^{2}

v^{2}=v_{o}^{2}+2ax

When solving these problems:

• Assume acceleration is constant

• Start motion at origin

• Start clock at time = 0

Freely Falling Bodies

• In absence in air resistance, all bodies fall vertically with the same acceleration.

• Acceleration always points down.

• Acceleration of freely falling body is call the acceleration due to gravity.

  • a = -g

  • a = -9.80 m/s²

  • g = 9.80 m/s²

    • Earth’s free-fall gravitational acceleration.

    • Scalar quantity

• At its maximum height, velocity = 0m/s

• Steps:

  • Draw picture.

  • Identify known/unknown variables.

  • Find needed kinematic equations.

  • Solve.

Free Fall Steps:

• Identify known quantities: initial velocity (if any), the acceleration due to gravity (usually -9.8 m/s²), and the time of motion (if given).

• Determine the unknown quantities

• Apply appropriate equation: x=v_{o}t+\dfrac{1}{2}gt

Chapter 3

r and x are the same

Displacement: \Delta \overrightarrow{r}=\overrightarrow{r}-\overrightarrow{r}_{o}

Average velocity: \overline{\overrightarrow{v}}=\dfrac{\Delta \overrightarrow{r}}{\Delta t}

Instantaneous velocity: \overrightarrow{v}=\lim _{\Delta t\rightarrow 0}\dfrac{\Delta \overrightarrow{r}}{\Delta t}

Instantaneous acceleration: \overrightarrow{a}=\lim _{\Delta t\rightarrow 0}\dfrac{\Delta \overrightarrow{v}}{\Delta t}

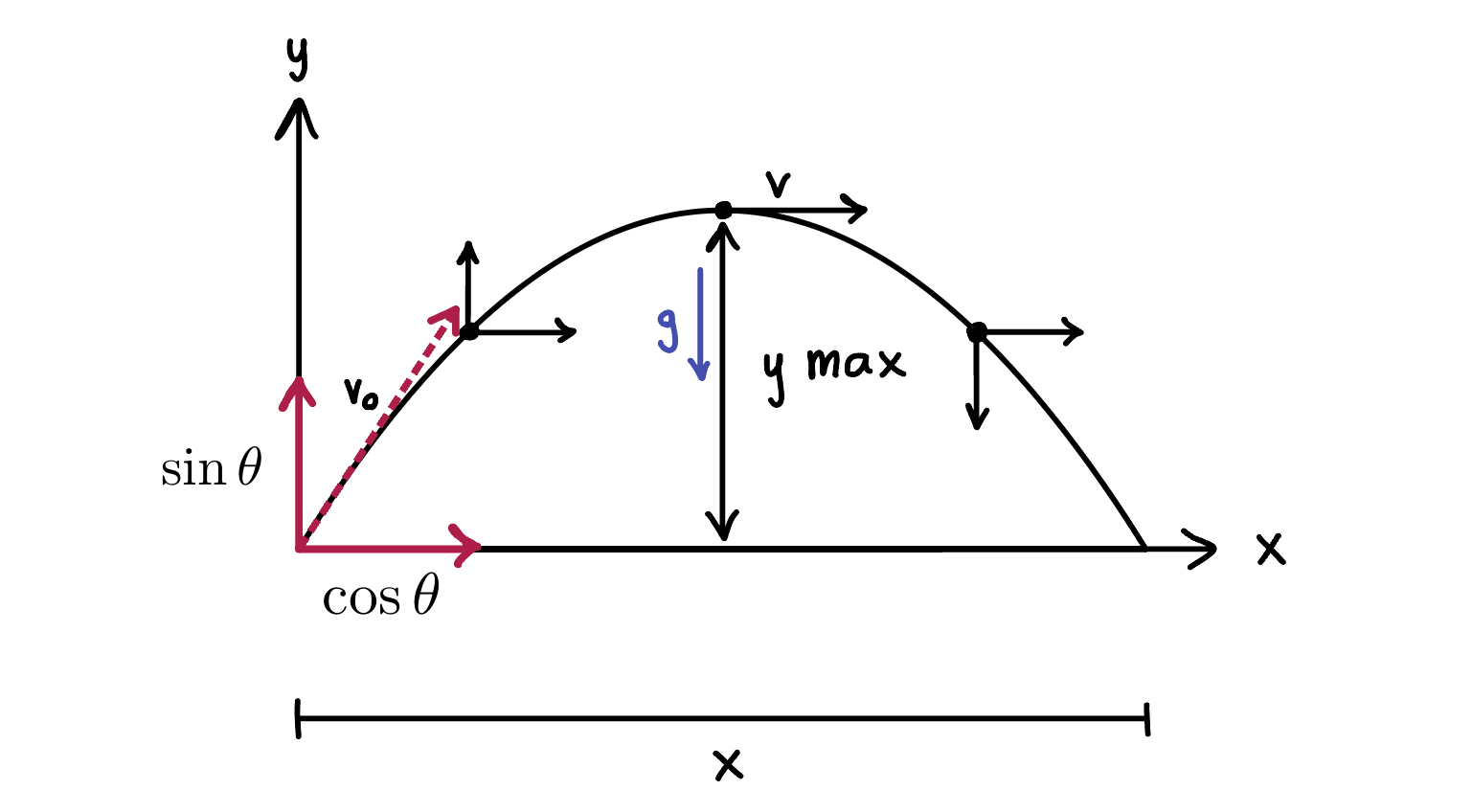
Projectile Motion

• Under the influence of gravity alone, an object near the surface of the Earth will accelerate downwards at 9.80 m/s²

• a_{y}=-9.80m/s^{2}

• a_{x}=0m/s^{2}

• v_{x}=v_{ox} = constant (same for both spaces)

• At the peak, v_{x}=0m/s

• Initial velocity:

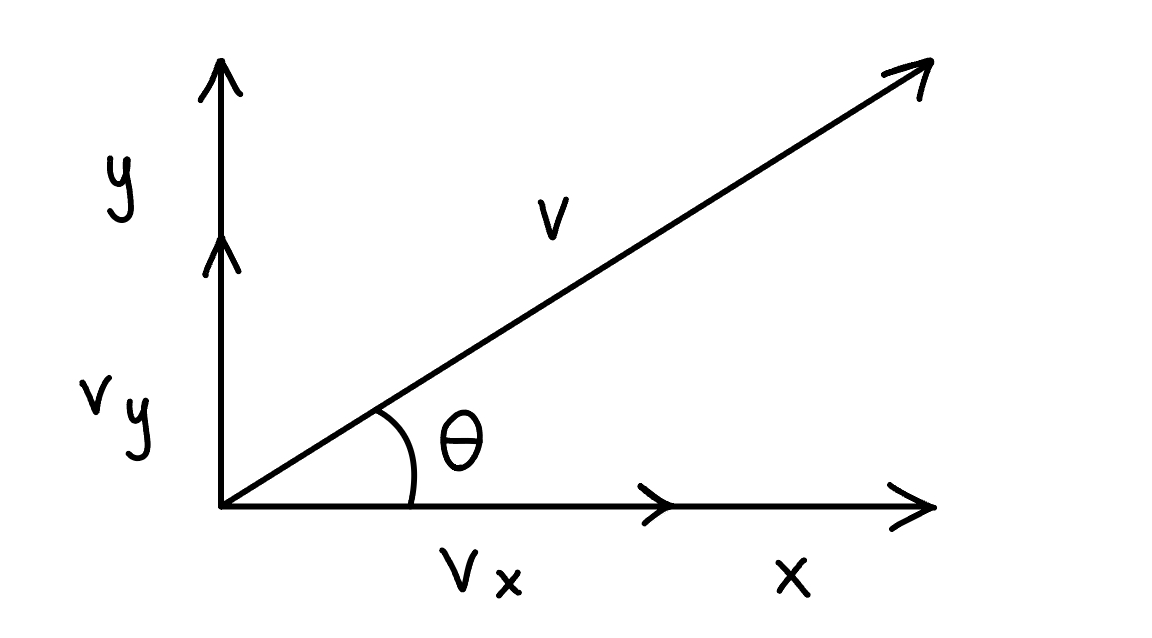
  • y-axis: \sin \theta =\dfrac{v_{oy}}{v_{o}}

  • x-axis: \cos \theta =\dfrac{v_{ox}}{v_{o}}

• Magnitude of velocity: v^{2}=v_{x}^{2}+v_{y}^{2}

• Angle for velocity vectors: \tan \theta =\dfrac{v_{y}}{v_{x}}

• Range:

  • R=v_{ox}t

  • OR

  • R=\left( v_{o}\cos \theta \right) t

• When creating x-component and y-component table for kinematic variables, remember to include directions = (+) or (-).

• Vector magnitude is always positive or zero.

• Maximum distance an object will go is at a 45 degree angle

• Steps:

  • Identify known/unknown variables.

  • Separate x and y components.

  • Find needed kinematics equations.

  • Find maximum height.

  • Determine range.

Relative Velocity

Relative velocity refers to the velocity of an object or observer in relation to another object or observer. It is the difference in velocities between two objects or observers as they move in different directions or at different speeds. Relative velocity takes into account the motion of both objects or observers and is often used to analyze the motion of objects in different frames of reference.

• The velocity of object A relative to object B is \overrightarrow{v}_{AB} , and the velocity of object B relative to object C is \overrightarrow{v}_{BC}

• The velocity of A relative to C is shown in the equation

  • \overrightarrow{v}_{AC}=\overrightarrow{v}_{AB}+\overrightarrow{v}_{BC}

• The velocity of object R relative to object S is always the negative of the velocity of object S relative to R \overrightarrow{v}_{RS}=-\overrightarrow{v}_{SR}

Kai’s AI response:

To solve a relative velocity problem, follow these steps:

1. Identify the objects involved: Determine the two objects or individuals whose velocities are being compared.

2. Define the frame of reference: Choose a reference point or frame of reference from which the velocities will be measured.

3. Determine the velocities: Find the velocities of the objects or individuals with respect to the chosen frame of reference. This may involve considering their initial velocities, accelerations, and any other relevant factors.

4. Determine the relative velocity: Calculate the relative velocity by subtracting the velocity of one object from the velocity of the other. Pay attention to the direction of motion.

5. Solve for the desired quantity: Depending on the problem, you may be asked to find the relative velocity, time of encounter, distance traveled, or any other related quantities. Use the given information and equations of motion to solve for the desired quantity.

6. Check your answer: Once you have obtained a solution, double-check your calculations and ensure that your answer makes sense in the context of the problem.

7. Remember to use appropriate units and consider any assumptions or simplifications made during the problem-solving process.

Extra

Average speed - how fast something travels over a certain distance: distance/elapsed time

Average velocity - how fast an object’s position changes over time: \overrightarrow{\overline{v}}=\dfrac{\Delta \overrightarrow{x}}{\Delta t}

Average acceleration - rate at which an object’s velocity changes over a period of time: \overrightarrow{\overline{a}}=\dfrac{\Delta \overrightarrow{v}}{\Delta t}

Speed vs. Velocity vs. Acceleration

1. Speed: How fast you're going, like on a speedometer. It's just a number, no direction.

2. Velocity: Speed with direction. It's how fast you're going and in which direction.

3. Acceleration: Changes in velocity. Speeding up, slowing down, or changing direction.

Velocity and Acceleration

• Velocity, no acceleration = constant velocity

• Velocity with acceleration = speeds up as it moves

• When acceleration and velocity have opposite directions, the object slows down and decelerates.