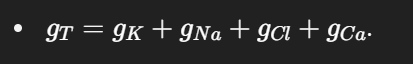Electrical properties of the membrane

The cell as a Donnan system

The Problem Setup

We have a semipermeable membrane separating two compartments:

• Side A: K⁺ and negatively charged proteins (Prot⁻, which cannot cross).

• Side B: K⁺ and Cl⁻.

At the start (initial state):

• Both sides have the same K⁺ concentration (0.1 M).

• Side A has Prot⁻ (0.1 M).

• Side B has Cl⁻ (0.1 M).

What Happens Over Time?

1. K⁺ and Cl⁻ can cross the membrane, but proteins (Prot⁻) cannot.

2. To reach equilibrium:

   • K⁺ distributes itself between sides A and B.

   • Cl⁻ redistributes too.

   • But Prot⁻ stays stuck on side A.

3. This causes an imbalance of charge across the membrane, → a small membrane potential.

Equilibrium State (shown in the right box):

• Side A:

  • [K⁺] = 0.133 M

  • [Cl⁻] = 0.033 M

  • [Prot⁻] = 0.1 M (fixed)

• Side B:

  • [K⁺] = 0.066 M

  • [Cl⁻] = 0.066 M

So, side A has more K⁺ and fewer Cl⁻, while side B has less K⁺ and more Cl⁻.

Rules of Gibbs–Donnan Equilibrium

• Electroneutrality:

  • On each side, total positive = total negative.

  • Example: On side A → [K⁺] = [Cl⁻] + [Prot⁻].

• Ionic product rule:

  • [K⁺]ₐ × [Cl⁻]ₐ = [K⁺]ᵦ × [Cl⁻]ᵦ.

• Electrochemical potential:

  • Must balance for permeant ions (K⁺, Cl⁻).

Key Consequence

• Because Prot⁻ is trapped on side A, more K⁺ stays there → side A becomes slightly negative compared to side B.

• This creates a Donnan potential (around –10 mV).

But:
👉 This potential is too small to explain the real resting membrane potential of excitable cells (–60 to –70 mV).
👉 That large negative potential comes mainly from the Na⁺/K⁺ pump + selective K⁺ permeability, not just the Donnan equilibrium.

✅ Simple Summary:
The Donnan effect happens when a non-permeant charged protein is trapped inside a cell. It causes unequal ion distribution (K⁺ and Cl⁻ shift), creating a small negative membrane potential (~ –10 mV). But this is not enough to explain the large negative resting potential of neurons and muscle.

Resting membrane potential

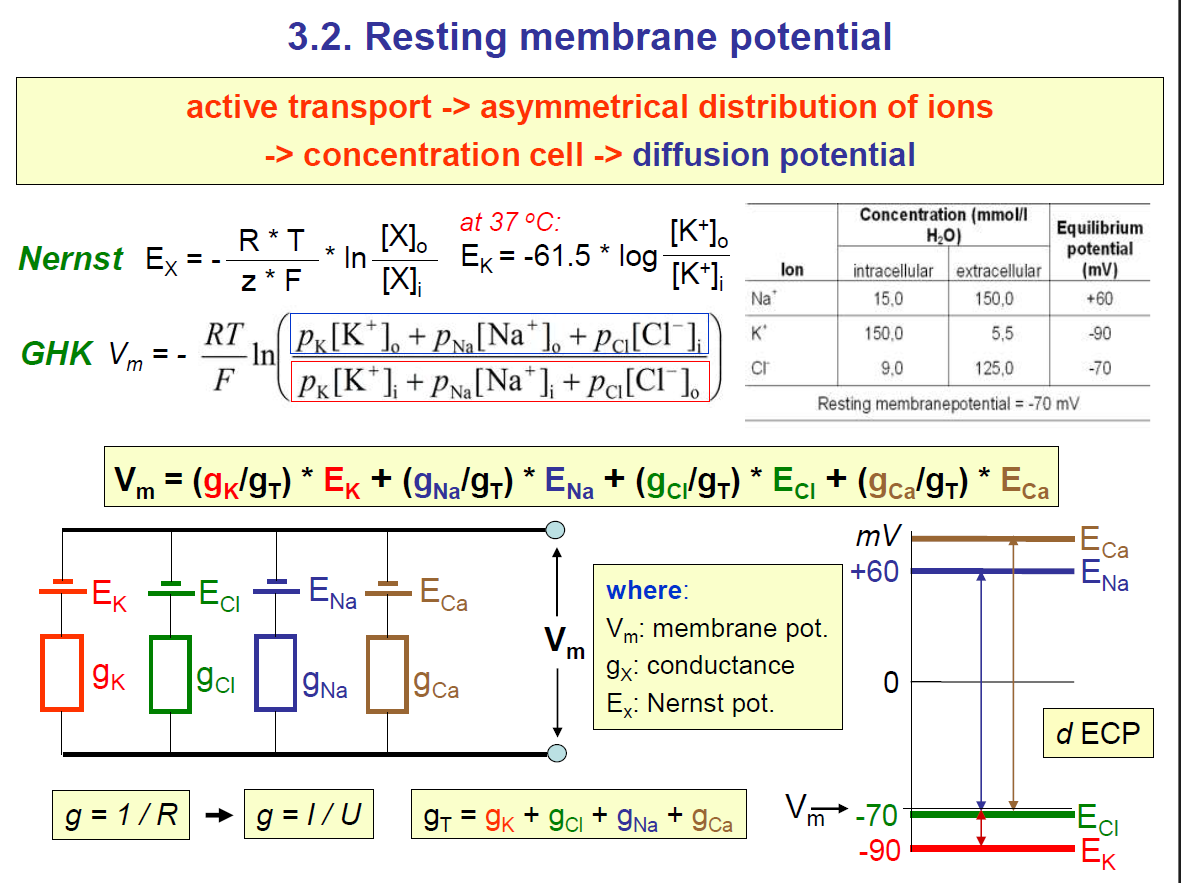
1. How the Resting Membrane Potential Forms

• Active transport (Na⁺/K⁺ pump):
  Pumps 3 Na⁺ out and 2 K⁺ in → creates an asymmetrical ion distribution.

• This means:

  • High [Na⁺] outside, low inside.

  • High [K⁺] inside, low outside.

  • Some Cl⁻ distribution too.

• Because of this, the cell behaves like a concentration cell → ions want to diffuse along their gradients, creating a diffusion potential.

2. Nernst Potential (Eₓ)

The Nernst equation tells you the equilibrium potential for a single ion (the voltage at which that ion’s net movement stops).

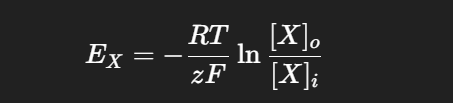
At body temperature (37 °C):

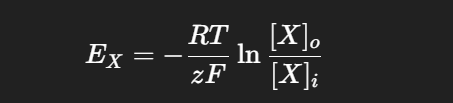
From the table in the slide:

• Na⁺: intracellular = 15, extracellular = 150 → E_Na ≈ +60 mV

• K⁺: intracellular = 150, extracellular = 5.5 → E_K ≈ –90 mV

• Cl⁻: intracellular = 9, extracellular = 125 → E_Cl ≈ –70 mV

🔑 3. Goldman–Hodgkin–Katz (GHK) Equation.

Cells are permeable to more than one ion, so the resting potential is not just E_K.

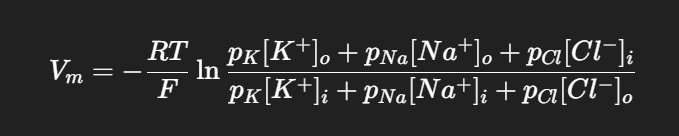
• Vm = membrane potential

• px = permeability of ion x.

• K⁺ usually dominates because the membrane is much more permeable to K⁺ than to Na⁺ or Cl⁻ at rest.

🔑 4. Equivalent Circuit Model

• The membrane is shown like an electrical circuit.

• Each ion has:

  • A battery (Eₓ) = its Nernst potential.

  • A resistor (gₓ) = its conductance (permeability).

• The actual membrane potential (V_m) is like the weighted average of all these “batteries,” weighted by conductance:

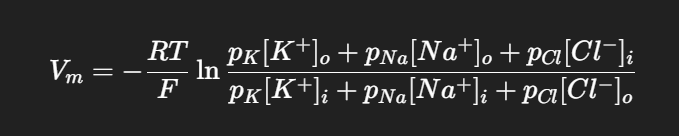
where

🔑 5. Putting It Together

• At rest:

  • K⁺ conductance is highest → Vm is close to E_K (–70 mV vs. –90 mV). Potassium has the highest conductance, so the membrane potential of the cell moves close to the equilibrium potential of potassium; thus, the membrane potential of the cell will be close to the equilibrium potential of potassium.

  • A little Na⁺ leaks in → Vm is not as negative as E_K. i.e the membrane potential is NOT EXACTLY at -90mv for potassium.

  • Cl⁻ usually balances passively around E_Cl (–70 mV).

• So the resting membrane potential is about –70 mV, sitting between E_K and E_Na, but much closer to E_K because of K⁺ permeability.

✅ Simple Analogy

Think of the cell like a room with many doors (ion channels):

• K⁺ doors are wide open → most of the “decision” about the voltage comes from K⁺.

• Na⁺ doors are mostly closed → Na⁺ has little influence.

• The pump keeps resetting the gradients like a janitor working in the background.

👉 In summary:

• The Na⁺/K⁺ pump creates the gradients.

• The Nernst equation gives each ion’s “preferred voltage.”

• The GHK equation + circuit model explains the actual Vm as a weighted average.

• At rest, Vm ≈ –70 mV, closer to E_K than E_Na.

EXAM TIP:

Changing the concentration of the ions, such as Na+ and Cl-, does not really affect the membrane potential of the cell.

But changing the concentration of potassium would affect the membrane potential of the cell since the conductance of potassium is the highest at rest.

Because changing the concentration of potassium, the equilibrium potential of potassium also changes, so this would change the membrane potential

Consequences of changes in ion conductances

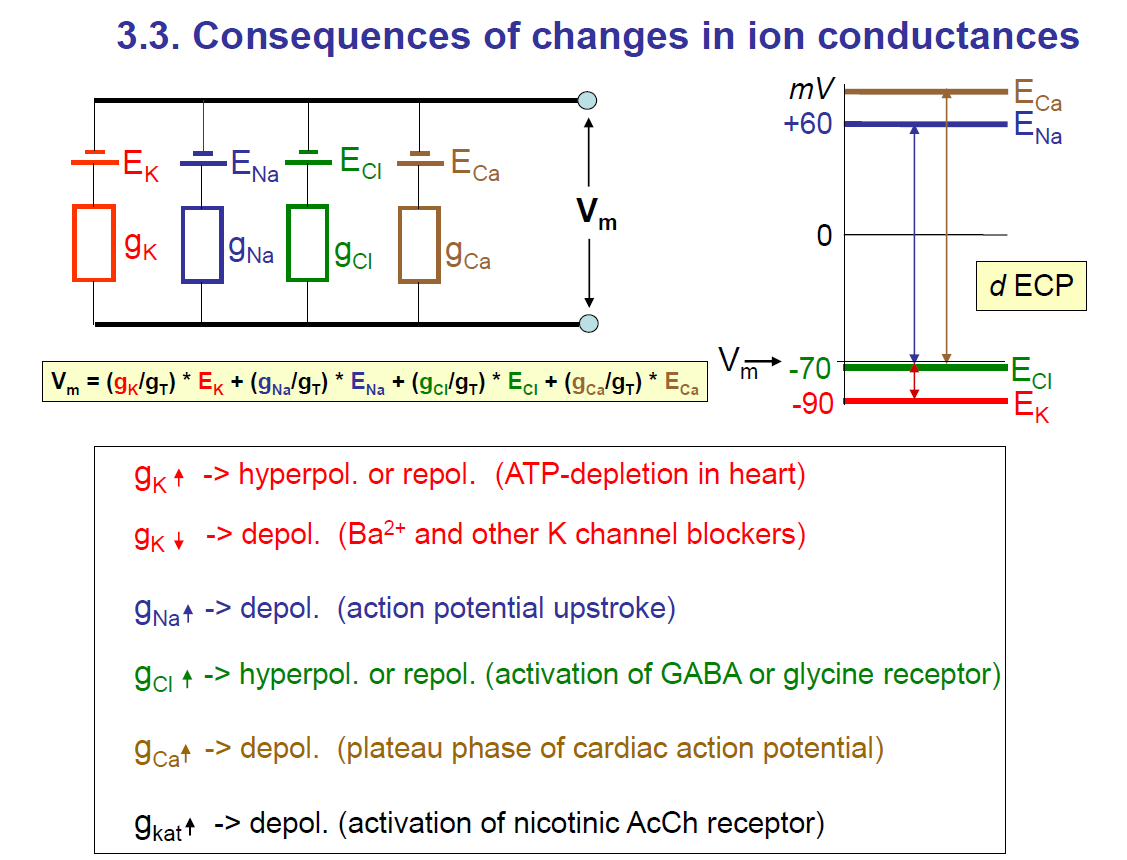
1. The basic idea

• The membrane potential VmV_m is a weighted average of the equilibrium potentials (E_K,E_Na,E_Cl,E_Ca) of different ions.

• The weight is determined by how conductive (open/permeable) the membrane is to each ion.

The formula shown:

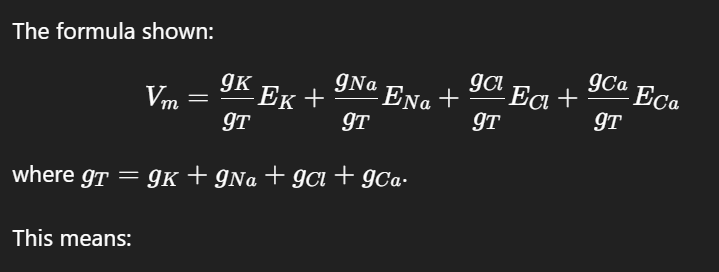
This means:

• If potassium conductance (g_K) dominates, → V_m is close to EK≈−90 mV.

• If sodium conductance (g_Na) dominates, → V_m moves toward ENa≈+60 mV.

• If calcium conductance (g_Ca) dominates, → Vm moves toward ECa≈+120 mV.

• If chloride conductance (g_Cl) dominates, → VmV_m moves toward ECl≈−70 mV.

Key note: The membrane potential moves towards the equilibrium potential of the ion with the highest conductance.

2. Effects of increasing or decreasing conductances

• gK↑g_K \uparrow (more K⁺ leaving)
  → Hyperpolarisation (more negative, toward –90 mV) or repolarisation.
  Example: ATP depletion in the heart activates K⁺ channels.

• gK↓ (less K⁺ leaving)
  → Depolarisation (membrane becomes less negative).
  Example: Ba²⁺ or K⁺ channel blockers.

• gNa↑ (more Na⁺ entering)
  → Depolarisation (toward +60 mV).
  Example: action potential upstroke.

• gCl↑(more Cl⁻ moving)
  → Hyperpolarisation or repolarisation (toward –70 mV).
  Example: activation of inhibitory GABA_A or glycine receptors.

• gCa↑(Ca²⁺ entering)
  → Depolarisation (toward +120 mV).
  Example: plateau phase of cardiac action potential.

• gkat↑ (non-specific cation conductance, e.g. nicotinic ACh receptor): since the receptor is non-specific, the cations can pass through
  → Depolarisation (because Na⁺ and K⁺ flow through, the net effect is depolarising).

3. Graph on the right

• Shows the driving forces for each ion:

  • EK≈−90 mV (red line, very negative)

  • ECl≈−70 mV (green line, near resting potential)

  • ENa≈+60 mV (blue line, strongly positive)

  • ECa≈+120 mV (brown line, very positive)

• Resting potential is usually near –70 mV, closer to E_K, because K⁺ conductance dominates at rest.

✅ Key takeaway:
The membrane potential is a balance between different ionic conductances. By opening or blocking channels, cells can hyperpolarise, depolarise, or repolarise. This is the basis of excitability in neurons, the heart, and muscle.

Resting membrane potential

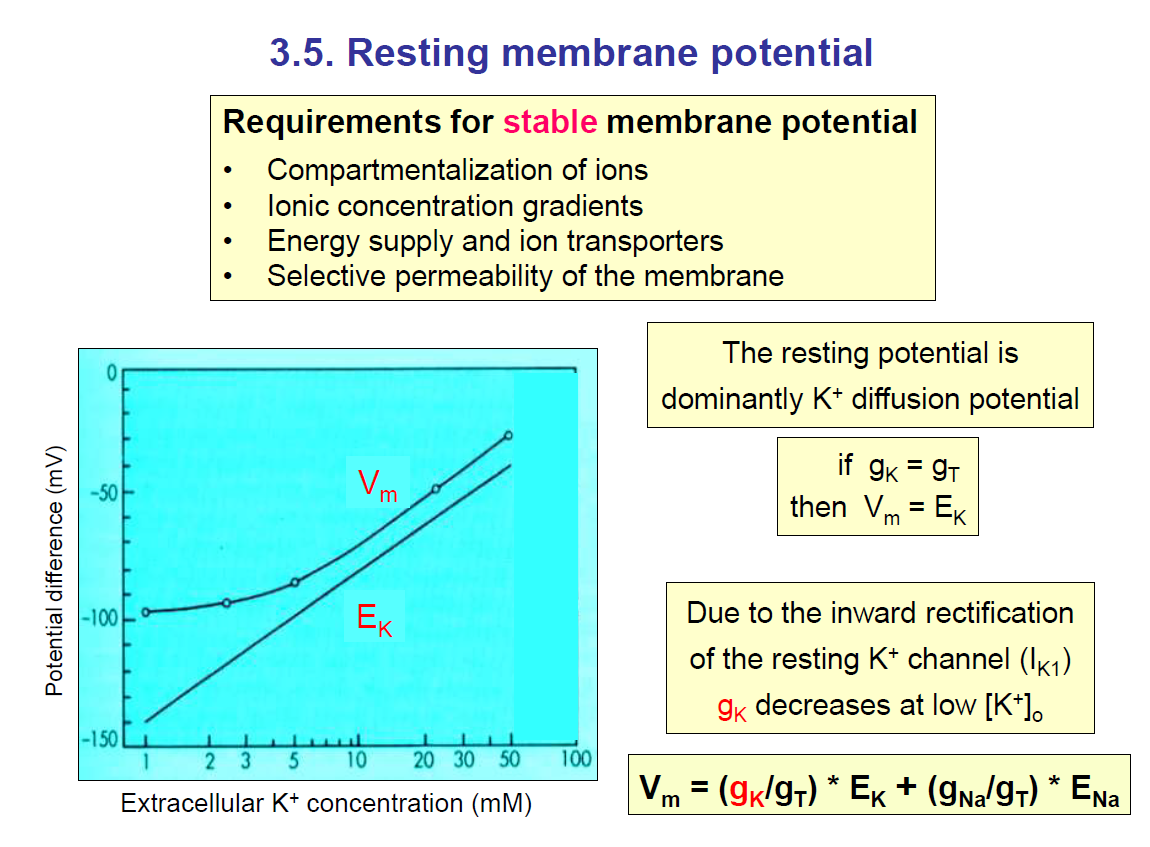
• From the diagram on the left, you can see that increasing the extracellular concentration of potassium would increase the equilibrium potential of potassium.

• Also, you can see how the membrane potential (Vm) also changes (increases). This is because the conductance of K+ is really high.

Contribution of the Na+/K+ pump to the resting membrane potential

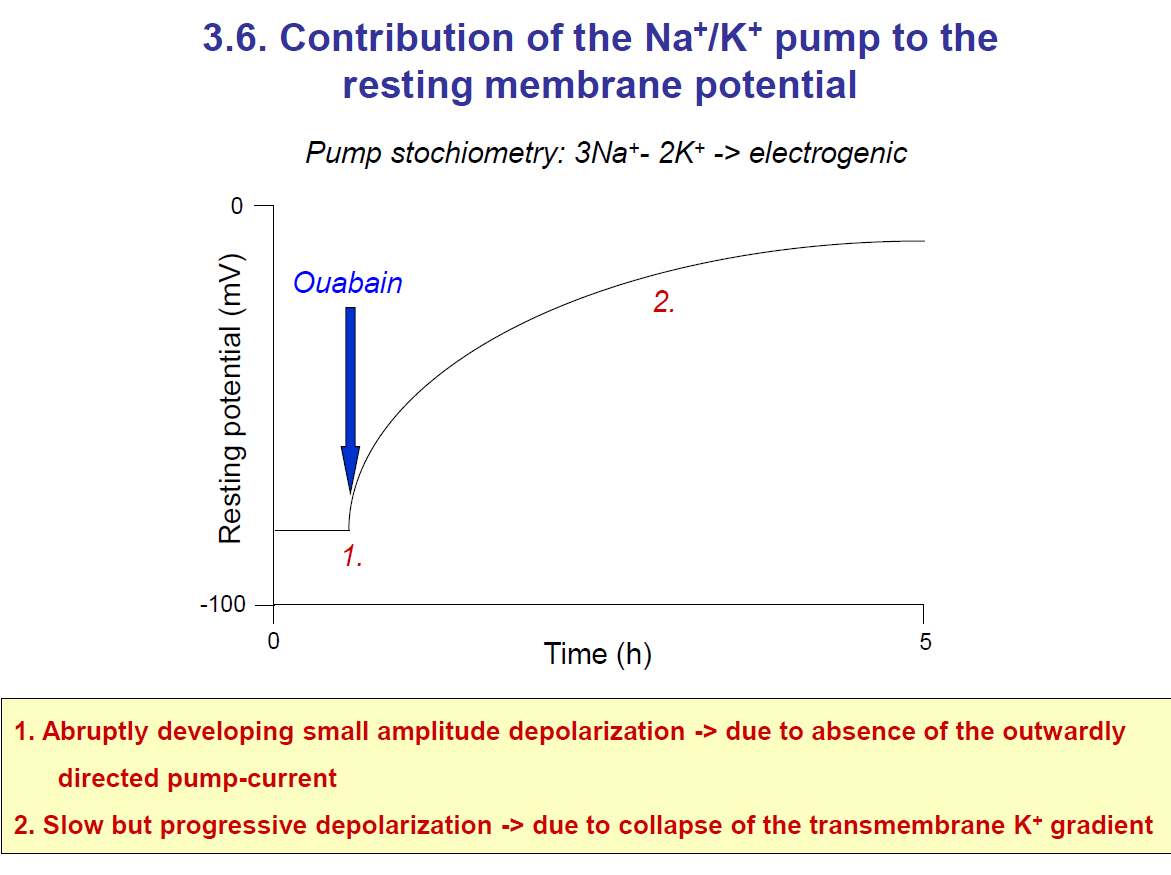
Key Note:

• Ouabain blocks the Na⁺/K⁺ pump (3 Na⁺ out / 2 K⁺ in).

• Immediate effect: loss of the pump’s electrogenic outward current → small, abrupt depolarisation.

• Long-term effect: Na⁺ starts accumulating inside the cell, and K⁺ starts decreasing inside (since leak channels keep working, but the pump can’t restore gradients).

• This causes the K⁺ gradient to collapse, shifting the membrane potential away from Ek​ (–90 mV) toward 0 mV → slow progressive depolarisation.

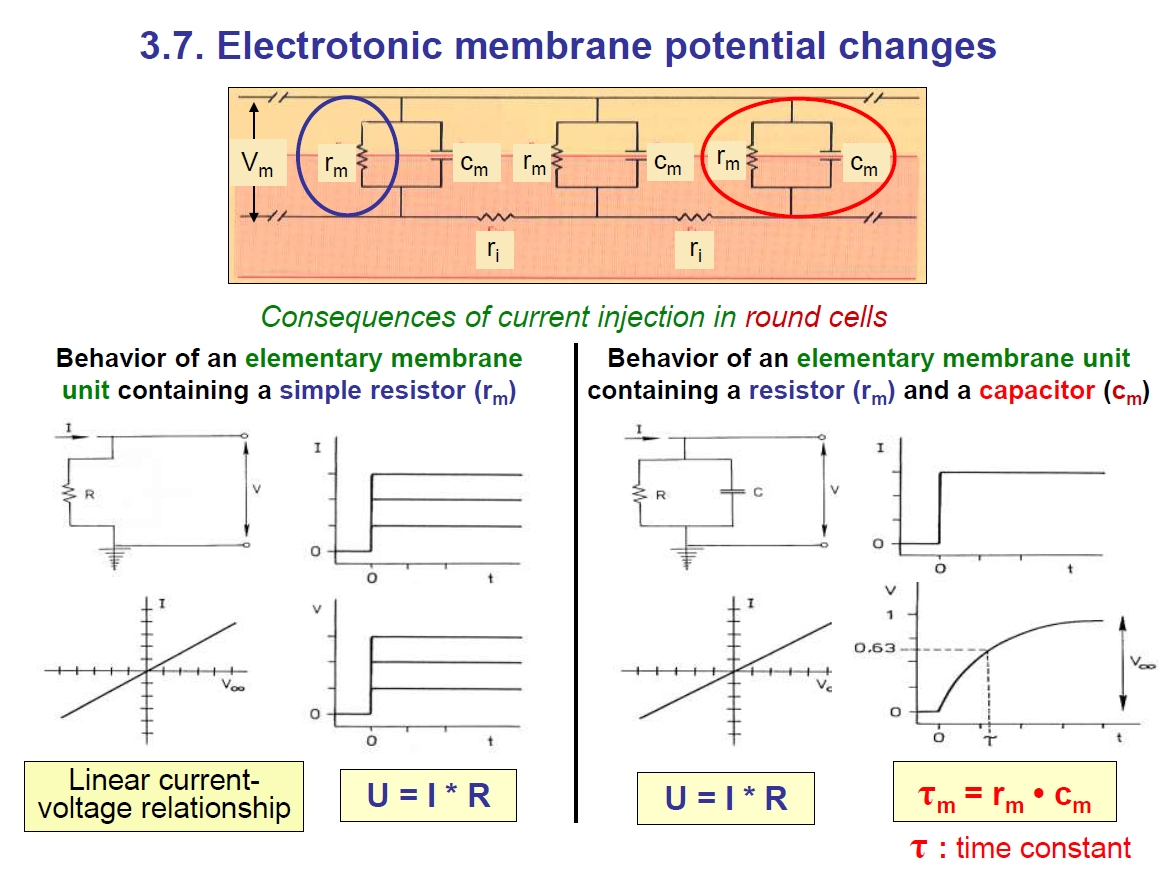
1. Membrane as an electrical circuit

Cells behave like electrical circuits.

• The lipid bilayer acts like a capacitor (Cm) → it stores charge.

• The ion channels act like a resistor (Rm) → they let current leak through.

• The cytoplasm/extracellular fluid acts like a conductor.

So, the cell membrane = resistor (Rm) in parallel with a capacitor (Cm).

Take note: the faster the conduction, the lower the time constant.

• When there is resistance, some energy is lost

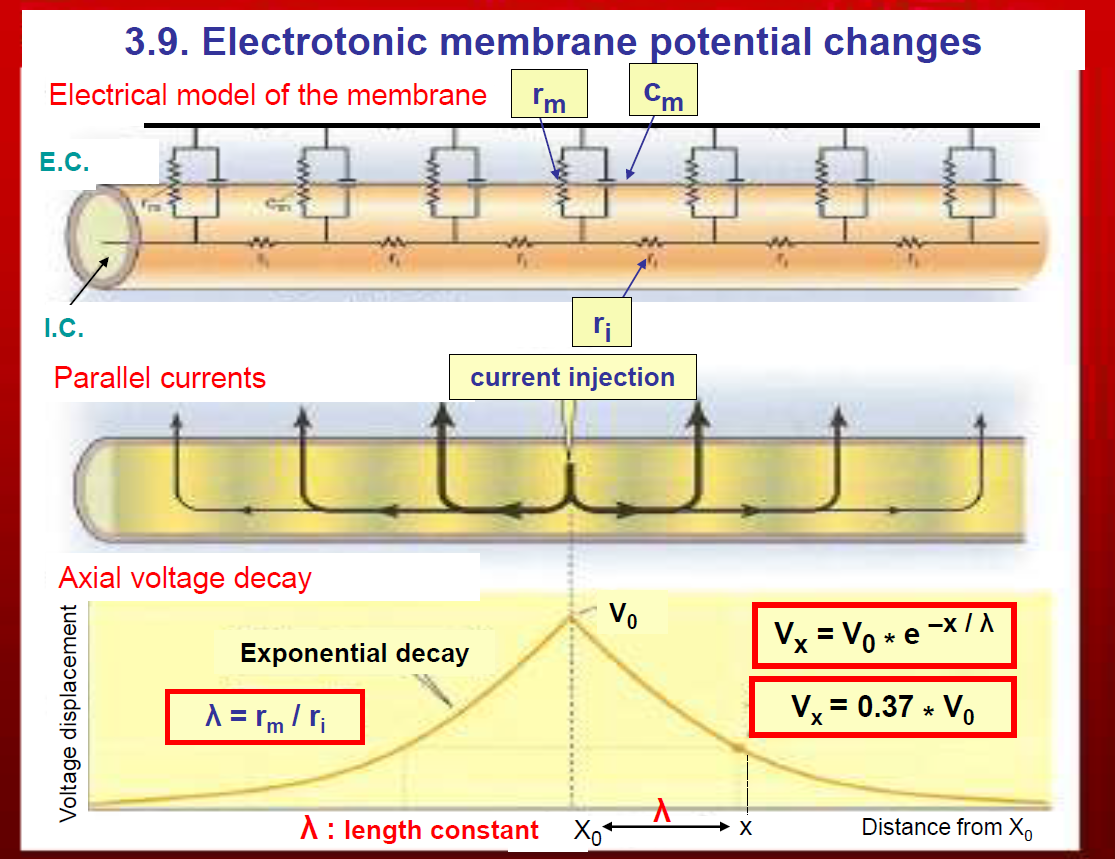
(3.9. Electrotonic membrane potential changes)

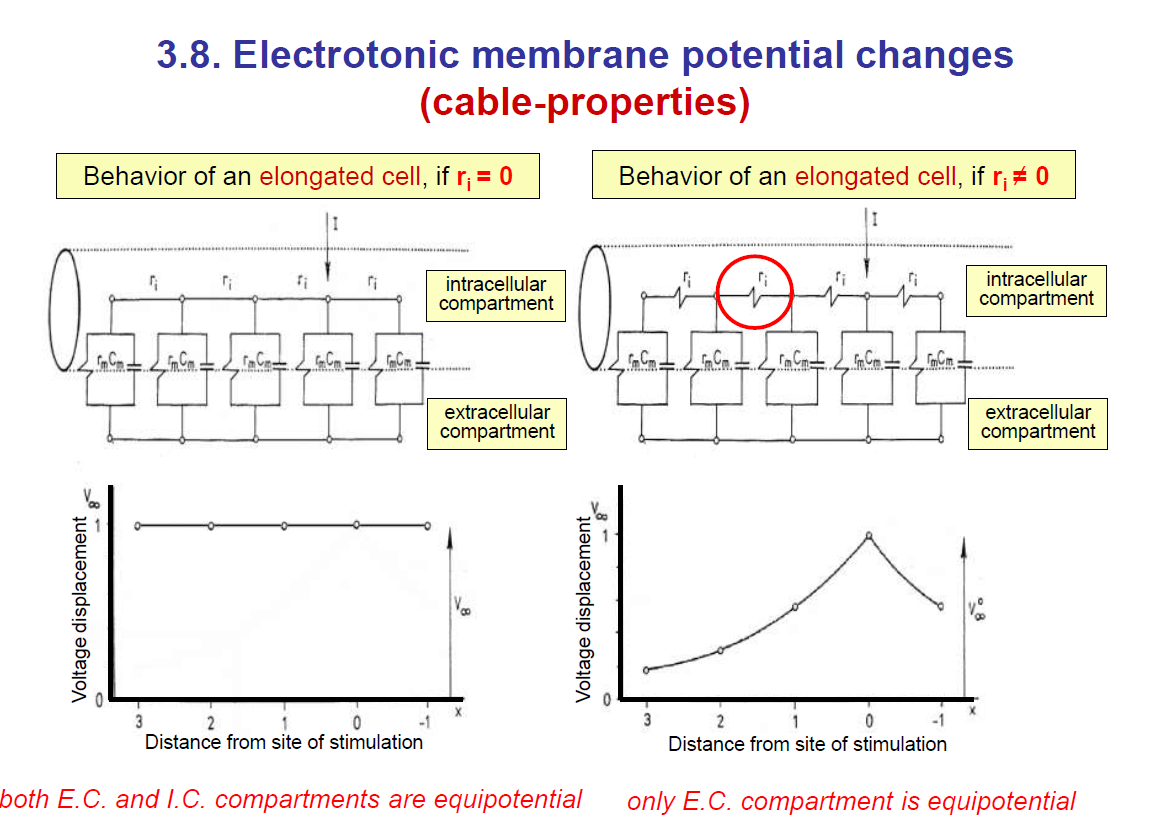
This shows how current spreads passively along a neuron’s membrane.

1. Electrical model of the membrane

• The membrane is modelled as:

  • Resistor (rm) → represents membrane resistance (ion channels).

  • Capacitor (cm) → represents the ability of the lipid bilayer to store charge.

  • Axial resistance (ri) → resistance of the cytoplasm inside the neuron.

This creates a network of resistors and capacitors along the axon or dendrite.

2. Current injection and parallel currents

• If you inject current at one spot, some flows along the inside of the neuron (axially) and some leaks outward across the membrane.

• Because of this leakage, the voltage decreases as you move further away from the injection site.

3. Axial voltage decay

• The voltage falls off exponentially with distance:

  • 

r_m = membrane resistance

r_i = intracellular resistance (i.e. resistance of the cytoplasm inside the neuron).

T_m = membrane time constant

T_i = time constant for current flow inside the axon.

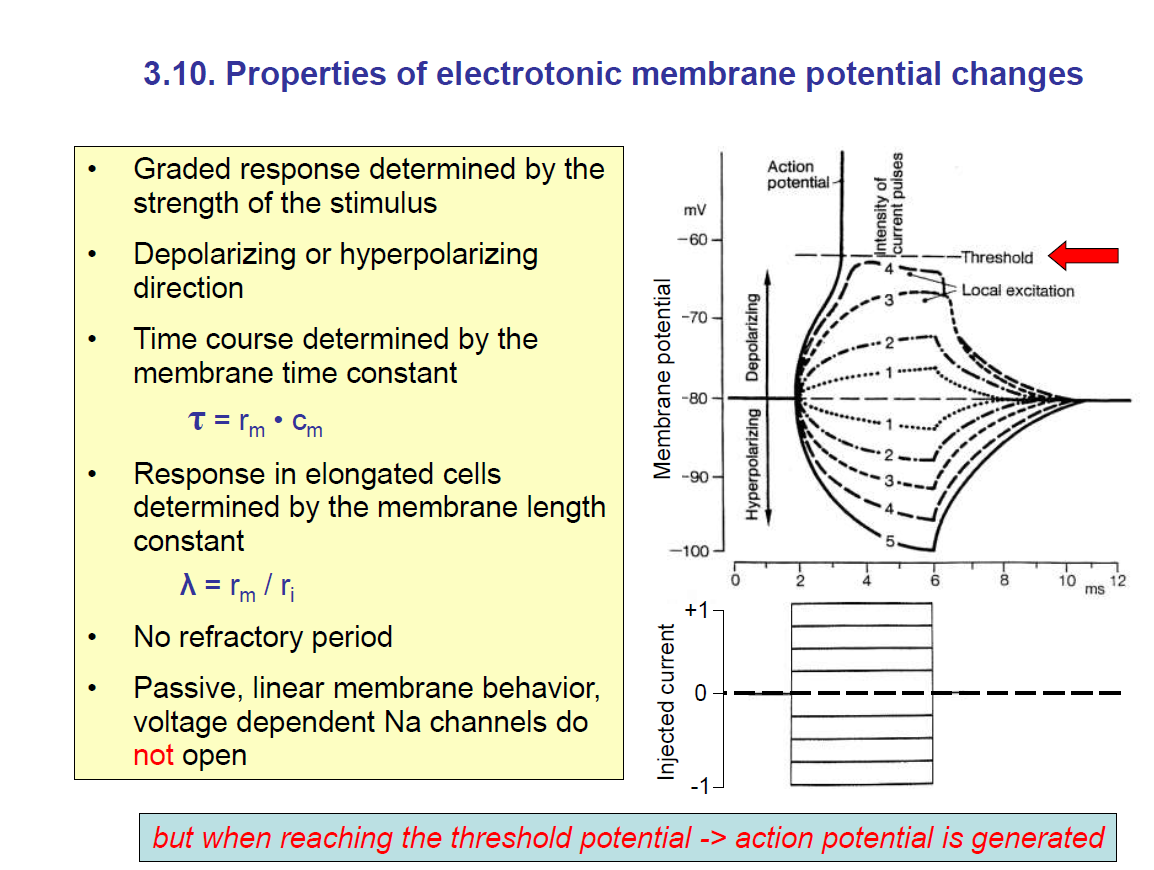
(3.10. Properties of electrotonic membrane potential changes)

This slide explains the functional properties of passive responses.

1. Graded response

• The change in membrane potential depends on the strength of the stimulus (more current → bigger depolarisation or hyperpolarisation).

• Unlike an action potential, it is not all-or-nothing.

2. Depolarising or hyperpolarising

• Injecting positive current → depolarisation.

• Injecting negative current → hyperpolarisation.

3. Time constant (τ)

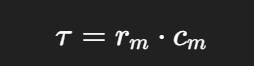
• Determines how fast the membrane potential changes.

• Larger r_m or C_m → slower response. Thus, a longer time constant.

• Recall: r_m = membrane resistance; C_m = membrane capacitance.

4. Length constant (λ\lambda)

• The length constant determines how far a signal spreads before decaying.

5. Other properties

• No refractory period (unlike action potentials).

• Passive and linear behaviour (no active Na⁺ channel involvement).

• If depolarisation reaches threshold, then voltage-gated Na⁺ channels open → action potential generated (nonlinear switch to active signalling).

Graph (on the right)

• Shows graded potentials:

  • Small currents → small voltage changes.

  • Larger currents → larger changes.

  • At a critical depolarisation (threshold), instead of a graded response, the cell fires an action potential (sharp upward spike).

✅ Summary in plain words:
Electrotonic potentials are passive, graded, and decay with time and distance. They depend on two key constants:

• τ\tau (time constant) → how fast the voltage changes.

• λ\lambda (length constant) → how far the voltage spreads.
  They don’t have refractory periods and can summate, but if they reach threshold, they trigger an action potential.

• Graded response determined by the strength of the stimulus: The stronger the stimulus, the higher the change in the membrane potential.

• The stimuli can cause hyperpolarisation or depolarisation.

• Time course is determined by the time constant:

  t = rm x cm

• NOTE: A passive membrane is one without a Na+ ion voltage-gated channel.

• When the electrotonic membrane potential reaches the threshold potential, an action potential is generated.