Unit 1-5 Ap Stats Test.
Unit 1: One Variable Data
Vocabulary
Categorical Data: Grouped into different categories (E.g., colors, qualities).
Quantitative Data: Grouped by numerical value (E.g., age, quantities).
Frequency Table: Number of individuals of each value.
Relative Frequency Table: The proportion/percentage of individuals having each value.
Parameter is numerical value describing population
Statistic is numerical value describing a sample
Describing Associations
Make a claim (is or isn’t).
Support claim (compare percentages).
Include context (variables).
Marginal Distributions summarize the frequency of a single variable (Pass/Total)
Conditional Distributions summarize one variable given another variable (Pass/Didn’t Study).
Measures of Center
Mean
Formula is sum/total frequency
Sensitive to extreme outliers
High outlier = higher inflates
Low outlier = lower deflates
Follows the skew
Median
Middle value
Not affected by outliers
Modes
Unimodal: One peak
Bimodal: Two peaks
Mean in histogram
x=15(0)+11(1)+15(2)…/75 = value
Measure of Spread
Range: max-min
IQR: Q3-Q1
Outliers:
Q3+(1.5×IQR)
Q1-(1.5×IQR)
Standard Deviation: Calculator
High variability is low sd
Low variability is high sd
Describing Distributions (CSOS)
Context: Relevant background info
Shape: Symmetric, skewed, unimodal, or bimodal
Center: Mean/median
Spread: Range, IQR, or standard deviation
Percentiles
Cumulative Relative Frequency: Percentiles Graphed
Z Score: Number of standard deviations above/below mean
(Data point - mean)/standard deviation
Normal Curve
It is a symmetric and “bell shaped”
The mean = median at the center
68-95-99.7 rule
When in between standard deviations:
Find z-score
Use table A
Adding/Subtracting each data value:
Mean increases/decreases by same
Median increases/decreases by same
Range has no change
IQR has no change
SD has no change
Shape has no change
Multiplying each data value:
Mean is multiplied/divided by amount
Median is multiplied/divided by amount
IQR: Multiplied and divided by constant
SD: Multiplied/divided by constant
Shape: No change
Unit 2: Two Variable Data
Vocabulary
Bivariate Data is two variables → visualized in scatterplots
Explanatory (independent) is the x-axis, it explains response
Response (dependent) is the y-axis, it responds to the trends
Least Squared Regression Line (LSRL).
Minimizes the sum of squared residuals between the data and model
Residuals are distances in the response too each data point
Residual = Actual - predicted point
Leverages
Low leverage is closer to x
High leverage are closer to y (affects LSRL)
Influential Points If removed, changes the slope
Correlation Coefficient: Means data is close to LSRL
Number between -1 to 1
Slope and Y-intercept (y=a+bx)
Slope refers to rate of change
Y intercept is predicted value when independent variable is zero
Describing Scatterplots (CDOFS)
Context
Direction (postitive/negative)
Outliers
Form (linear/not linear)
Strength (strong, moderate, weak).
Residual Plot: Focused on residuals, centered at zero, random is good
Regression Tables:
r² is the coefficient which explains the percentage of variance is explained
square root r^ to get r (correlation coefficient)
Standard Deviation (s)
is a measure of the amount of variation of the values of a variable about its mean
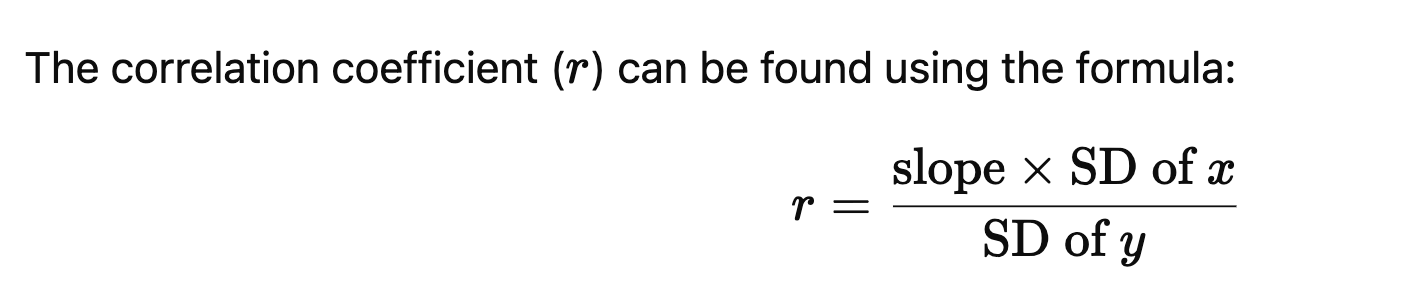
Unit 3: Collecting Data
Vocabulary
Census is collecting of whole population
Sample is a subset of individuals
Generalization occurs when studying a large population
Statistical significance is that when something is so unlikely to happen it was not by random change
Types of Bias
Sampling bias is when some people are more likely to be selected
Leads to undercoverage (others have a reduced change).
Types of Samples
Stratified random sample divides in homogenous groups and selects a few
Systematic sample selects in fixed intervals
Voluntary response sample individuals choose to participate
Simple random sample (SRS) using random number generator to get samples
Cluster Sample: Dividing in clusters and selecting aroound thoose
Using SRS
Define population
Determine sample
Assign numerical values
Use RNG
Correspond numerical value
Selection Bias:
Non response is those who do not respond
Under-coverage is others are not apart of sample
Voluntary Response is when others usually have stronger opinions
Survey bias
Confusing wording sways or misleading
Self reported bias inaccurately report their own traits
Experiments:
Randomly assigned experimental units
Those assigned have an explanatory variable (purposely manipulated).
Treatments are the different levels or conditions
Response variable is the measured outcome
Confounding variable can influence the response variable
Compare, random assignment, replication, and control
Completely Randomized Design are when units are assigned at complete random
This reduces the confounding
Variation are natural fluctuations that occur
Randomized Complete Block Design are when experimental units are blocked by similar traits
Matched pairs are paired by similar traits and one is assigned treatment and other is control
Control is often placebo too
Unit 4: Probability
Ideas of Probability
Empirical probability is determined by physically performing many trials.
Simulated probability uses technology to mimic a random process.
Probability formula (for equally likely outcomes):
P(A)=Number of outcomes in A/Total possible outcomes
A small number of repetitions can lead to unreliable results due to sampling variability.
Formulas
Intersection (A ∩ B): Outcomes common to both events (INTERSECTION/ADD)
Union (A ∪ B): Outcomes in A, B, or both (UNION/OR)Mutually Inclusive Events (Disjoint).
Mutually Inclusive: Two events can happen together
FORMULA: The probability of mutually inclusive events is calculated using the addition principle: P(A ∪ B)=P(A)+P(B)-P(A∩B).
VENN DIAGRAM: Has an overlapping middle
Mutually Exclusive Events: Events that cannot occur at the same time
FORMULA: P(A ∪ B) = P(A) + P(B)
HOW TO CHECK: P(A ∩ B) = 0
VENN DIAGRAM: Has NO overlapping middle
Independent vs. Not Independent Events
Independent Events: The occurrence of one event does not affect the probability of the other.
Independent event multiplication rule: P(A ∩ B) = P(A)xP(B)
To determine is to solve whenever P(A∩B) = P(A) P(B)
P(A)=P(A|B)
Conditional Probability: Describes the probability that one event happens given that another event is already known to have happened.
FORMULA: P(A|B)=P(A∩B)/P(B)=P
(both events occur)/P(given event occurs)
Expected Values: Its average value over many, many trials of the same random process E(x).
The mean/expected value, is the long-run average value of the variable after many, many trials of the random process. It is denoted by 𝜇x or 𝐸 (𝑋).
Standard deviation is measure of spread, it indicates how far, on average, data points deviate from the mean, with a larger standard deviation signifying a wider spread in the data.
Multiplying random variable by a constant
Mean: multiples/divides by that constant
Standard deviation: does not change
Variance: multiples/divides by that constant squared
Shape: remains the sameAdding random variable by a constant
Adding by constant
Mean: multiples/divides by that constant
Standard Deviation: Multiplied by the absolute value of the constant
Variance: The variance is scaled by the square of the constant "c".
Shape: remains the same
BINS:
Binary
Independent
Number of trials is fixed
Same probability
Binomial: The likelihood of getting a specific number of "successes" in a fixed number
ux=np
ox= sqr[(np(1-p)]
Geometrics: The same probability of success for each trial
ux=1/p
ox=(sqrt1-p)/p
CDF:Calculates the probability that a random variable will be less than or equal to a specific value within a given distribution
E.g., getting at most 3 heads in 5 coin flips using a binomial distribution, you would use the "binomcdf"
PDF: the probability of a continuous random variable taking on a specific value within a given range
Taking on a specific value within a given range
Unit 5: Samplings
Sampling Distributions
The distribution of a statistic from all possible samples of a given size n from a population.
Population: Whole population
Parameter describes some characteristics of a population
Sample: Sample from population (s)
Statistic that describes characteristics of a sample
Unbiased Estimator: The mean of the sampling distribution is equal to the population parameter.
Reducing Variability: Increasing sample size reduces the spread of the sampling distribution.
Sampling Distribution of Sample Proportions (p̂)
NORMALITY: Large counts conditional: Successes and failures must be greater or equal to 10 np≥10 n(1-p)≥10
INDEPENDENCE FOR MEAN: The sample size (n) must be less than 10% of the population size (N) n<.1N
UNBIASED FOR SD: Large counts condition: np≥10 and n(1−p)≥10
Means (x-)
NORMALITY: Central Limit Theorem (𝑛 ≥ 30 ensures normality)
INDEPENDENCE FOR MEAN: Random sample (unbiased)
10% SD RULE: Large counts condition: Np≥10 and n(1−p)≥10
Unit 6: Sample proportions
Significance Testing:
Tests for statistical significance tell us what the probability is that the relationship we think we have found is due only to random chance
Reject or fail to reject null hypothesis
Confidence Interpretations
Confidence Interval: "We are __% confident that the true [parameter] is between bound] and [bound]."
YES: "We are 95% confident that the true proportion of students who pass the AP Statistics exam is between 72% and 85%."
FOR TWO PROPORTION: Needs separate p hat’s to find standard error.
Confidence Level:
If we were to repeat this process many times, about __% of the confidence intervals we create would contain the true [parameter]
YES: If we were to take many random samples of the same size, about 95% of the resulting confidence intervals would contain the true mean height of all students at our school.
FOR TWO PROPORTION: Uses phat combined for like y1 and y.