Final - Chapters
Chapter 9: Design of Experiments and Analysis of Variance
9.1 - Elements of a Designed Experiment
The response is the variable of interest in the experiment. This is also refered to as the dependent variable.
True or false? The response variable is quanitative in nature?
Factors are the variables that effect the response/dependent variable.
Quanitative factors are measured numerically
Qualitative factors are measured are not on a naturally occuring numerical scale
Factors are the independent variable
Factor levels are the values of the factor used in the experiment
The treatments of an experiment are the factor-level combinations used.
Ex: the effect of the factor Gender on GMAT scores, then the treatments of the experiment are the two levels of gender - male and female
An experimental unit is the object on which the response and factors are observed or measured
A designed experiment is one where the analyst controls the treatments and the method of assigning the experimental units to each treatment
An observational study is one which the analyst simply observes the treatments and the response
What is the objective of desiging a study?
Maximize the amount of information obtained about the relationship between the treatments and the response
9.2 - The Completely Randomized Design: Single Factor
Completely randomized deisgn - a design in which the experimental units are randomly assigned to the k treatments or in which independent random samples of experimental units are selected for each treatment
What is a balanced design?
When an equal number of experimental units are assigned to each treatment
Ho = u1 = u2 = uk
Ha = at least two of the k treatment means differ
How is the variation between the treament means calculated?
Sum of Squares for Treatment (SST) - sum(treatment mean - overall mean)².
How is the sampling variability within the treatments calculated?
Sum of Squares for Error (SSE) - sum(response measurement - corresponding treatment mean)²
What is the Mean Square for Treatments?
MST = SST/(k-1)
What is the Mean Square for Error?
MSE = SST/(n-k)
F= MST/MSE
What must be assumed?
random sampling
normal distribution
9.3 - Multiple Comparisons of Means
How do we know which means are different?
we use the pairwise comparisons of treament means
c = k(k-1)/2
In this case, alpha is called the experimentwise error rate
Type I for comparison = comparisonwise eroor rate (CER)
Guidelines for Selecting a Multiple Comparsisons Method in ANOVA
Tukey - Equal - Pairwise
Bonferroni - Equal or Unequal - Pairwise or general contrasts
Scheffe - equal or unequal - general contrasts
Tukey method has the smallest width (most confidence)
Bonferroni has the smaller width (less confidence)
Scheffe has the smallest width (least confidence)
9.4 - The Randomized Block Design
Randomized block design uses experimental units that are matched sets (blocks)
What is the procedure?
Matched sets of experimental units called blocks are formed, each block consists of k experimental units (k is the number of treatments).
One experimental unit from each block is randomly assigned to each treatment, resulting in a total of n = bk responses
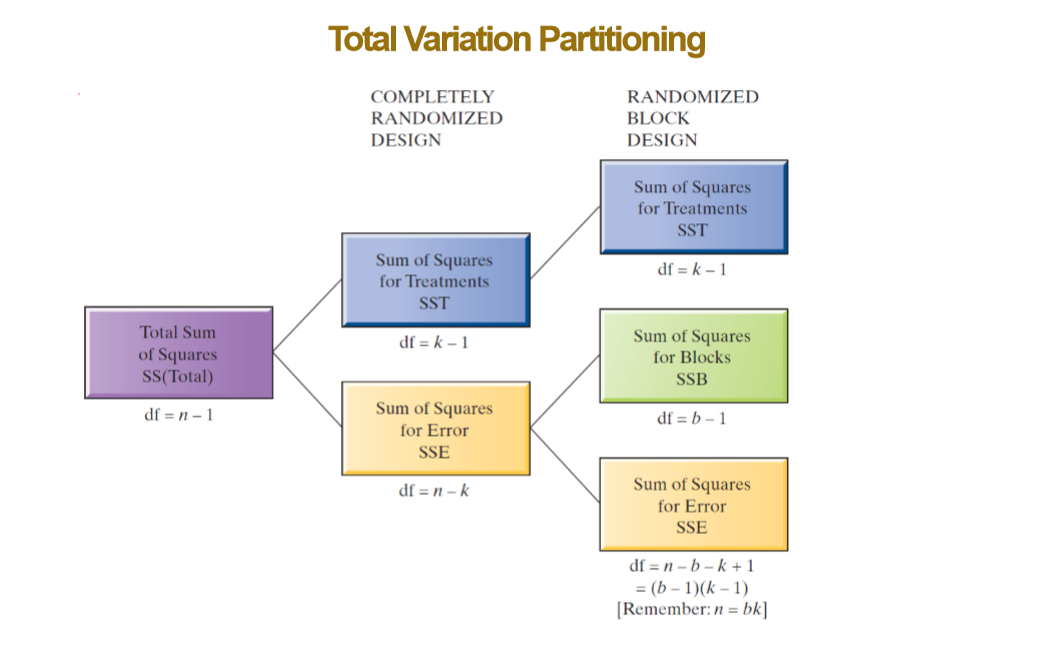
Use ANOVA test to compare k treatment means of randomized block designs
Conditions Required:
The b blocks are randomly selected, and all k treatments are applied
The distributions of observations corresponding to all bk block-treatment combinations are approximately normal
The bk block-treatment distributions have equal variations
If the treatment means are not equal, we then use the multiple comparrisons proceedure:
c = k(k-1)/2
If the treatment means differ, use Tukey or Bonferroni to find pairs of means
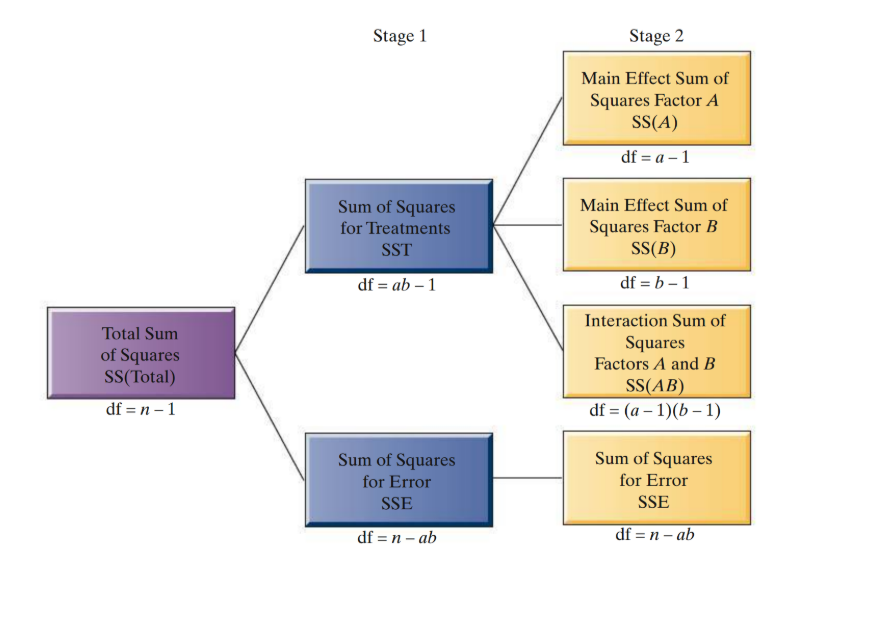
9.5 - Factorial Experiments: Two Factors
A complete factorial experiment is one in which every factor-level combination is employed
the number of treatments in the experiment equals the total number of factor-level combinations
The factorial experiment is often referred to as a two-way classification
Factor interation is used to test whether the factors combine to affect the response
Factor main effect components are used to determine whether the factors separately affect the response
Steps:
Chapter 10: Categorial Data Analysis
10.1 - Categorial Data and the Multinomial Experiment
What are the properties of the multinomial experiment?
The experiment consists of n identical trials
There are k possible outcomes to each trial. These outcomes are called classes, categories, or cells
The probabilities of k outcome, denoted by p1 + p2…… pk
The trials are independent
The random variables of interest are the cell counts
10.2 - Testing Category Probabilities: One-Way Table
10.3 - Testing Category Probabilities: Two-Way Contigency Table
One-way table because a single variable is used
Chi-Square Test measures the degree of disagreement between the data and the null hypothesis
What are the conditions required for a valid chi square test?
A multinomial experiment has been conducted. This is generally by taking a random sample.
The sample size must be large