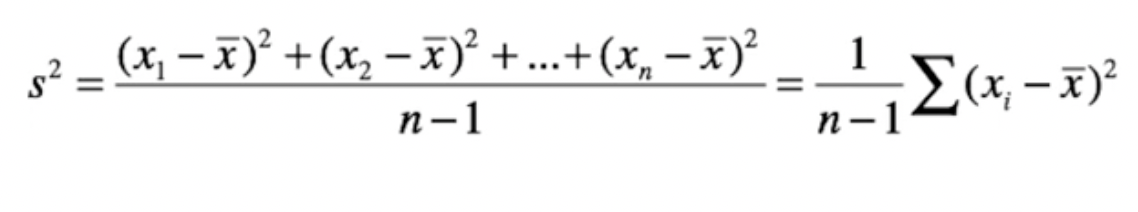1.2: Histograms, Box Plots, Outliers, and Standard Deviation

Introduction to Histograms

• Histogram: a bar graph for quantitative data
• The horizontal axis is divided into classes
• Each class needs to cover the same range of values
• Generally, 5-7 classes is a good minimum
• The more classes, the more detail/nuance shown
• The vertical axis measures how much data is in each class
• The bars must be touching
• If a data point is on the break of a class group (on a tick mark on the x-axis), it is included in the right bar
• Frequency histogram: a histogram showing the number of data points
• Relative frequency histogram: a histogram showing the percent of data
  • Can be made by taking the frequency in each class and dividing it by the total number of data points
• The center is generally found by estimation, especially if only a graph is given
• A histogram displays how many pieces of data are in each class

Histograms must have

• Consistent scales on both axes
• Labels for both axes
• A break on the x-axis if it does not start at 0
• The y-axis starting at 0

Outliers

• Data points are considered outliers if they lie…

  

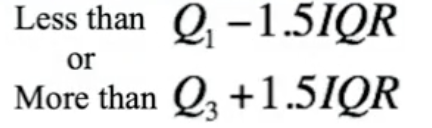
• Eg. data set: 18, 19, 13, 2, 15, 19, 15, 31, 17, 16, 29

  • Q1 = 15
  • Q3 = 19
  • IQR = Q3 - Q1 = 4
  • Q1 - 1.5(IQR) = 15 - 1.5(4) = 9 → anything below 9 is an outlier
  • Q3 + 1.5(1QR) = 19 + 1.5(4) = 25 → anything above 25 is an outlier
  • So, 2, 29, and 31 are outliers

Choosing Relevant Measurements

Mean and Standard Deviation

• Mean is the numerical standardized average of a set of data
• Standard deviation is the spread of data about the mean
• Standard deviation uses the same units as the original data
• Skew and outliers influence both mean and standard deviation
  • Skew: the extent to which a graph is pulled to one side or centered around the middle
  • If skew/outliers are present in a data set, this means that mean and standard deviation should not be used
• These measurements work well when data is approximately symmetrical with no outliers

Median, Quartiles, Range, and IQR

• Resistent to outliers
• These measurements work well when data is skewed and/or contains outliers

Measuring the Spread of Data

• Range = maximum - minimum
• IQR = Q3 - Q1
• Standard Deviation
  • 
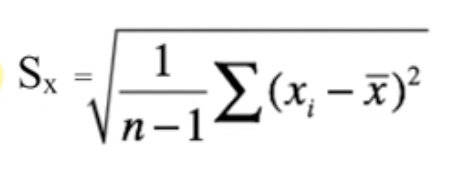
  • x̄ = mean
  • Standard deviation measures the rough average distance between each point and the mean
  • Larger standard deviations indicate that there is more data further from the mean
  • Moderate standard deviations indicate that data is moderately spread around the mean
  • Smaller standard deviations indicate that there is more data clumped closer to the mean
• Variance
  • 
• Variance is also equal to the square root of standard deviation
• Remember to always plot data; measures of spread and center only display specific facts about a data set, but graphs give the best overall pictures of distributions

\