7.1: Statistics and Parameters

Statistics and Parameters

• Statistic: a number that describes some characteristic of the sample
  • Relevant symbols
  • Mean: x̄
  • Proportion: p̂
  • Standard deviation: S
• Parameter: a number that describes some characteristic of the population
  • Relevant symbols
  • Mean: μ
  • Proportion: p
  • Standard deviation: σ
• Samples are taken to try to estimate the population (μ or p)
• Ultimate goal: Estimate parameters based on statistics

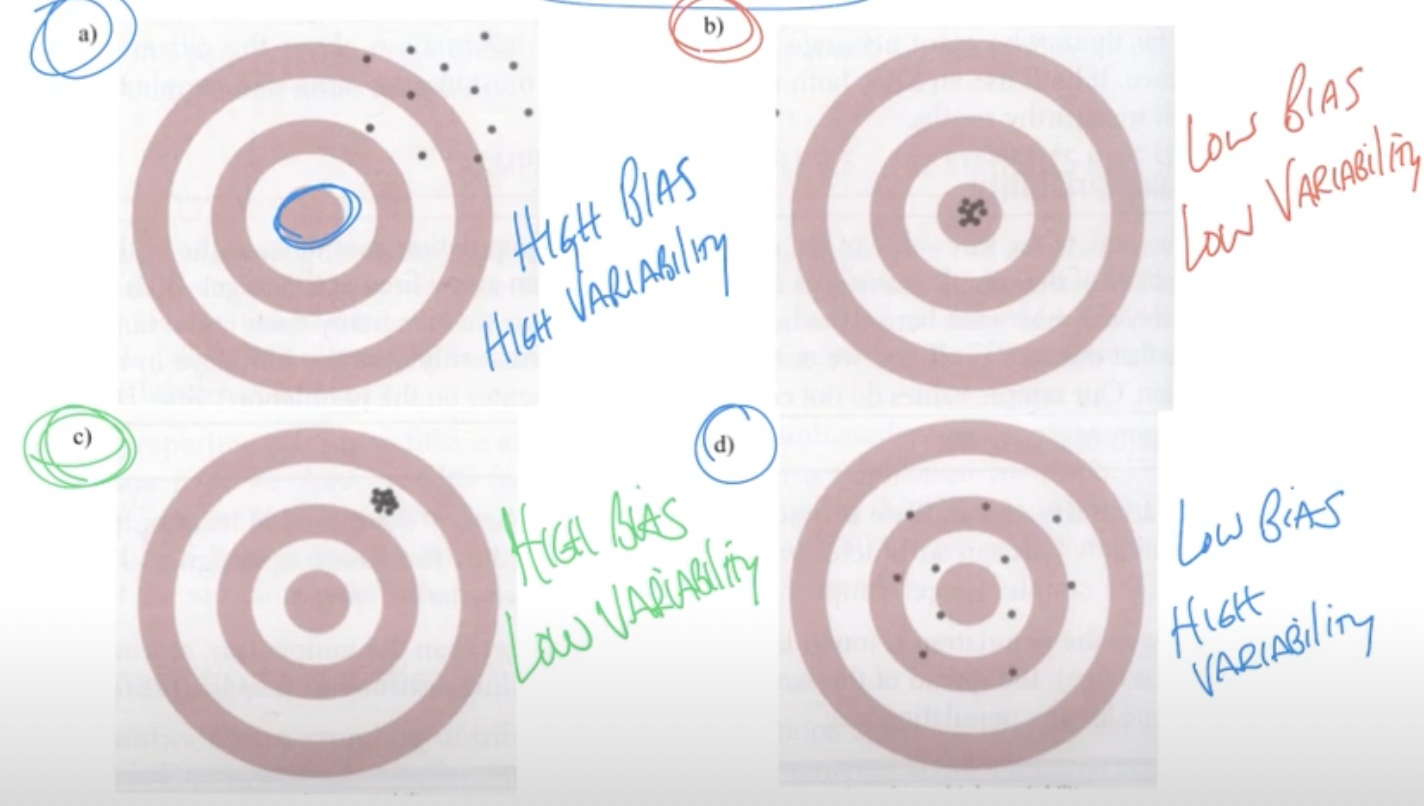
Distribution, Variability, and Bias

• Sampling distribution: the distribution of values taken by the statistic in all possible samples of the same size from the same population
  • Eg. sample mean, proportion
• Sampling variability: how much results vary between samples
  • Every time a sample is taken, the results will vary
  • Measured using the spread of the random sample
  • Based primarily on the size of the random sample
• As a general rule of thumb,
  • Larger sample: less variability
  • Smaller sample: more variability
• The spread does not depend on the size of the population, as long as it is at least 10x larger than the sample
• Biased statistic: a statistic which consistently overestimates or underestimates the parameter (mean or proportion)
• Unbiased statistic: a statistic in which the distribution of samples is centered around the true population’s parameter

Bias vs. variance

Means and Proportions

• Proportion problems generally involve categorical variables

• Binomial distributions will become approximately normal distributions if np≥10 and n(1-p)≥10

  • n = sample size
  • p = population proportion
  • p̂ = sample proportion
  • Normal distribution means the use of z-scores as a standard measure

  

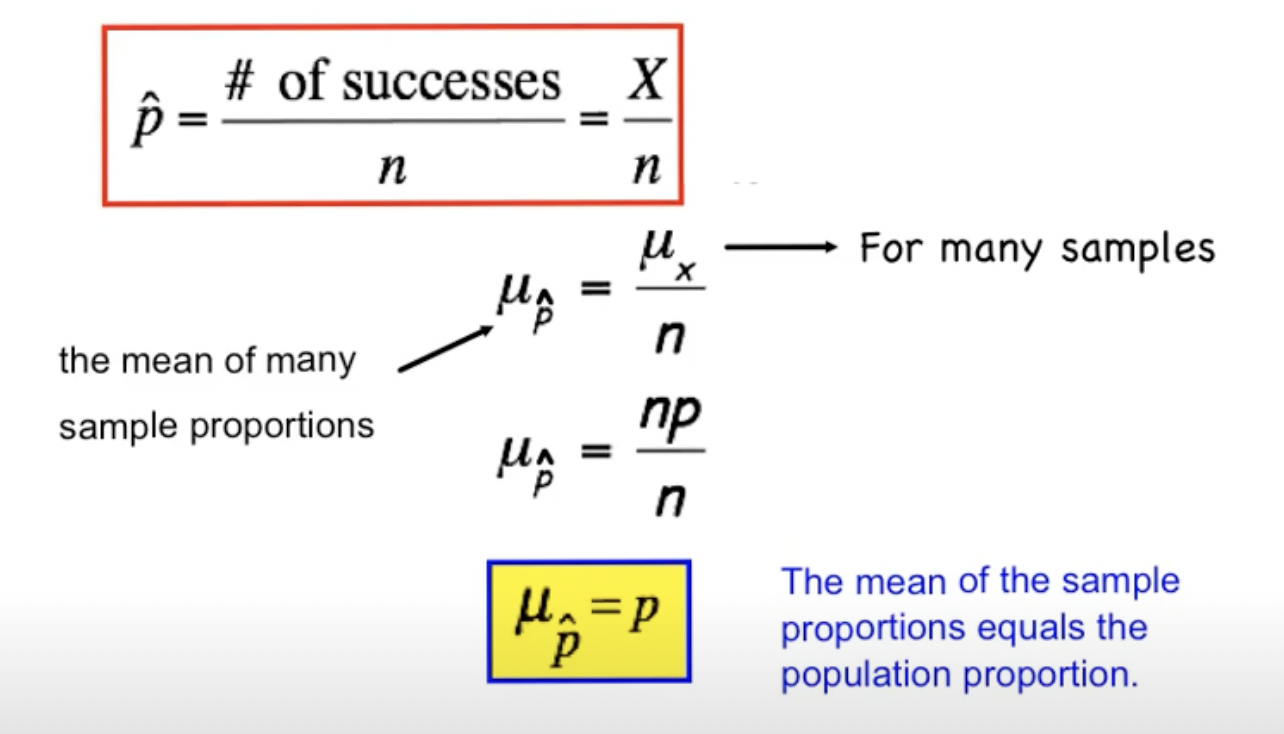
• Statistics are unbiased if they are equal to the true parameters, so p̂ is an unbiased estimator of p

Verifying Conditions

• If an SRS is taken of size n from a large population with proportion p,
  • Some conditions must be stated and checked
  • Is the population more than 10x larger than the sample size?
    • The 10% condition verifies that the standard deviation formula may be used
  • Is np ≥ 10 and is n(1-p) ≥ 10?
    • This verifies that a normal approximation may be used
• If these conditions are met, the mean of the sample proportions will equal the true population proportion

\