Biostatistics, Chapters I & II

Sampling

• Population: complete collection of all measurements or data that are being considered.
• Sample: sub-collecion of members selected from a population
• Simple Random Sample: each member of the population has the same change of being included, and samples are chosen independently
• Cluster Sampling: dividing the population into groups by a category. All of the individuals within the single group are the sample.
• Stratified Random Sampling: divide the population into groups (strata) based on one+ classification criteria. Then perform a simple random sample within each strata
• Sampling Bias: some members of the population have a higher chance to be selected than others.

Variables

• Categorical Variables: two+ categories, but no intrinsic ordering (ex: blood type)
• Ordinal Variable: categorical variables but with a clear ordering (small/medium/large)
• Numeric Variables
  • Discrete Variables: a numeric variable for which we can list the possible values (think: integers)
  • Continuous Variable: a numeric variable that is measured on a continuous scale (temperature, height)
• Bar Charts: frequency distribution for categorical variables
• Histograms: frequency distribution but no spaces

Frequency Variables

• Mean, denoted by ȳ
  • Mean: The average of the observations
  • Only for discrete or continuous data
  • ȳ = (Σ yi)/(n)
  • Sensitive to outliers
• Median, denoted by ỹ
  • N is odd: (n + 1)th largest value
  • N is even: average of (n/2)th largest value and (n/(2) + 1)th
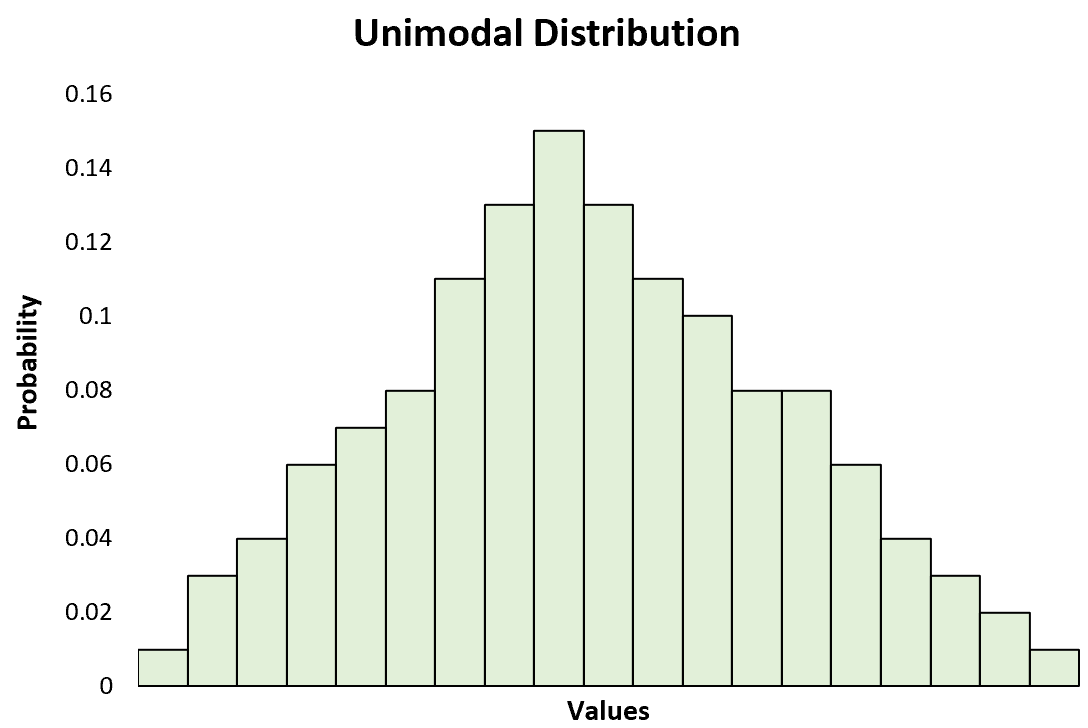
• Symmetric and Unimodal Curve
  • 
• Symmetric and Multimodal Curve
  • 

Box Plots

• Quartiles
  • Q1 = 25th Percentile
  • Q2 = 50th Percentile (Median)
  • Q3 = 75th Percentile
• Fences
  • LF = Q1 - h
  • UF = Q3 + h
  • h = 1.5(Q3 - Q1)
  • Outliers are any points that lie outside of the LF and UF
• Drawing a Box Plot
  • Central box from Q1 to Q3
  • Line in the middle is Q2
  • Whiskers extend to the point CLOSEST to the LF & UF (not the actual values of the fences)
  • Outliers are marked by small circles

Label y axis

Variance

• Sample variance
  • s^2 = Σ(yi - ȳ)^2 / n - 1
  • Remember to subtract one from n
• Simple Standard deviation
  • Sqrt(s^2)
  • Same unit as the original data value
• \

\