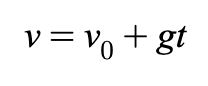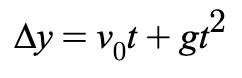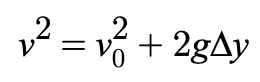Physics Enrichment | Formula List

Variables

• V = vector

• V_x = horizontal component of a vector

• V_y = vertical component of a vector

• R = magnitude of resultant vector

• R_x = horizontal component of a resultant vector

• R_y = vertical component of a resultant vector

• δ = angle of resultant vector

• ∆x = horizontal displacement

• ∆y = vertical displacement (for free-fall, can also be represented by d)

• x₀/x_i = initial position

• x/x_f = final position

• ∆t = change in time

• t₀/t_i = initial time

• t/t_f = final time

• v_avg = average velocity

• ∆v = change in velocity

• v₀/v_i = initial velocity

• v/v_f = final velocity

• a = acceleration

• g = gravity = -9.8 m/s²

Equations for Variables

Displacement

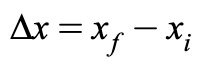
Change in Time

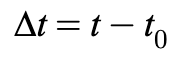
Average Velocity

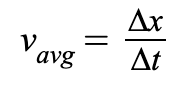
Change in Velocity

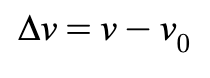
Acceleration

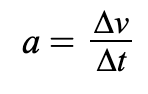
Finding Components of a Vector (V)

Horizontal Component

• V_x = |V| • cos(ϴ)

Vertical Component

• V_y = |V| • sin(ϴ)

Resultant Vector

Component Form of a Vector

• V = V_x^i + V_y^j

  • ^i is the unit vector along the x-axis.

  • ^j is the unit vector along the y-axis.

Adding Components

• R_x = ∑ V_x (add the horizontal or x-components of all individual vectors)

• R_y = ∑ V_y (add the vertical or y-components of all individual vectors)

Magnitude of the Resultant vector

• R = √R_x² + R_y²

Angle of the Resultant Vector

• δ = tan^-1 (R_y/R_x)

Kinematics Equations

Equation 1

• describes how velocity changes over time when acceleration is constant

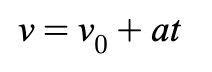
Equation 2

• describes the position of an object at any time, considering both initial velocity and acceleration

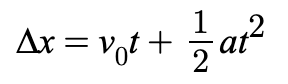
Equation 3

• relates velocity and displacement without time

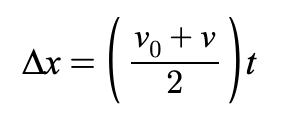
Equation 4

• describes position based on average velocity

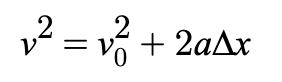
Free Fall Equations