Chapter 1: Units, Physical Quantities, and Vectors

STUDY KEY🔑: ==Sections==, ^^Sub-Sections^^, Keywords, %%Examples%%

==1.1 The Nature of Physics==

• Physics observes the phenomena of nature and tries to find patterns and principles that relate to these phenomena

• These patterns can be called Physical theories or if they’re well established they are known as Physical laws or principles

• The development of physical theory requires creativity at every stage %%(Ex. Asking appropriate questions, designing experiments to try to answer those questions, and drawing appropriate conclusions from the results)%%

• No theory is ever regarded as the final truth. There is always a possibility that new observations will require a theory to be revised or discarded

  \

==1.2 Solving Physics Problems==

There are four stages to solving a physics problem (ISEE)

1. Identify
2. Set up
3. Execute
4. Evaluate

\
IDENTIFY (the relevant concepts:)

What physics ideas are relevant to the problem? At this stage, you must identify the target variable of the problem - that is, the quantity whose value you’re trying to find. (%%Ex. The speed at which a projectile hits the ground, the intensity of a sound made by a siren, the size of an image made by a lens, etc.)%%

\
SET UP (the problem:)

Based on the concepts you selected in the Identify step, choose the equations you’ll use to solve the problem and how you’ll use them. %%(Ex. Make a sketch of the situation described in the problem)%%

\
EXECUTE (the solution:)

Make a list of all known and unknown quantities, and note which are the target variable or variables. Then solve the equations for the unknowns.

\
EVALUATE (your answer:)

Examine your answer to see what it’s telling you. Ask yourself, “Does this answer make sense?” Go back and check your work, and revise your solution as necessary.

\

^^Idealized Models^^

• A model in physics is a simplified version of a physical system that would be too complicated to analyze in full detail %%(Ex. Let’s say we want to analyze the motion of a thrown baseball Fig. 1.2a)%%

  In Fig. 1.2b you can see the Idealized Model of the baseball

  

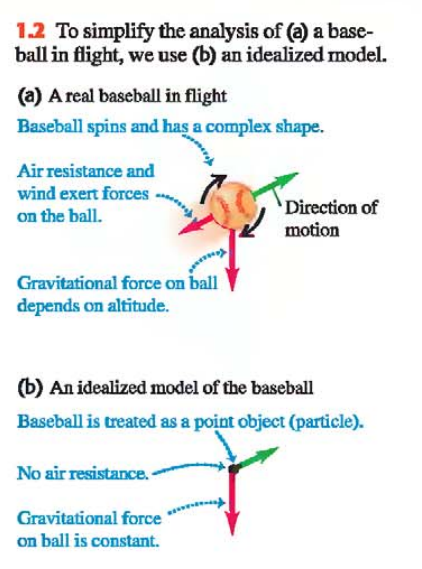
• When we use a model to predict how a system will behave, the validity of our predictions is limited by the validity of the model

• When we apply physical principles to complex systems in physical science, we always use idealized models

• The principles of physics themselves are stated in terms of idealized models %%(Ex. When we speak about point masses, rigid bodies, ideal insulators, etc.)%%

\

==1.3 Standards and Units==

• Any number that is used to describe a physical phenomenon quantitatively is called a physical quantity %%(Ex. Two physical quantities that describe you are your weight and your height)%%

• Some physical quantities are so fundamental that we can define them only by describing how to measure them. This definition is called Operational Definition. %%(Ex. Two examples are measuring a distance by using a ruler and measuring a time interval by using a stopwatch)%%

• When we measure a quantity, we always compare it with some reference standard. (%%Ex. When we say that a Porsche Carrera GT is 4.61 meters long, we mean that it is 4.61 times as long as a meter stick)%% this standard defines a unit of the quantity

• The system of units used by scientists and engineers around the world is commonly called “the metric system“ but since 1960 it has been known officially as the International System or SI

  

\

^^Time^^

• From 1889 until 1967, the unit of time was defined as a certain fraction of the mean solar day, the average time between successive arrivals of the sun at its highest point in the sky.
• Today’s standard which was adopted in 1967, is based on an atomic clock. Which uses the energy difference between the two lowest energy states of the cesium atom. When bombarded by microwaves with the same frequency, cesium atoms undergo a transition from one of these states to the other.
• One second (s) is defined as the time required for 9,192,631,770 cycles of this microwave radiation

\

^^Length^^

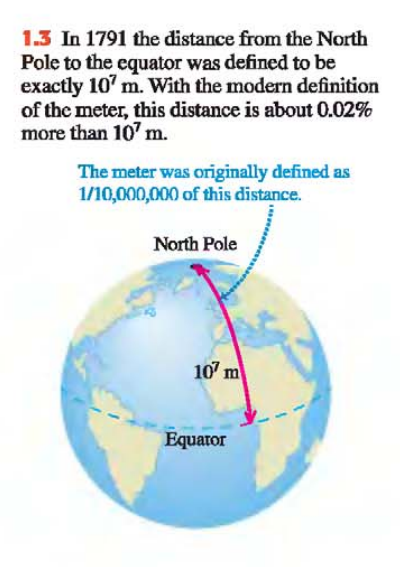
• In 1960 an atomic standard for the meter was also established, using the wavelength of the orange-red light emitted by atoms of krypton in a glow discharge tube.
• In November 1983, the length standard was changed again so that the speed of light in a vacuum was defined to be precisely 299,792,458 m/s
• The new definition of the meter (m) is the distance that light travels in a vacuum in 1/299,792,458 second.

\

^^Mass^^

• The standard of mass, the kilogram (kg) is defined to be the mass of a particular cylinder of platinum-iridium alloy kept at the International Bureau of Weights and Measures at Sevres, near Paris (Fig. 1.4)

  

\

^^Unit Prefixes^^

• Once we have defined the fundamental units, it is easy to introduce larger and smaller units for the same physical quantities.

• The names of the additional units are derived by adding a prefix to the name of the fundamental unit.

  %%(Ex. The prefix “kilo-“ always means a unit larger by a factor of 1000; thus%%

  %%1 kilometer = 1 km = 10³ meters = 10³ m%%

  %%1 kilogram = 1 kg = 10³ grams = 10³ g%%

  %%1 kilowatt = 1 kw = 10³ watts = 10³ w)%%

  

  

  

^^The British System^^

• These units are used only in the United States and a few other countries, and in most of these, they are being replaced by SI units.

British units are now officially defined in terms of SI units, as follows:

Length: 1inch = 2.54 cm (exactly)

Force: 1 pound = 4.448221615260 newtons (exactly)

\

==1.4 Unit Consistency and Conversions==

• We use equations to express relationships among physical quantities, represented by algebraic symbols
• Each algebraic symbol always denotes both a number and a unit, %%(Ex. d might represent a distance of 10m, t a time of 5s, and v a speed of 2 m/s)%%
• An equation must always be dimensionally consistent. You can’t add apples and automobiles; two terms may be added or equated only if they have the same units. %%(Ex. If a body moving with constant speed v travels a distance d in a time t, these quantities are related by the equation d=vt)%%

\

^^Problem-Solving Strategy | Unit Conversions^^

IDENTIFY (the relevant concepts:)

Unit conversion is important, but it’s important to recognize when it’s needed. In most cases, you're best off using the fundamental SI units (lengths in meters, masses in kilograms, and time in seconds)

\
SET UP (the problem) and EXECUTE (the solution:)

Units are multiplied and divided just like ordinary algebraic symbols. This gives us an easy way to convert a quantity from one set of units to another. %%(Ex. When we say that 1 min = 60s, we don’t mean that 1 min represents the same physical time interval as 60s.)%%

\
EVALUATE (your answer:)

If you do your unit conversions correctly, unwanted units will cancel. To be sure you convert units properly, you must write down the units at all stages of the calculation. Finally, check whether your answer is reasonable.

\
%%Example: Solving a problem using Problem Solving Strategy | Unit Conversions%%

\

==1.5 Uncertainty and Significant Figures==

• Measurements always have uncertainties. If you measure the thickness of the cover of this book using an ordinary ruler, your measurement is reliable at only the nearest millimeter, your result will be 3 mm; this would be wrong. But if you use a micrometer caliper, a device that measures distances reliably to the nearest 0.01 mm, the result would be 2.91 mm. The distinction between these two measurements is in their uncertainty.
• The uncertainty is also called the error because it indicates the maximum difference there is likely to be between the measured value and the true value.
• We often indicate the accuracy of a measured value - that is, how close it is likely to be to the true value - by writing the number, the symbol (±), and a second number indicating the uncertainty of the measurement. %%(Ex. If the diameter of a steel rod is given as 56.47 ± 0.02 mm, this means that the true value is unlikely to be less than 56.45 mm or greater than 56.49 mm)%%
• We can also express the accuracy in terms of the maximum likely fractional error or percent error (also known as fractional uncertainty and percent uncertainty)

In many cases, the uncertainty of a number is not stated explicitly. Instead, the uncertainty is indicated by the number of meaningful digits, or significant figures, in the measured value. %%(Ex. We gave this book cover a thickness of 2.91mm, which has three significant figures. By this we mean that the first two digits are known to be correct, while the third digit is uncertain.)%%

\
%%Example: Using Significant Figures%%

• When we calculate with very large or very small numbers, we can show significant figures much more easily by using scientific notation, sometimes called powers-of-10 notation.
• It is important to note that precision is not the same as accuracy. %%(Ex. A cheap digital watch that gives the time as 10:35:17 a.m. is very precise, but if the watch runs several minutes slow, then this value isn’t very accurate. On the other hand, a grandfather clock might be very accurate, but if the clock has no second hand, it isn’t very precise.)%%

\

==1.6 Estimates and Orders of Magnitude==

• Sometimes we may need to guess at the data we need for the calculation. Or the calculation might be too complicated to carry out exactly, so we make some rough approximations. Such calculations are often called order-of-magnitude estimates

  \

%%Example: An order-of-magnitude estimate%%

\

==1.7 Vectors and Vector Addition==

• Some physical quantities, such as time, temperature, mass, and density, can be described completely by a single number with a unit. But many other important quantities in physics have a direction associated with them and cannot be described by a single number. %%(Ex. To describe the motion of an airplane completely, we must say not only how fast the plane is moving, but also in what direction.)%%

• When a physical quantity is described by a single number, we call it a scalar quantity. In contrast, a vector quantity has both a magnitude ( the “how much“ or “how big“ part) and a direction in space.

• Calculations that combine scalar quantities use the operations of ordinary arithmetic. %%(Ex. 6kg + 3kg = 9kg, or 4 x 2s = 8s)%%

• To understand more about vectors and how they combine, we start with the simplest vector quantity, displacement. Displacement is simply a change in position of a point. %%(Ex. Fig. 1.9a)%%

  

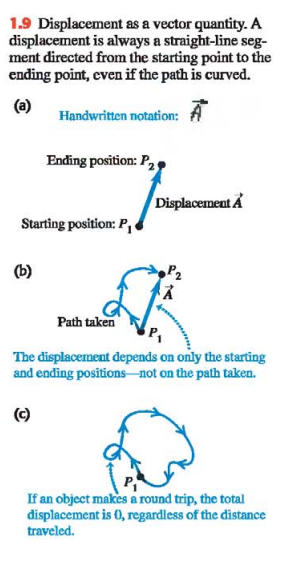
• If two vectors have the same direction, they are parallel. If they have the same magnitude and the same direction, they are equal, no matter where they are located in space.

• We define the negative of a vector as a vector having the same magnitude as the original vector but in the opposite direction

\
%%Example: The negative of a vector%%

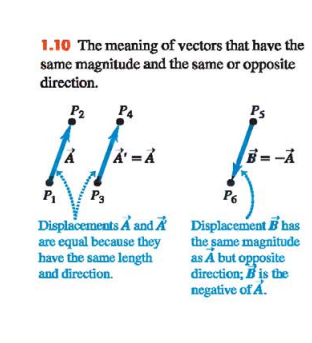
• When two vectors have opposite directions, whether their magnitudes are the same or not, we say that they are antiparallel.

\

^^Vector Addition^^

• In (Fig. 1.11a) we call displacement C the vector sum, or resultant, of displacements A and B.

  

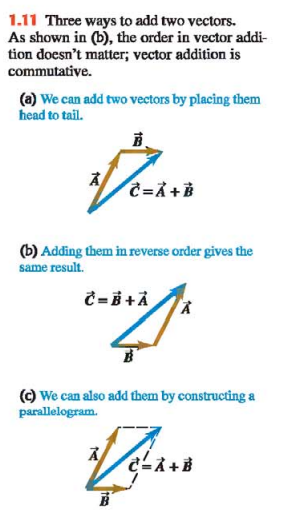
• If we make the displacements A and B in reverse order, with B first and A second, the result is the same (Fig. 1.11b)

• This shows that the order of terms in a vector sum doesn’t matter. In other words, vector addition obeys the commutative law.

\

==1.8 Components of Vectors==

• A simple but general method for adding vectors is called the method of components

• In (Fig. 1.17a) the vectors labeled A(x) and A(y) are called the **component vectors **of vector A→ and their sum is equal to A→.

  

\
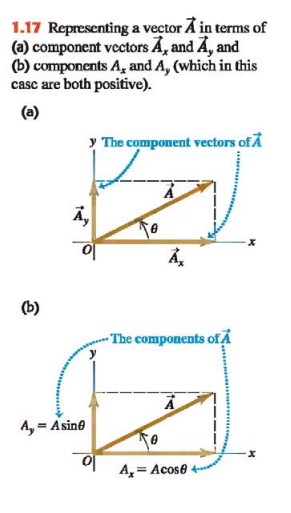
%%Example: Finding Components%%

\

^^Doing Vector Calculations Using Components^^

• Using components makes it relatively easy to do various calculations involving vectors. Below are three examples.

1. Finding a vector’s magnitude and direction from its components

We can describe a vector completely by giving either its magnitude and direction or its x- and y- components. %%(Ex. Equation 1.6 shows how to find the components if we know the magnitude and direction.)%%

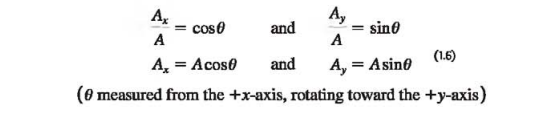
We can also reverse the process: We can find the magnitude and direction if we know the components. By applying the Pythagorean theorem to Fig. 1.17b (above in section 1.8), we find the magnitude of vector A→ is.

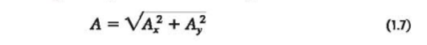
If Ø is measured from the positive x-axis, and a positive angle is measured toward the positive y-axis as in Fig. 1.17b (above in section 1.8), then

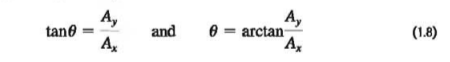
2. Multiplying a vector by a scalar

\