Chapter 8- Potential Energy and Conservation of Energy

INTRODUCTION TO PHYSICS (8)

• One purpose of physics is also to recognise the types of energy in the world.
• One of the most common energies is the potential energy, U.
• Potential energy is basically the energy stored in a system depending on their relative position.
• Physics is used to calculate the potential energy in an object so it can be used effectively, for e.g. during bungee jumping, the right cord used is determined by the amount of potential and elastic energies.

WORK AND POTENTIAL ENERGY

• If an object is thrown upward, work done on the object by the gravitational force is negative because the force transfers energy from the kinetic energy of the object.
• This energy is transferred by the gravitational force to the gravitational potential energy of the object–Earth system.
• When the object has reached its maximum height and begins to fall downwards again, the transfer of energy is reversed.
• Work done on the object by the gravitational force is now positive—that force transfers energy from the gravitational potential energy of the object–Earth system to the kinetic energy of the object.
• During all conditionst, the change in potential energy is equal to the negative work done on the object.
• This principle also works in horizontal conditions.

CONSERVATIVE AND NON-CONSERVATIVE FORCES

• A conservative force is a force with the property that the total work done in moving a particle between two points is independent of the path taken, e.g. spring force and gravitational force.
• A non-conservative force is the opposite of the conservative force, i.e.a force for which work depends on the path taken, e.g. drag force and kinetic friction.
• When only conservative forces act on a particle-like object, we can greatly simplify otherwise difficult problems involving the motion of the object.
• It is to be remembered that a force acts between a particle-like object in the system and the rest of the system.
• Work is done when the configuration of the system is changed. The work done is also reversed when the configuration is reversed.

IDENTIFYING CONSERVATIVE AND NON-CONSERVATIVE FORCES

• For this primary test, it is important for the particle to move along a closed path, i.e. it must start and end at the same initial position.
• If the energy transferred to and from the particle is zero, the force is conservative.
• In terms of work, we can say that the work done on a particle by a conservative force along a closed path is zero.
• This also proves the above-mentioned fact that the work done by a conservative force on a particle is independent of the path taken by the particle.

DETERMINING POTENTIAL ENERGY VALUES

• Before moving onto more complex things like deriving equations of gravitational potential energy and elastic potential energy, first we have to find a general relation between the conservative force and the associated potential energy.

• If we take the conservative force on a particle as F, the potential energy is the negative of the work done (U=-W)

• In most cases when the force varies with position, the work done can be written as the integral of the force where xi and xj are initial and final positions of the object respectively.

  

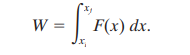
• Since the potential energy is the negative of work done, it can be written as

  

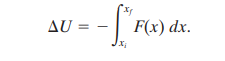
• While finding the change in gravitational potential energy, there are two changes done in the integral above.

• Since the gravitational potential energy is a vertical force, integration is done on the y-axis instead of the x-axis with yi and yj as the initial and final positions.

• The force F is substituted with mg.

  

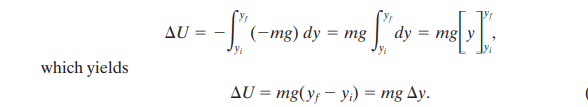
• To simplify things, we often say that at a certain height, a certain gravitational potential energy U is associated with the object-earth system.

  

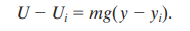
• When U is taken to be the G.P.E in a reference configuration with y as a reference point, Ui and yi is taken as 0. This gives us:

  

• This equation tells us that the G.P.E of an object-Earth system depends on the verticle position y or the height relative to its reference point y=0, and not on the horizontal position.

\

ELASTIC POTENTIAL ENERGY

• If we imagine a block at the end of a spring moving from position xi (when spring is relaxed) to position xy (as the spring stretches), we already know from previous chapters that the force F does work (F=-kx).

• To find the elastic potential energy, the force F(x) can be substituted by -kx, wich gives us:

  

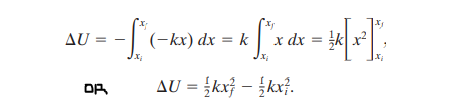
• To associate potential energy value U with it, the spring is considered to be at its original length with the box at position xi=0. Then the G.P.E U is given by:

  

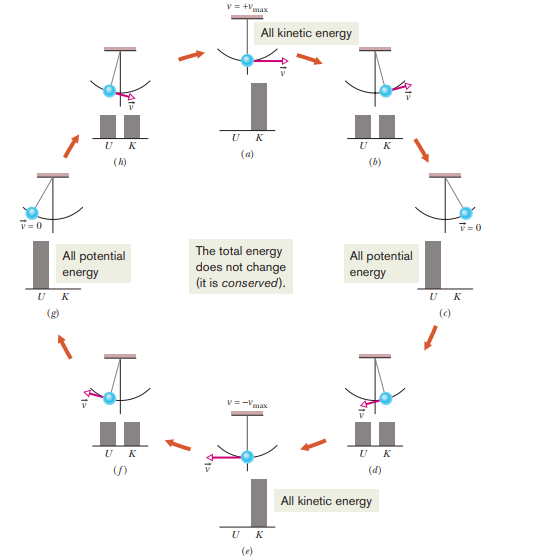
CONSERVATION OF MECHANICAL ENERGY

• The mechanical energy of an object, Emee is the sum of the kinetic energy K and the gravitational potential energy U of an object.

  

• The question here is what happens to mechanical energy when energy transfer occurs within a system, but the energy transfer here is caused only by conservative forces.

• It will be assumed that the system is isolated.

• Since kinetic energy is equal to the work done, and the potential energy is equal to the negative of the work done, it is observed that the energy lost is equal to the energy gained, therefore the mechanical energy is conserved.

• It can be said that in an isolated system where only conservative forces cause energy changes, the kinetic energy and potential energy can change, but their sum, the mechanical energy Emec of the system, cannot change.

• This is called the principle of conservation of mechanical energy (and is also from where conservative forces get their name!)

  

READING A POTENTIAL ENERGY CURVE

• We know how to find the G.P.E when we know the force F. Now we will go the opposite way, i.e. find the force when we know the G.P.E.

• For a 1D motion, the G.P.E is equal to the negative of the work done which is equal to the negative force into the change in distance.

• To solve for F(x) in a differential limit yield, it can be written as:

  

  \

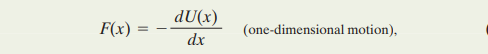
• Force can also be graphically found.

  

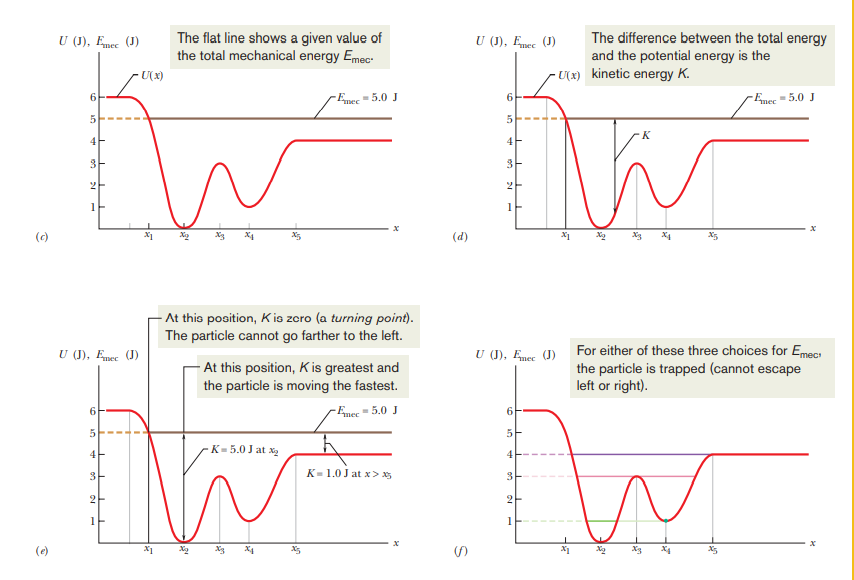
EQUILIBRIUM POINTS

• When the potential energy of a system is equal to its mechanical energy, the system has 0 kinetic energy which means it’s stationary. This position of the particle is known as neutral equilibrium.
• When the particle is at exactly the turning point such that is starts to move if displaced even slightly, the position of the object is said to be unstable equilibrium.
• A particle that cannot move left or right because it requires a negative K.E, and a restoring force is needed to move it, the position of the particle is called stable equilibrium.

WORK DONE ON A SYSTEM BY AN EXTERNAL FORCE

• It is already known that work is the transfer of energy due to a force. This force is an external force specifically.
• Normally only the kinetic energy is changed while other forms of energy remain unaffected by external forces during work. However, some systems are more complicated and may have changes in other forms of energy as well, such as potential energy.
• When friction is not involved: Imagine throwing a ball upward. As the ball rises, it gains kinetic energy (as it moves from its stationary position). As it rises upwards, there is also an increase in the gravitational potential energy of the ball-earth system.
• This gives the total work done as the sum of change in kinetic energy and the change in potential energy. Since the sum of change in kinetic energy and the change in potential energy is equal to the total mechanical energy of the system, we can say that the work done is equal to the total change in mechanical energy of the system.
• When friction is involved: Imagine a block being slid across a horizontal surface (the x-axis) by a constant force F. A constant frictional force opposes it, and as it covers some displacement d, its velocity also changes to a constant non-zero value from zero. Since forces are constant, acceleration is also constant. Thus the equation

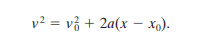
can be written as

• If this equation is solved for a and then substituted into F=ma where F is the resultant force (F-Fk where Fk is the kinetic frictional force), it can be rearranged to give us:

  

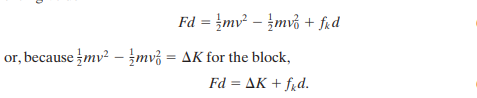
• Since in some situations where height is involved (e.g. in a block moving up a ramp instead of horizontally), there may also be a change in the potential energy. Therefore, the equation is generalised as:

• As the block moves, there is friction between it and the floor which causes the block and floor to become warmer. This is the increase in their thermal energy, Eth.

• Through experiments, it is known that the change in thermal energy is equal to the product of kinetic frictionalforce and the distance moved (Fkd).

• Therefore, the equation above can also be written as:

  

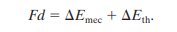
which is the work done when friction is involved.

\

CONSERVATION OF ENERGY

• The law of conservation of energy states that energy cannot appear or disappear, and even when work is done, the total mechanical energy of the system remains the same.

• Since the only energy transfer discussed yet is work done, the law can be written in an equation as

  

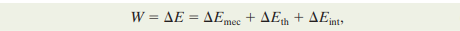
where ΔEmec is any change in the mechanical energy of the system, ΔEth is any change in the thermal energy of the system, and ΔEint is any change in any other type of internal energy of the system. Included in ΔEmec are changes ΔK in kinetic energy and changes ΔU in potential energy (elastic, gravitational, or any other type we might find).

• However, if the system is isolated, i.e. there can be no energy transfer to or from it, the law of conservation states that the total energy of an isolated system is constant, even though there may be energy transfers within the system itself.
• In an isolated system, we can relate the total energy at one instant to the total energy at another instant without considering the energies at intermediate times.
• Now that energy has been described in more detail, we can also say that power is the rate at which energy is transferred from one form to another by a force. Power can be written as the change in energy over change in time of energy transfer.
• Instantaneous power due to a force is the derivative of energy over the derivative of time.

\