math revision T03 and T04

TOPIC 3: PYTHAGORAS, SURDS AND INDICES

W1AB: Working with Surds:

Surds: numbers that can only be represented as a square root (e.g. \sqrt2, \sqrt7 )

Operations with surds: 3\sqrt2 = 3 x \sqrt2

Adding and subtracting - You can add and subtract ‘like surds’ (e.g. 3\sqrt2 and 5\sqrt2 )

e.g. 3\sqrt2 + 5\sqrt2 = 8\sqrt2

Multiplying surds - Multiply the values inside the square roots

e.g. \sqrt{20} x \sqrt2 = \sqrt{40}

To multiply expressions such as 2\sqrt3 x 6\sqrt5 , you need to multiply the integers, and then the surds.

so 2\sqrt3 x 6\sqrt5 = 12\sqrt{15}

Dividing surds - \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}

e.g. \frac{\sqrt{10}}{\sqrt2}=\sqrt{\frac{10}{2}}=\sqrt5

Simplifying Surds: To simplify surds, you need to split them into factors, where one of them has to be a perfect square. Then, you can take it out of the surd, and put it as an integer next to the surd.

e.g. \sqrt{18} = 3\sqrt2

\sqrt{18}=\sqrt{9\cdot2}

3\sqrt2

If there is more than one factor that is a perfect square, then you need to use the larger one, so that simplifying is more simple.

Expressing surds as a square root of a positive integer: You need to square the integer, put it in a square root symbol, and multiply it with the surd.

e.g. 3\sqrt5 = \sqrt9\cdot\sqrt5 = \sqrt{45}

Types of numbers:

Real numbers(R) - All numbers on the number line are considered ‘real’ numbers

Rational numbers (Q) - All fractions which have an integer as both the numerator and the denominator

Any number with a recurring decimal is considered irrational.

Integers (Z) - All whole numbers that are either positive or negative

Natural numbers - Numbers used for counting

Squaring expressions: For squaring surds, you need to square the integer first and then the surd itself. The answer will be an integer most of the time.

W2AB: Pythagoras’ Theorem:

Exact value - The value must not be rounded off. It must be given as surds or fractions where necessary. If a question doesn’t specifically ask for a rounded off value then you should give an exact value

Square root - For square rooting, you need to consider that it might be positive or negative.

Squaring - Brackets make a huge difference. 3x² is different to (3x)². 3x² equals 3x², while (3x)² is equal to 9x².

If you are solving a question related to the shape or quantity of something (e.g. length, time, height), you must take the positive answer from the square root, since negative answers are infeasible. For this, you always need to write the explanation.

Hypotenuse and Pythagoras’ Theorem: The Hypotenuse is the longest side of a right-angled triangle, which is always opposite the right angle.

Pythagoras’ Theorem: c^2=a^2+b^{^2}

You can substitute the values of the two other sides into a and b, to find c, or you can substitute the values of any variables to find any side.

W3AB and W4AB: Further Surds and Pythagoras’ Theorem:

Estimating the value of surds: Find surds with perfect squares that are closest to the surd, and you have an estimate.

e.g. \sqrt{11}

\sqrt9<\sqrt{11}<\sqrt{16}

so 3<\sqrt{11}<4

Formula for cubes of surds = (\sqrt{a} )³ = a\sqrt{a}

If the side lengths of a right-angled triangle satisfy Pythagoras’ Theorem, then you know it’s a right-angle triangle.

W5AB: Index Laws:

Law 1: a^m x aⁿ = a^m+n

Law 2: a^m/aⁿ = a^m-n

Law 3: (x^m)ⁿ = x^mn

Law 4: a⁰ = 1

Law 5: (ab)^m = a^mb^m

Law 6: (a/b)^m = a^m/b^m

W6AB: Indicial Equations:

Multiplying decimals:

e.g. 0.2 × 0.3

Multiply the numbers as if they weren’t decimals

2 × 3 = 6

Divide the number by the total amount of decimal places in both numbers

0.2 × 0.3 = 0.06

Solving indicial equations:

e.g. 3^x = 9

3^x = 3²

x = 2

e.g. 1000^x+2 = 10000

(10³)^x+2 = 10⁴

10^3x-6 = 10⁴

3x-6 = 4

3x = 10

x = 10/3

W7AB: Negative indices:

a^-n = 1/aⁿ

e.g. 2^x = 1/16

2^x = 1/2⁴

2^x = 2^-4

x = -4

TOPIC 4: QUADRATIC ALGEBRA

W1AB: Factorising:

Factorising:

e.g.1 6a+ax

The common factor is a. Take a out from the expression’s terms.

= a(6+x)

e.g.2 6(x-2) + x(x-2)

(x-2) is the common factor.

= (6+x)(x-2)

e.g.3 3x(x−1) + 2(−1+x)

(-1+x) = (x-1)

= (3x+2)(x-1)

e.g.4 x(x−3) + x−3

x-3 on its own is multiplied by 1.

= (x+1)(x-3)

e.g.5 x(x−3) + 4(3−x)

Notice how (x-3) and (3-x) are not the same. Take -1 out as a common factor from the second bracket.

= x(x−3) − 4(−3+x)

= x(x−3) − 4(x−3)

= (x−3)(x−4)

Factorising by grouping:

e.g. 4x²−8x − 3x+6

= 4x(x−2) − 3(x−2)

= (x−2)(4x−3)

Factorising quadratic trinomials:

For Factorising expressions with the form x²+bx+c, you need to find factors of c that add to b.

Case 1: When c and b are positive, both factors are positive.

e.g. x²+8x+12

Factors of 12 that add to 8 = 2, 6

= x²+2x+6x+12

= x(x+2)+6(x+2)

= (x+2)(x+6)

SHORTCUT METHOD:

Factors of 12 that add to 8 = 2, 6

= (x+2)(x+6)

Case 2: When c is positive and b is negative, both factors are negative.

e.g. x²−10x+16

Factors of 16 that add to -10 = -8, -2

= x²-2x-8x+16

= x(x-2)-8(x-2)

= (x-8)(x-2)

SHORTCUT METHOD:

Factors of 16 that add to -10 = -8, -2

= (x-8)(x-2)

Case 3: When c is negative, use one negative factor.

e.g. x²+4x−12

Factors of -12 that add to 4 = -2, 6

= x²-2x+6x-12

= x(x-2)+6(x-2)

= (x+6)(x-2)

SHORTCUT METHOD:

Factors of -12 that add to 4 = -2, 6

=(x-2)(x+6)

Perfect squares:

a²+ 2ab + b² = (a + b)²

a²− 2ab + b² = (a − b)²

e.g. x²+8x+16

Using the rule, find the factors.

= x²+2(4)x+4²

a = x, b = 2

= (x+2)²

W2AB: More Factorising:

Common factors: Some expressions have common factors for all terms. If the coefficient of x is -1, take out -1 as a factor.

e.g. 2x²+12x+16

Take out 2 as a common factor

= 2(x²+6x+8)

= 2(x²+2x+4x+8)

= 2(x(x+2)4(x+2))

= 2(x+4)(x+2)

Difference of perfect squares (DOPS): (a-b)(a+b) = a²-b²

e.g. x²-9

Use the DOPS rule to find the factors.

= (x-3)(x+3)

DOPS Factorising using fractions:

e.g. x²-1/16

= x²-(1/4)²

= (x-1/4)(x+1/4)

Factorising without expanding:

e.g. (x+4)²-9

= (x+4)²-3²

= (x+4+3)(x+4-3)

= (x+7)(x+1)

W3AB: Factorising Non-Monic Quadratics:

Factorising ax²+bx+c:

e.g. 6x²+17x+5

a = 6, b = 17, c = 5

Find factors of ac that add to b = 15, 2

= 6x²+2x+15x+5

= 2x(3x+1)+5(3x+1)

= (2x+5)(3x-1)

Before factorising, find common factors for all terms in the expression.

W4AB and W5AB: Solving Quadratic Equations:

Null Factor Law: Everything multiplied by 0 is equal to 0. For the answer of an equation to be 0, one of the numbers/expressions must equal 0.

e.g. if ab = 0, then a, or b, or both must be 0.

NULL FACTOR LAW: if ab = 0, then a = 0 or b = 0

e.g.1. x(x-5) = 0

Either x = 0 or x = 5

e.g.2 4(x+1)(x-7) = 0

Divide both sides by 4. Remember, 0/4 = 0

(x+1)(x+7) = 0

x = -1 or x = 7

e.g.3 x²+6x+8 = 0

(x+2)(x+4) = 0

x = -4, -2

e.g.4 x²-x = 20

Make the equation equal to 0 by moving 20 to the LHS

x²+x-20 = 0

(x+5)(x-4) = 0

x = -5, 4

e.g.5 2x²+10x+12 = 0

Take out 2 as a common factor

2(x²+5x+6) = 0

2(x+3)(x+2) = 0

Ignore the 2

x = -3, -2

You can also divide the equation by 2 at the beginning.

If the common factor is -1, you need to divide by -1 at the beginning.

For finding x for expressions such as 3x-2, you need to bring the 2 to the other side (3x = 2), and then divide the 2 by 3 (x = 2/3).

W6AB: Forming and Solving Quadratic Equations:

e.g. a) Write down an expression, in terms of x, for the area of this rectangle:

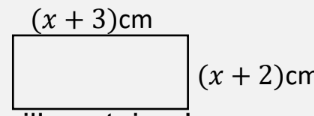
(x+3)(x+2) ← no need to expand now

b) If the area of the rectangle is 20cm², form an equation and solve it to find the value of x.

(x+3)(x+2) = 20

Expand the expression now

x²+5x+6 = 20

x²+5x-14 = 0

(x+7)(x-2) = 0

x = -7,2

Remember that things such as time, distance and speed don’t have a negative value, so the only option that you can choose here is x = 2. Don’t forget to cross out the other answer and put ‘infeasible’ next to it.

Methods to eliminating answers:

Method 1: Recommended

Cross out the infeasible answer, and put ‘infeasible’ next to it. You should put both answers initially.

e.g. x = 2, x = -7 infeasible

x = 2

Method 2:

Put the reason why a value is infeasible in the second last step, then write the answer.

e.g. x² = 36, x>0

x = 6

Method 1 is recommended, since you don’t have to list the reason, and it prevents the chance of giving the wrong reason.