Moderne Wiskunde 4 HAVO 4 Systematisch tellen
Voorkennis
Een boomdiagram
Een boomdiagram is een manier om alle mogelijkheden bij een telprobleem overzichtelijk weer te geven. Het laat zien om welke keuzes het gaat. Bij elk keuzemoment hoort een aantal takken en bij elke tak wordt de betreffende keuze genoteerd.
Elke route van het beginpunt naar een eindpunt is een mogelijkheid bij een telprobleem.
Voorbeelden

Begrippen
Boomdiagram
Takken
4.1 Mogelijkheden tellen
Regelmatige en onregelmatige boomdiagrammen
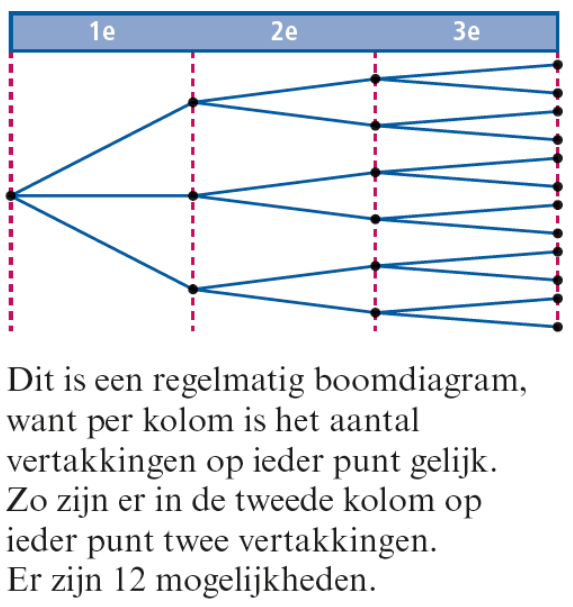
Bij het oplossen van een telprobleem is een boomdiagram vaak een handig hulpmiddel. In een boomdiagram geef je overzichtelijk weer welke mogelijkheden er zijn.
Als het aantal vertakkingen op elk punt in een kolom gelijk is, dan is het een regelmatig boomdiagram. Je kunt dan het aantal mogelijkheden uitrekenen zonder het hele boomdiagram te tekenen.
Als het aantal vertakkingen niet in elk punt in een kolom gelijk is, dan is het een onregelmatig boomdiagram. In dat geval moet je het hele boomdiagram tekenen of de mogelijkheden systematisch opschrijven.
Voorbeelden

Leerdoelen
Je leert wat regelmatige en onregelmatige boomdiagrammen zijn.
Begrippen
Onregelmatig boomdiagram
Regelmatig boomdiagram
4.2 Machtsbomen en faculteitsbomen
Een machtsboom
Een boomdiagram waarin bij elk keuzemoment het aantal takken gelijk is, noem je een machtsboom. Het aantal mogelijke volgorden is een macht.
Bij drie keuzemomenten met steeds vijf mogelijkheden is het aantal mogelijke volgorden gelijk aan 5*5*5=5³=125.
Voorbeelden

Een faculteitsboom
Een boomdiagram waarin bij elk keuzemoment het aantal takken één minder wordt, noem je een faculteitsboom.
Als je eerst drie keuzemogelijkheden hebt, daarna twee en tenslotte één, dan is het aantal mogelijke volgorden 3*2*1.
Een product zoals 12*11*10*…*3*2*1 heet een faculteit. Je noteert 12!.
Voorbeelden

Leerdoelen
Je leert hoe je met een machtsboom of een faculteitsboom het aantal mogelijkheden berekent.
Begrippen
Faculteit
Faculteitsboom
Machtsboom
4.3 Permutaties
Permutatie
Een ander woord voor volgorde of rangschikking is permutatie. Een permutatie van 3 uit 10 is een rangschikking van een rijtje van drie dat je kiest uit tien verschillende dingen: een eerste, een tweede en een derde. Een boomdiagram is een geschikt telmodel voor het aantal permutaties.
Het aantal permutaties van 3 uit 10 is 10*9*8=720.
Leerdoelen
Je leert hoe je het aantal permutaties berekent.
Begrippen
Permutatie
4.4 Routes in een rooster
Het aantal kortste routes in een rooster
Hoe bereken je het aantal kortste routes in een rooster?
Noteer bij elk punt dat maar op één manier is te bereiken het getal 1.
Stel voor elk ander punt vast wat de voorgangers zijn en tel de bijbehorende aantallen bij elkaar op.
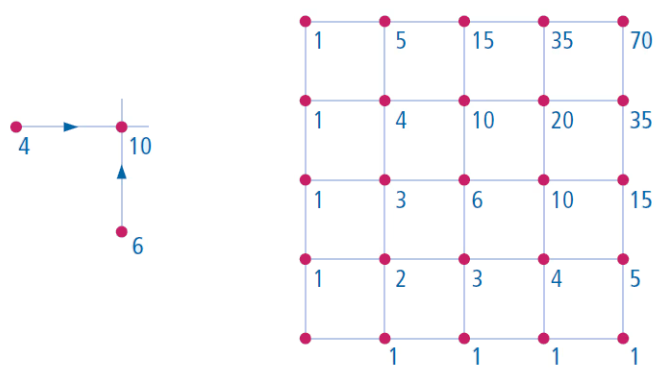
Voorbeelden
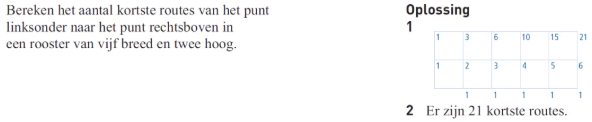
Rooster als telmodel
Bij telproblemen waarbij steeds gekozen moet worden uit twee mogelijkheden is een rooster een handig telmodel.
Leerdoelen
Je leert hoe je het aantal kortste routes in een rooster berekent.
4.5 Combinaties
Combinatie
Een ander woord voor een selectie is combinatie.
Een combinatie van 7 uit 10 is een selectie van zeven dingen uit tien verschillende dingen: zeven wel en drie niet.
Een rooster is een geschikt telmodel om het aantal mogelijke combinaties te berekenen, want zeven kiezen uit tien komt overeen met: op hoeveel manieren kun je in een rooster zeven stappen naar rechts en drie stappen omhoog doen.
Het aantal combinaties van zeven uit 10 noteer je als (10 7).
Dit spreek je uit als ’10 boven 7’.
Dit is het aantal kortste routes in een rooster van zeven breed en drie hoog. Je kunt dit ook met je rekenmachine uitrekenen.
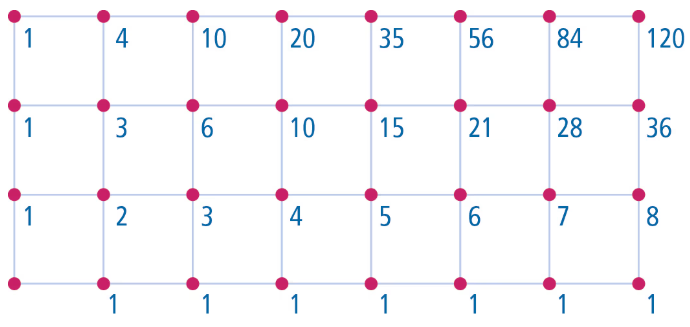
Voorbeelden

Leerdoelen
Je leert hoe je het aantal combinaties berekent.
Begrippen
Combinatie
4.6 Het goede telmodel kiezen
Een goed telmodel kiezen
Bij het oplossen van een telprobleem kies je een goed telmodel.
Ga na of je gebruik kunt maken van een boomdiagram, een rooster of een schema:
als je te maken hebt met de keuze uit twee mogelijkheden met vaste aantallen per mogelijkheid, dan is een rooster een handig telmodel;
heeft een boomdiagram een regelmatige structuur, dan kun je het aantal mogelijkheden berekenen door de aantallen vertakkingen per kolom met elkaar te vermenigvuldigen;
heeft het boomdiagram geen regelmatige structuur, dan moet je het boomdiagram tekenen of alle mogelijkheden systematisch opschrijven.
Voorbeelden



Resultaten van deelproblemen combineren
Er zijn telproblemen waarbij je het aantal mogelijkheden vindt door resultaten van deelproblemen te combineren.
Voorbeelden


Leerdoelen
Je leert hoe je bij een telprobleem een goed telmodel kiest.
Begrippen
Telmodel
Samenvatting leerdoelen | Extra oefening
Regelmatige en onregelmatige boomdiagrammen
Je weet wat regelmatige en onregelmatige boomdiagrammen zijn.
Bij het oplossen van een telprobleem is een boomdiagram vaak een handig hulpmiddel. In een boomdiagram geef je overzichtelijk weer welke mogelijkheden er zijn.
Als het aantal vertakkingen op elk punt in een kolom gelijk is, dan is het een regelmatig boomdiagram.
Je kunt dan het aantal mogelijkheden uitrekenen zonder het hele boomdiagram te tekenen.
Als het aantal vertakkingen niet op elk punt in een kolom gelijk is, dan is het een onregelmatig boomdiagram.
In dat geval moet je het hele boomdiagram tekenen of de mogelijkheden systematisch opschrijven.
Voorbeelden
Met een machtsboom of een faculteitsboom het aantal mogelijkheden berekenen
Je kunt met een machtsboom of een faculteitsboom het aantal mogelijkheden berekenen.
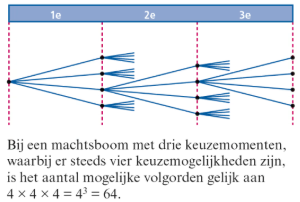
Een boomdiagram waarin bij elk keuzemoment het aantal takken gelijk is, noem je een machtsboom. Het aantal mogelijke volgorden is een macht.
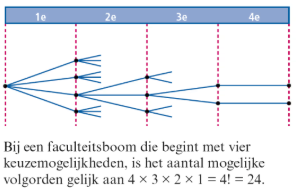
Een boomdiagram waarin bij elk keuzemoment het aantal takken één minder wordt en eindigt met één tak, noem je een faculteitsboom. Het aantal mogelijke volgorden is een faculteit. Een product van de vorm 8*7*6*…*2*1 heet 8 faculteit. Je noteert dit als 8!.
Voorbeelden
Het aantal permutaties berekenen
Je kunt het aantal permutaties berekenen.
Een ander woord voor volgorde of rangschikking is permutatie. Een permutatie van 6 uit 15 is een rangschikking van een rijtje van zes dat je kiest uit vijftien verschillende dingen: een eerste, een tweede tot en met een zesde.
Voorbeelden

Het aantal kortste routes in een rooster berekenen
Je kunt het aantal kortste routes in een rooster berekenen.
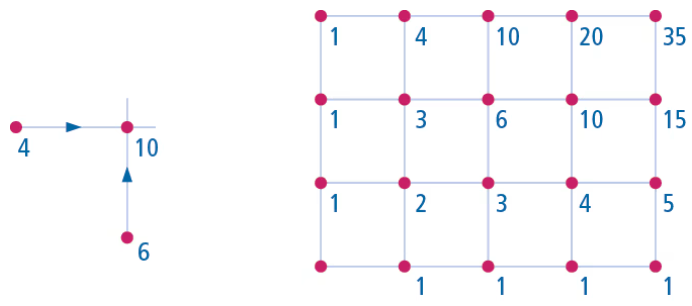
Noteer bij elk punt dat maar op één manier is te bereiken het getal 1.
Stel voor elk ander punt vast wat de voorgangers zijn en tel de bijbehorende aantallen bij elkaar op.
Voorbeelden

Het aantal combinaties berekenen
Je kunt het aantal combinaties berekenen.
Een ander woord voor een selectie is combinatie.
Een combinatie van 5 uit 12 is een selectie van vijf dingen uit twaalf verschillende dingen: vijf wel en zeven niet.
Een rooster is een geschikt telmodel om het aantal mogelijke combinaties te berekenen, want vijf kiezen uit twaalf komt overeen met: op hoeveel manieren kun je in een rooster vijf stappen naar rechts en zeven stappen omhoog doen.
Het aantal combinaties van 5 uit 12 noteer je als (12 5).
Dit spreek je uit als ’12 boven 5’.
Voorbeelden

Bij een telprobleem een goed telmodel kiezen
Je kunt bij een telprobleem een goed telmodel kiezen.
Bij het oplossen van een telprobleem kies je een goed telmodel. Ga na of je gebruik kunt maken van een boomdiagram, een rooster of een schema:
als je te maken hebt met de keuze uit twee mogelijkheden met vaste aantallen per mogelijkheid, dan is een rooster een handig telmodel;
heeft een boomdiagram een regelmatige structuur, dan kun je het aantal mogelijkheden berekenen door de aantallen vertakkingen per kolom met elkaar te vermenigvuldigen;
heeft het boomdiagram geen regelmatige structuur, dan moet je het boomdiagram tekenen of alle mogelijkheden systematisch opschrijven.
Voorbeelden

