Honors Geometry chapter 8

geometric mean - x² = ab; x = √ab

geometric mean (altitude) theorem [def] - the altitude drawn to the hypotenuse of a right triangle separates the hypotenuse into two segments. The length of this altitude is the geometric mean between the lengths of these two segments

geometric mean (altitude) theorem [equation] - segment 1 / altitude = altitude / segment 2

geometric mean (leg) theorem [def] - the altitude drawn to the hypotenuse of a right triangle separates the hypotenuse into two segments. The length of a leg of this triangle is the geometric mean between the length of the hypotenuse and the segment of the hypotenuse adjacent to that leg.

geometric mean (leg) theorem [equation] - hypotenuse / leg = leg / corresponding segment

pythagorean theorem (def) - the sums of the squares of the lengths of the legs of a right triangle is equal to the square of the length of its hypotenuse

pythagorean theorem (equation) - a² + b² = c²

pythagorean triple - three integers that follow the pattern of the pythagorean theorem

converse of the pythagorean theorem [def] - if the longest side squared is equal to the sum of the other sides squared in a triangle, then it is a right triangle

converse of the pythagorean theorem [equation] - c² = a² + b² = right triangle

pythagorean inequality theorem (acute) [def] - if the square of the length of the longest side of a triangle is less than the sum of the squares of the lengths of the other 2 sides, then the triangle is acute

pythagorean inequality theorem (acute) [equation] - c² < a² + b² = acute

pythagorean inequality theorem (obtuse) [def] - if the square of the length of the longest side of a triangle is greater than the sum of the squares of the lengths of the other two sides, then the triangle is obtuse

pythagorean inequality theorem (obtuse) [equation] - c² > a² + b² = obtuse

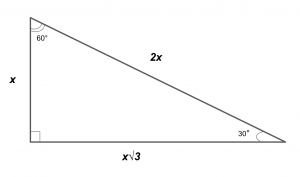
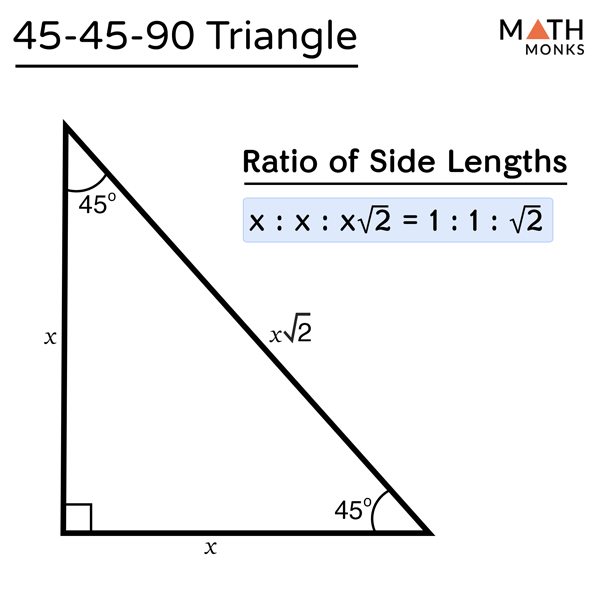
SOH-CAH-TOA - Sine: opposite/hypotenuse; Cosine: adjacent/hypotenuse; Tangent: opposite/adjacent

angle of elevation - angle made when you look up from the horizontal to the line of sight

angle of depression - angle made when you look down from the horizontal to the line of sight