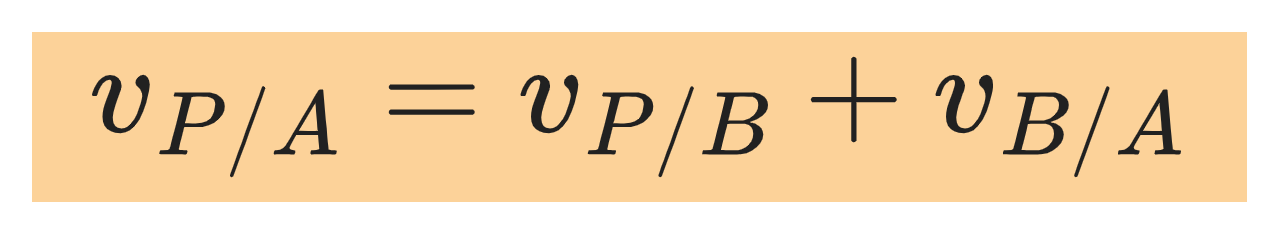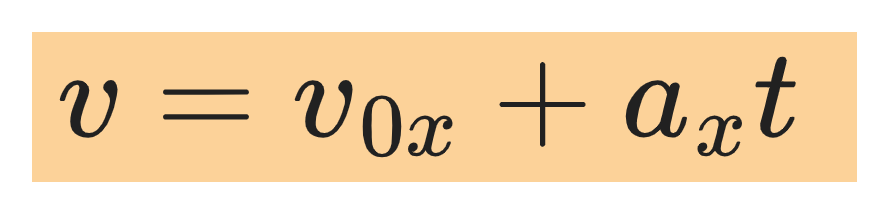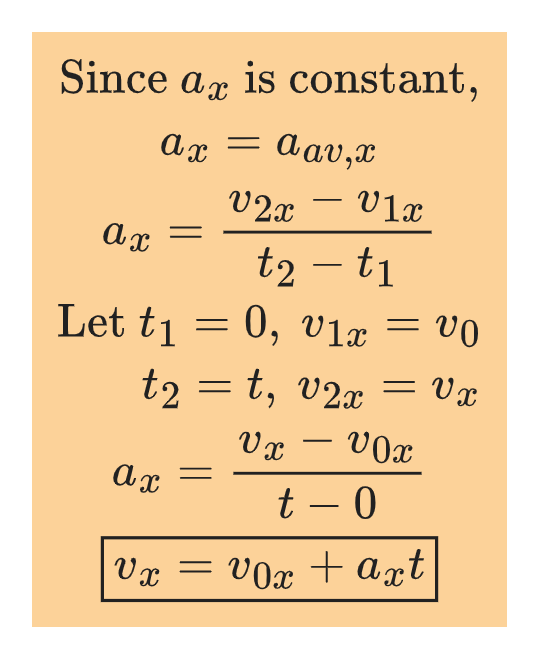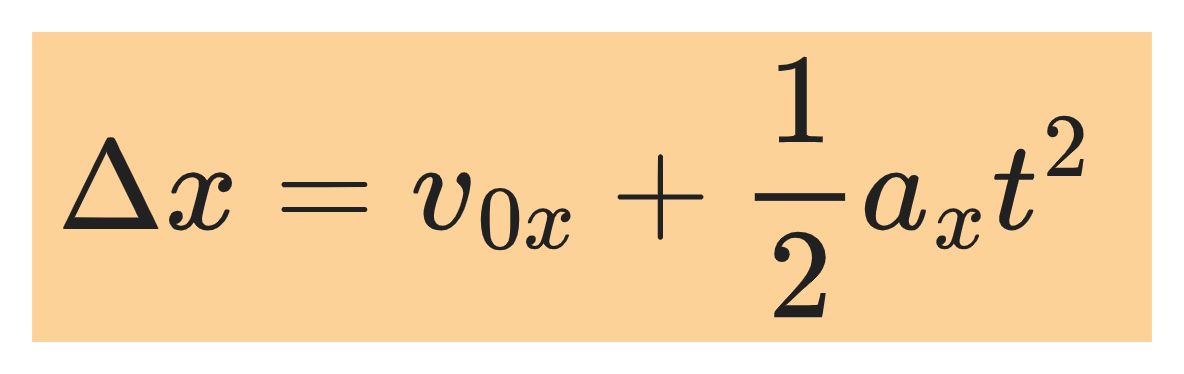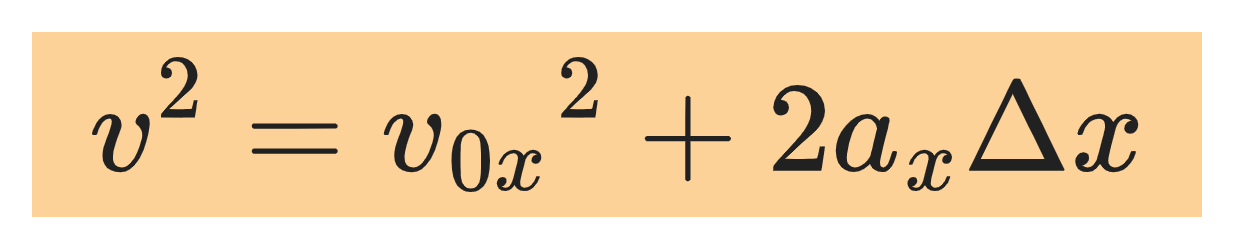Introduction

• Motion is a continuous change of position with time.

• Kinematics is the description of motion without regard to its causes. In this chapter, it is limited to motion along a straight line, called one dimensional motion.

3.1 Displacement and Average Velocity

• When an object moves along a straight line, we describe its position with respect to an origin O by means of a coordinate such as x. If the object starts at position x₁ at time t₁ and arrives at position x₂ at time t₂, the object’s displacement is a vector quantity whose x component is:

  

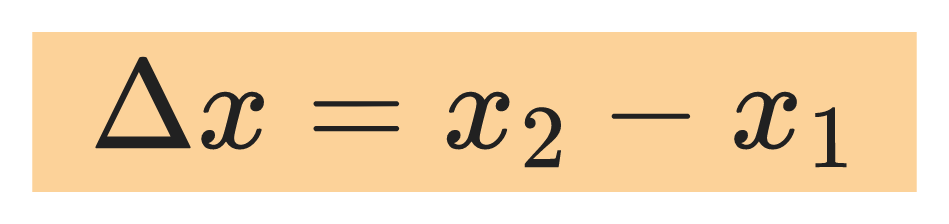
• Average velocity of the object during the interval (t₂-t₁) is defined to be a vector quantity whose x component is the change in displacement, Δx divided by the time interval, Δt

  Mathematically,

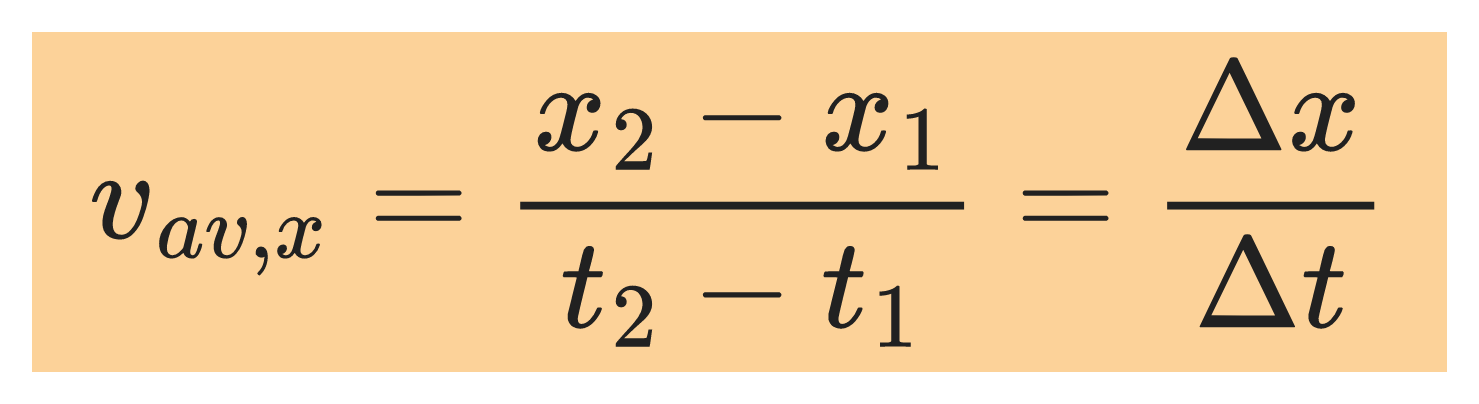
• NB: All other components of velocity vector are zero since motion is along one coordinate axis (x - coordinate in this case).

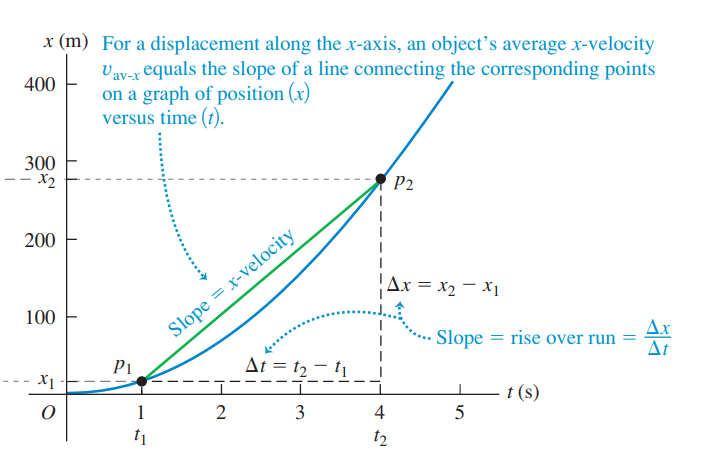
• The relationship between the position, x of an object and time t is often represented by a graph.

• The average velocity between two positions is the slope of a line connecting the two corresponding points on this graph of position as a function of time.

  

3.2 Instantaneous Velocity

• A particle’s velocity at any one specific instant of time or at one specific point in path is its instantaneous velocity.

• When average velocity is calculated for progressively smaller time intervals and thus shorter displacements, the average velocity approaches instantaneous velocity.

• Mathematically, the instantaneous velocity is called the limit of average velocity as the time interval approaches zero.

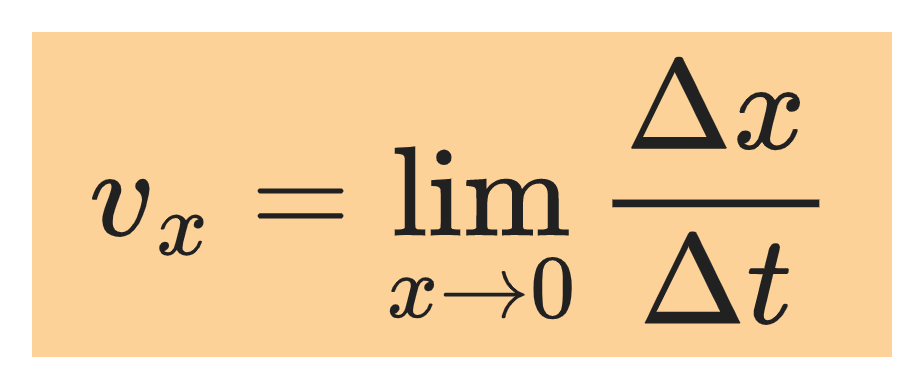
• On a graph of a coordinate x as a function of time, the instantaneous velocity at any point is equal to the tangent line to the curve at that point.

• NB: The term velocity usually refers to instantaneous velocity rather than average velocity. The sign of a velocity component always depends on the choice of coordinate system, including the location of the origin and the choice of positive axis direction.

Significance of the sign of velocity

• The sign of a velocity component always depends on the choice of coordinate system, including the location of the origin and the choice of positive axis directions.

• x tells us where the particle is, and vₓ tells us how it is moving.

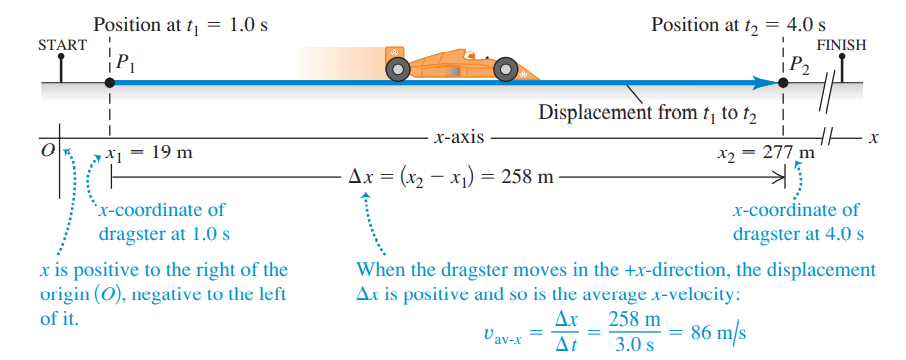
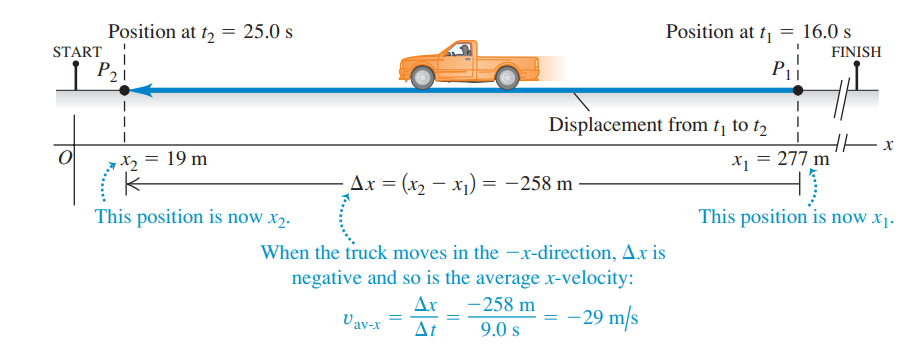
• It’s not necessarily the case that positive velocity means motion to the right and negative velocity means motion to the left because the choice of positive axis direction as well as the choice of coordinate system and location of the origin is arbitrary.

Rules for the sign of velocity

NB: The location of the origin determines whether x is getting more positive or negative.

3.3 Average and Instantaneous Acceleration

• Acceleration describes the rate of change of velocity with time.

• Like velocity, acceleration is a vector quantity. In straight line motion its only non-zero component is along the coordinate axis (x or y).

• Average acceleration of an object as it moves from x₁ (at time t₁) to x₂ (at time t₂) is a vector quantity whose x component is the change in the x component of velocity, Δvₓ=v₂-v₁ divided by the time interval Δt=t₂-t₁

• Mathematically,

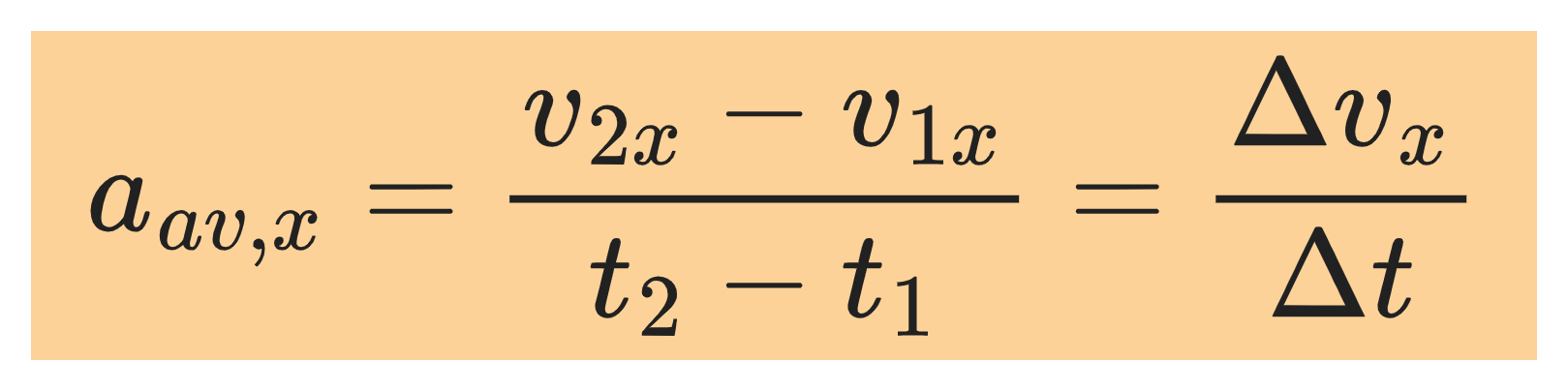
• Unit: m/s² (meters per second squared)

Instantaneous Acceleration

• To define instantaneous acceleration at point x₁ (shown above) we take the second point x₂ to be closer and closer to first point x₁ so that the average acceleration is calculated over progressively shorter and shorter time intervals.

• The x component of instantaneous acceleration is defined as the limit of Δvₓ/Δt as Δt approaches zero:

  

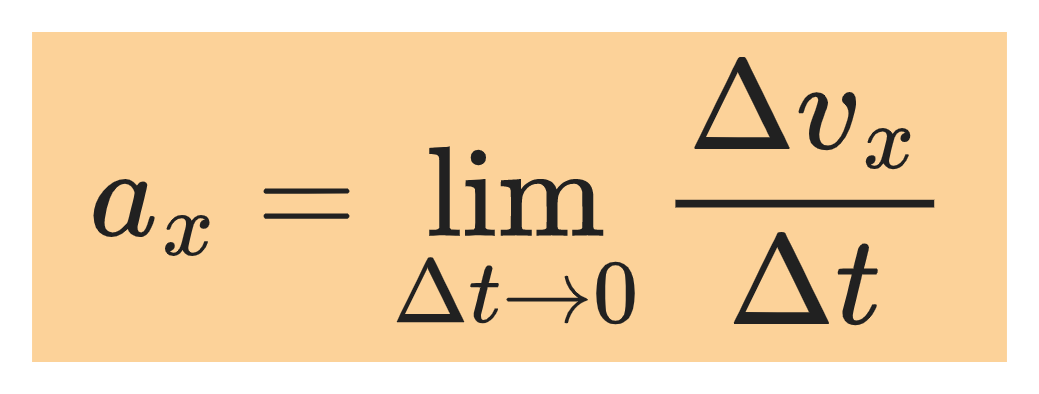
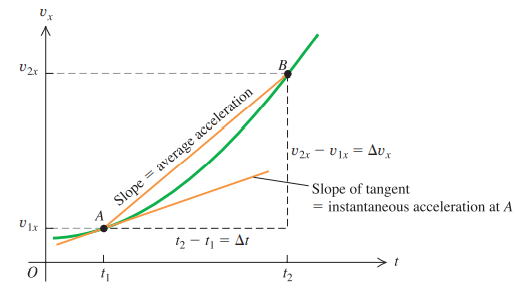
• On a graph of vₓ versus t, average acceleration between two points is the slope of the line connecting the two corresponding points.

• The slope of the tangent line to a curve at a point is the instantaneous acceleration at that point.

Significance of sign of acceleration

• 

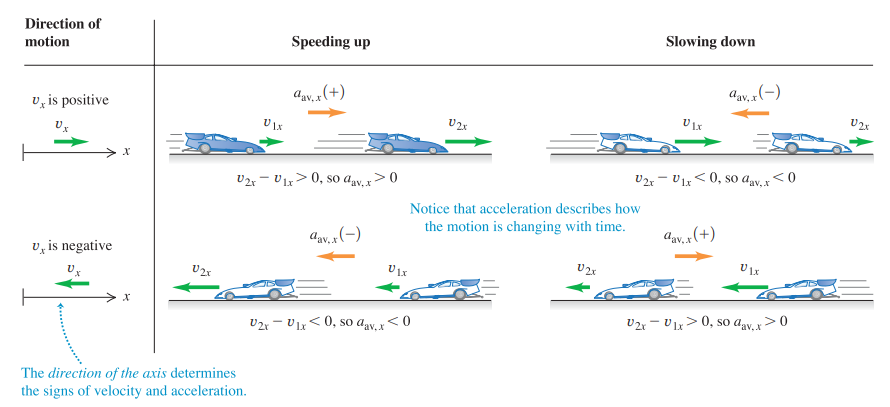
• The algebraic sign of the acceleration does not tell you whether a body is speeding up or slowing down. You must compare the signs of the velocity and the acceleration.

Rules for the sign of acceleration

Acceleration and the Human Body

• Acceleration requires a force and so an object subjected to very a high acceleration and its associated force may suffer damage.

• The earth’s gravitational attraction causes objects to fall with a downward acceleration with a magnitude of about 9.8m/s², denoted by g. The human body can withstand accelerations on the order of g without damage.

3.4 Motion with constant acceleration

• A particle moves with a constant acceleration if its velocity changes by equal amounts in equal time intervals.

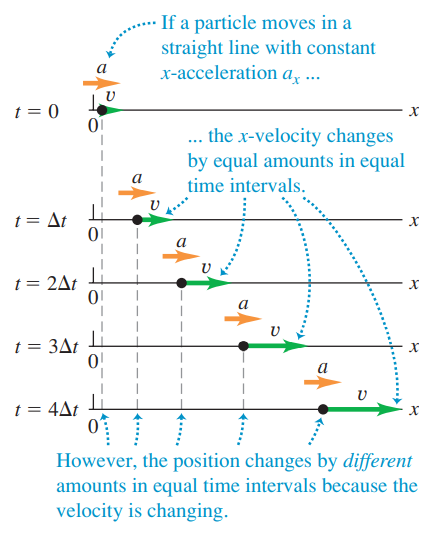
• A graph of vₓ versus t has a constant slope because the acceleration is constant. The graph of aₓ versus t is a horizontal line since acceleration is constant.

Equations of Motion for Constant Acceleration

3.5 Proportional Reasoning

• Proportional reasoning is an analytical technique that can be used to describe general relationships between variables without reference to specific details of numerical values.

• If we have two variables x and y, the relationship between them could be one of the following forms:

  y = kx

  y = kx²

  y = k/x

  y = k/x²

• Proportional reasoning seeks to among other things, determine what form the relation between the two variables takes.

3.6 Freely Falling Objects

• Objects in free fall move under the influence of gravity alone.

• The term free fall includes objects that are initially at rest as well as objects with an initial velocity.

• Free fall is a form of idealized motion. When the effects of air resistance are ignored, all bodies at a particular location fall with the same acceleration, regardless of size or weight.

• The constant acceleration of freely falling objects is called acceleration due to gravity, g. At or near the earth’s surface the magnitude of g is approximately 9.8m/s².

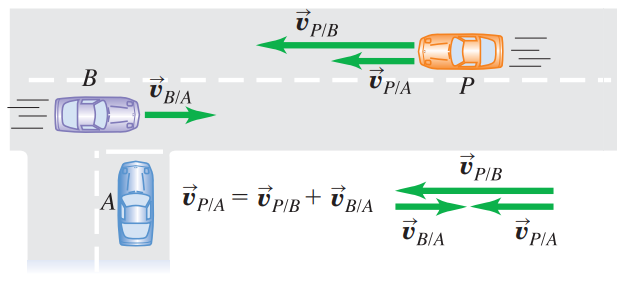
3.7 Relative Velocity along a Straight Line

• When two moving observers measure the velocity of a moving body, they get different results if one observer is moving relative to the other. The velocity seen by a particular observer is called the velocity relative to that observer, or simply relative velocity.

• When an object P moves relative to an object (or reference frame) B, and B moves relative to a second reference frame A, we denote the velocity of P relative to B by:

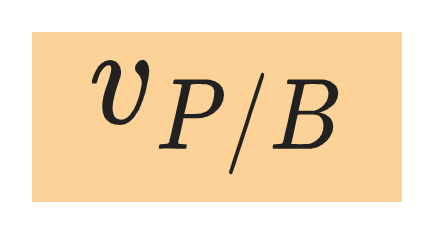
the velocity of P relative to A by:

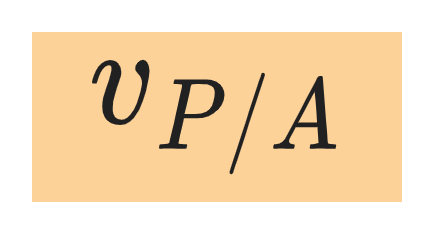
and the velocity of B relative to A by

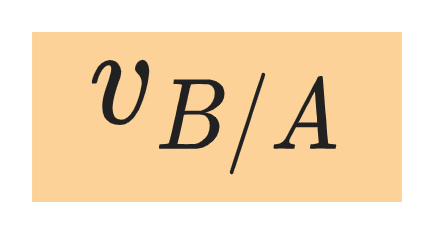
• These velocities are related by: