1. Pressure

• Pressure (P):

  ​

  Where:
  F= Force, A = Area

• Pressure due to a fluid column:

  P=hρg

  Where:
  h = height of the fluid,
  ρ = density of the fluid,
  g = acceleration due to gravity

2. Pascal's Law

• Statement:
  "Pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the container."

• Applications:

  • Hydraulic lift:

    

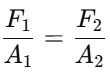
  • Where

  • F1,F2 are forces, and

  • A1​,A2​ are areas.

3. Viscosity

• Newton's Law of Viscosity:

  η=(F*L)/(A*V)

  Where:
  η = coefficient of viscosity,
  A = area,
  F = force required to maintain the flow (N)

• V/L​ = velocity gradient (rate of change of velocity with distance)

• Stokes’ Law:

  F=6πηrv

  Where:
  r = radius of the sphere,
  v = velocity of the object

• Terminal Velocity:

  vt=2r2(ρs−ρf)g9ηv_t = \frac{2 r^2 (\rho_s - \rho_f) g}{9 \eta}vt​=9η2r2(ρs​−ρf​)g​

  Where
  ρs\rho_sρs​ = density of the sphere,
  ρf\rho_fρf​ = density of the fluid

4. Streamline and Turbulent Flow

• Equation of Continuity (Conservation of Mass):

• A1v1=A2v2

• Where

• A = cross-sectional area,

• v= velocity

5. Bernoulli’s Theorem

• Energy Conservation for Fluids:

  P+(1/2)ρv^2+ρgh=constant

  Where:
  P = pressure energy,
  (1/2)ρv^2 = kinetic energy per unit volume,
  ρgh = potential energy per unit volume

6. Surface Tension

• Surface Energy:

  Surface Energy=TΔA

  Where T = surface tension,

• ΔA = change in surface area

• Excess Pressure:

  • Inside a liquid drop: ΔP=2T/r

  • Inside a bubble: ΔP=4T/r

• Capillary Rise:

  h=2Tcos⁡θ/ρgrh

  Where:
  θ = angle of contact,
  r = radius of the capillary

Simplified Notes:

1. Viscosity:
   It’s the measure of a fluid's resistance to flow. Honey has higher viscosity than water.

2. Bernoulli's Principle:
   Faster-moving fluids exert lower pressure (used in airplanes and chimneys).

3. Surface Tension:
   It’s the tendency of liquid surfaces to shrink into the minimum surface area (seen in soap bubbles and water droplets).

4. Capillarity:
   Liquids rise or fall in a capillary tube due to adhesion and cohesion.

5. Streamline vs. Turbulent Flow:

   • Streamline: Smooth and regular flow of fluid.

   • Turbulent: Chaotic and irregular flow.