Chapter 1 - The Properties of Gases
- Gas - A collection of molecules/atoms in continuous random motion with an average speed that increases with temperature raise.
- It fills any container it occupies
- Simplest state of matter
1.1 The states of gases
- The physical state (physical condition) of a substance depends on its physical properties.
- The state of a pure gas is specified by its volume (V), number of moles (n), pressure (P), and temperature (T). However, we only need three variables since the fourth has a fixed value. This is described by an equation of state.
- Equation of state → p = f(T,V,n)
- It tells us that if we know the values of T, V, and n, the pressure has a fixed value.
Equation of state of a perfect gas
- p = nRT/V
- R is constant.
Pressure units
| [[Name[[ | [[Symbol[[ | [[Value[[ |
|---|---|---|
| pascal | 1 Pa | 1 N m^-21 kg.m^-1.s^-1 |
| bar | 1 bar | 10^5 Pa |
| atmosphere | 1 atm | 101.325 Pa |
| torr | 1 Torr | 133.32… Pa |
| millimeters of mercury | 1 mmHg | 133.322… Pa |
| pound per square inch | 1 psi | 6.894757… kPa |
Pressure
Pressure - Force divided by the area where the force was applied.
- SI unit of pressure → Pascal (Pa)
- Most common units for pressure - Pascal, atmosphere, and bar.
- A pressure of 1 bar is the standard pressure for reporting data.
Mechanical equilibrium → A condition of equality of pressure on either side of a movable wall.
- ^^Ex. →^^ If two gases are in separate containers that share a movable wall, the gas that has the higher pressure will tend to reduce the volume of the gas that has lower pressure. After a while, the two pressures will be the same meaning there’s no more movement.
Barometer - Used to measure the pressure done by the atmosphere.
Pressure gauge - Used to measure the pressure of a gas inside a container.
Temperature
Temperature - The property that indicates the direction of the flow of energy through a thermally conducting, rigid wall.
There are two types of boundaries that can separate the objects.
- Diathermic boundary → If there’s a change when two objects with different temperatures come together. Diathermic means thermally conducting. A metal container has diathermic walls.
- Adiabatic boundary → If there’s no change even when two objects with different temperatures come together. Adiabatic means thermally insulating. A vacuum flask is an adiabatic container.
Thermal equilibrium → When there’s no change of state if two objects are in contact through a diathermic boundary.
Zeroth Law of Thermodynamics → If object A is in thermal equilibrium with B and B is in thermal equilibrium with C, then C is in thermal equilibrium with A. This justifies the concept of temperature and the use of thermometers.
Measures of temperature - Celcius, Fahrenheit, or Kelvin,
- Kelvin is the one used in thermodynamics.
- To convert from Celcius to Kelvin, we use the following formula:
K = °C + 273.15
1.2 The gas laws
The perfect gas law
Boyle’s and Charle’s Laws are limiting laws, meaning they are only true to a certain limit.
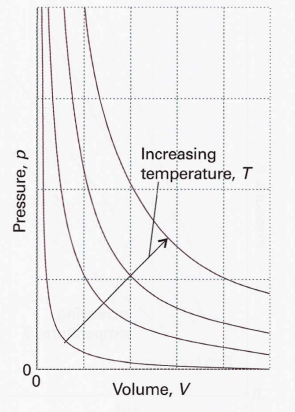
According to Boyle’s Law, isotherms of gases are hyperbolas.
Perfect gas equation → pV = nRT
R - Constant of proportionality, gas constant.

Perfect or ideal gas - A gas that obeys this equation exactly under all conditions.
Molecular interpretation 1.1 - The kinetic model of gases
Molecular explanation of Boyle's law →If a sample of gas is compressed to half its volume, then twice as many molecules strike the walls in a given period of time than before it was compressed. Therefore, the average force applied on the walls is doubled.
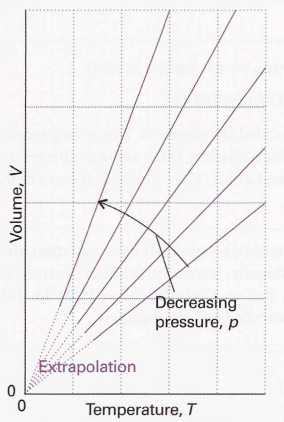
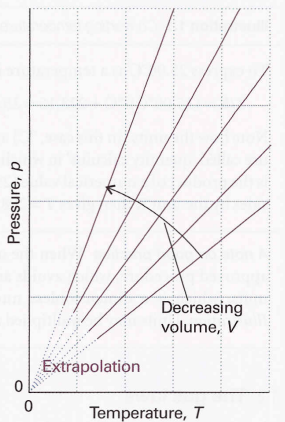
Molecular explanation of Charles's law → Raising the temperature of a gas increases the average speed of its molecules. The molecules collide with the walls more frequently and with greater impact. So they apply greater pressure on the walls of the container.
The kinetic model is based on three assumptions:
- The gas consists of molecules of mass in a non-stop random motion.
- The size of the molecules is insignificant, in the sense that their diameters are much smaller than the average distance traveled between collisions.
- The molecules interact only through brief, infrequent, and elastic collisions.
Elastic collision → Collision in which the total translational kinetic energy of the molecules is conserved.
STAP → Standard ambient temperature and pressure, which is 298.15 K and 1 bar. The molar volume of a perfect gas at STAP is 24.789 dm^3 mol^-1.
STP → Standard temperature and pressure, which is 0°C and 1 atm. The molar volume of a perfect gas at STP is 22.414 dm^3 mol^-1.
Molar volume formula - Vm = RT/p
Mixture of gases
Partial pressure, pp, of a gas J in a mixture:
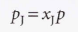
Dalton’s Law → When all the gases are perfect, the partial pressure is the pressure each gas would occupy if it occupied the same container alone at the same temperature.
Real gases
1.3 Molecular interactions
Repulsive forces - Contribute to expansion. They are significant only when molecules are almost in contact.
Attractive forces - Contribute to compression. They have a long range, but they’re only important when the molecules are fairly close together.
Intermolecular forces - They are important at low temperatures since molecules travel slowly meaning they can be captured by one another.
- They are insignificant at low pressures.
- At moderate pressures, the attractive forces dominate the repulsive forces making the gas more compressible.
- At high pressures, the repulsive forces dominate the attractive forces making the gas less compressible.
Compression factor (Z) - The ratio of its measured molar volume to the molar volume of a perfect gas at the same pressure and temperature.
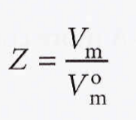
We can also use this formula:
![]()
Virial coefficients
Virial equation of state
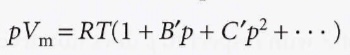
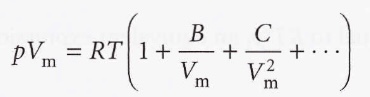
The terms in parentheses can be identified with the compression factor, Z.
The coefficients B, C, etc. are the second, third, … virial coefficients. The first virial coefficient is 1. The third virial coefficient is usually less important than the second coefficient since at typical molar volumes, C/Vm ^2 << B/Vm.
Boyle temperature - The temperature where Z → 1 with zero slope at low pressure or high molar volume. It’s where the properties of the real gas coincide with the ones of a perfect gas at p → 0.
Condensation
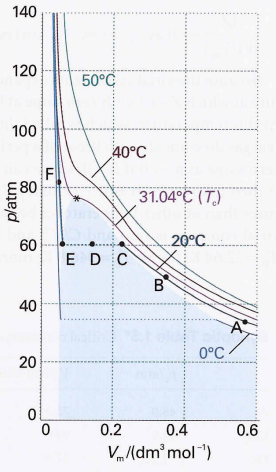
- Vapor pressure → Pressure corresponding to CDE, when both liquid and vapor are present in equilibrium.
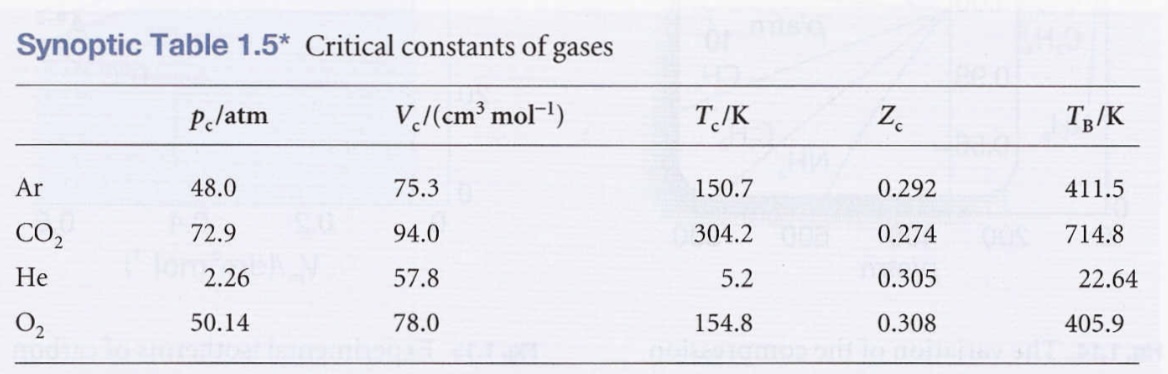
Critical constants
- Critical point →The point where a surface separating two phases doesn’t appear and the volumes at each end of the horizontal part of the isotherm merge to a single point.
- Critical temperature (Tc) - The temperature at the critical point.
- Critical pressure (Pc) - The pressure at the critical point.
- Critical molar volume (Vc) - The volume at the critical point.
1.4 The van der Waals equation
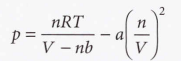
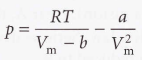
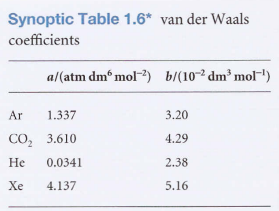
Van der Waals coefficients - The constants a and b. They are characteristic of each gas, not related to temperature:
Features of the equation
- Perfect gas isotherms - Obtained at high temperatures and large molar volumes.
- Liquids and gases coexist when cohesive and dispersing effects are in balance.
- The critical constants are related to the van der Waals coefficients.
1.5 The principle of corresponding states
- Principle of corresponding states - The observation that real gases at the same reduced volume and reduced temperature exert the same reduced pressure.