Algorithms: The Building Blocks of Programming

Algorithms

• An algorithm is a set of steps to do a task.

• Recipes are algorithms.

  • They are a set of steps to prepare food.

• Instructions for taking medicine make up an algorithm.

• Directions to get from one location to another are an algorithm.

• In computer science, algorithms are the set of steps to solve a problem or complete a task.

• Algorithms are implemented with software.

• Examples are programs to:

  • Calculate grade averages

  • Run the air conditioner when the room temperature reaches 78°F

  • Calculate the shortest route from home to school on your GPS

• Algorithms have the potential to solve many problems once the programs are written for them to run.

• A section of code may work independently or can be used with other programming modules.

  • These program modules read in values, make computations as needed, and produce output to automate processes.

Languages for Algorithms

• Algorithms can be written in several ways. Natural language is our native speaking and writing language, so it is much easier for people to use and understand.

• Programming languages are very strict with their syntax, which is like their grammar and structure.

• Pseudocode is used to map out a program’s structure before beginning to write the code and uses a combination of natural and programming languages.

  • Pseudocode cannot run on computers and needs to be translated to a programming language to do so.

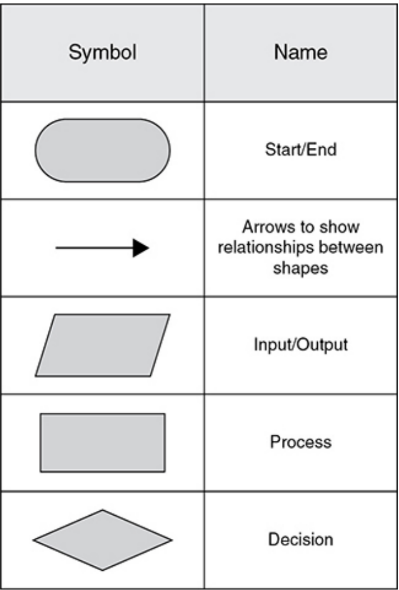
Flowcharts

• Flowcharting helps to visualize how the program will be structured. You may see places for loops and procedures at this early stage.

• There are predefined shapes used by programmers for creating flowcharts.

• While there are many shapes, the basics are as shown in the following chart.

• Many software programs, including word processing software, include flowcharting shapes.

Algorithm Readability and Clarity

• Clarity refers to how easy it is to understand.

  • Generally, a program that is readable is clear.

• Readability is important to help programmers understand a program.

  • The original programmer may not be the person who makes changes to it later.

• Features of readability and clarity include variables and procedures that are named according to their use and effective documentation of the program with comments in the code along with blank lines to separate sections of code.

Foundations of Computer Programming

Variables

• Variables are placeholders for values a program needs to use.

• A program may need variables for numbers, both integers and real numbers, as well as text fields and Boolean values.

• Variables can be used in expressions, both mathematical and textual.

• An important aspect of variables is naming them well.

• Variables are data abstractions because we do not need to know the details of how and where the values are stored in memory.

Data Types

• Data types are the way computers assign some meaning to these binary digits.

• Doing this allows us to use those values in particular ways, such as numbers and text.

• There are four main data types you should understand for the exam: strings, integers, real (fractional) numbers, and Booleans.

Strings

• Strings are text fields that are just a series of characters and are denoted with quotation marks around the string field.

• Any character, number, or symbol can be part of a string.

• When numbers are part of a string, then they will be considered to be text, like in a street address.

  • In this case, you cannot use them in calculations because they are text fields, not numbers.

Integers

• Integers are whole numbers. (They do not have a decimal point.)

• Integers can be used in mathematical operations and expressions, whereas strings (text fields) cannot.

“Fractional” Numbers

• These are numbers with a decimal point, even if a number has 0 (zero) for the decimal value, such as 52.0.

• These numbers can also be used in mathematical operations and expressions.

Mathematical Processes

• Most programming languages include mathematical operations.

• • Add

• • Subtract

• * Multiply

• / Divide

• Modulus math uses division but only provides the remainder as the answer, not the quotient.

• MOD is the symbol used for modulus math in many programming languages.

• For example:

  • 20 MOD 4 = 0 The quotient is 5 with a remainder of 0, so the answer is 0

• A common use for “MOD math” in programming is to find even or odd numbers.

  • A number that is divisible by 2 with a remainder of 0 is even.

Assignment Statements

• To assign a value to a variable, the assignment operator is used.

• In many programming languages, a single equals sign, =, is used as the assignment operator.

• The variable name is always on the left of the ← sign.

• The programming language will evaluate the right hand side of the assignment operator and then place the value into the variable on the left-hand side of it.

• The previous value stored in a variable is overwritten by a new assignment statement.

  • In this example, a variable named score is assigned the value 10.

  • It is then assigned the value 11.

  • The value 10 is gone and no longer available.

• Expressions are calculations to be evaluated to an answer or single value.

• In computer science, the value is then assigned to a variable if the value will be needed later.

• It also could be displayed on a screen or printed.

• You will get an error if you write:

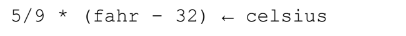
• The variable must be on the left and the assignment arrow points left.

• The expression will be evaluated and loaded into the variable celsius.

• P Parentheses

• E Exponents

• M Multiplication

• D Division

• A Addition

• S Subtraction

Boolean Values

• Boolean values are one of the foundations of computer code.

• Understanding Boolean is important for writing correct, readable, and efficient code.

• Boolean values can only be true or false, needing only one bit to represent its value.

• Relational operators are used with Boolean values.

• These are just like in your math class:

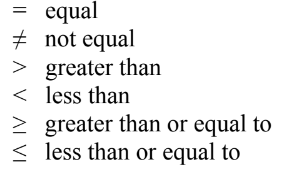
Compound Conditional Statements Using Logical Operators: AND, OR, NOT

• Boolean expressions can be simple or compound.

• Multiple expressions can be combined using the logical operators AND, OR, and NOT.

• These also evaluate to either true or false.

AND LOGICAL OPERATOR

• To be true, both of the operands on either side of the AND operator must be true when evaluated individually.

• In the example below, “licenseEligible” will be set to true only when the age is greater than or equal to 16 and the Boolean variable “learnersPermit” is true.

• Otherwise, “licenseEligible” will be set to false.

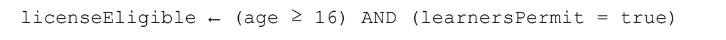
OR LOGICAL OPERATOR

• For the OR operator, either or both of the operands can be true for the condition to be true.

• In this example, if the day is a Saturday OR the month is July, then the sleepLate variable will be true.

• The day can be any day as long as the month is July, and the month can be any month as long as the day is Saturday for sleepLate to be true.

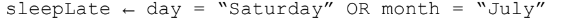
NOT LOGICAL OPERATOR

• With the NOT operator, if a condition was true, then NOT makes it false.

• If a condition was false, then NOT makes it true.

Program Statements

• All programs can be written using a combination of only three types of statements.

• These statements are used over and over and can be combined for more complex needs, but there are only three.

Sequential

• These are statements that are executed as written in order in the program.

• As we start writing our programs, a code statement has an action that will be executed when the program is run.

• Once a statement is complete, the next statement is run.

• Naturally, they have to be in the correct order to accurately complete the algorithm.

Selection Statements

• These are a key component to many programs.

• They use the “if (condition)” structure, and the evaluation of the condition uses Boolean values.

• As we know, Booleans can only be either true or false, so the program statements associated with the condition only run when the condition at that moment evaluates to “true.”

• This changes the flow of the program from every statement running sequentially to filtering out some of the code that will execute, based on the Boolean value.

• Notice that the code to be executed when the condition is true is surrounded by the curly braces, { }, in the “Text” version.

• The code within the braces is indented, which helps with readability.

• It also makes it easier to see if you are missing a closing brace }!

Iterative

• Iterative statements are also referred to as repetitive statements or loops.

• This type of programming statement also changes the sequence of lines of code that are executed.

• Code that is associated with these statements repeats as many times as specified before continuing with the rest of the program.

REPEAT n TIMES Loop

• This loop will repeat a specified number of times: “n” is a variable that must be set to a positive integer for the loop to run.

• The code that is repeated is indented underneath the REPEAT statement and within the braces, { }, just like with the IF/ELSE statements.

• The braces, { }, are required for loops in this course.

• The indentation is good programming practice.

REPEAT UNTIL (Condition) Loop

• The REPEAT UNTIL loop has a condition to evaluate at each iteration of the loop.

• The loop will continue to run while the condition evaluates to “false.”

• This is similar to how an IF statement works except the condition for the IF statement must evaluate to true for it’s code to execute.

• Combining Algorithms: One of the key features of algorithms is that once they are created, you can use them over and over, combine them for more complex problem solving, or modify them for a new use.

Common Algorithms

• Determining the maximum or minimum number from two or more numbers.

• The pseudocode for the maximum of two numbers is:

  • Compare the numbers.

  • Store the larger number as the maximum.

• For the minimum of two numbers:

  • Compare the numbers.

  • Store the smaller number as the minimum.

• If you have more than two numbers, a computer can still only compare two at a time.

• One number would be the current largest (or smallest), and the other would be the next number to compare it to.

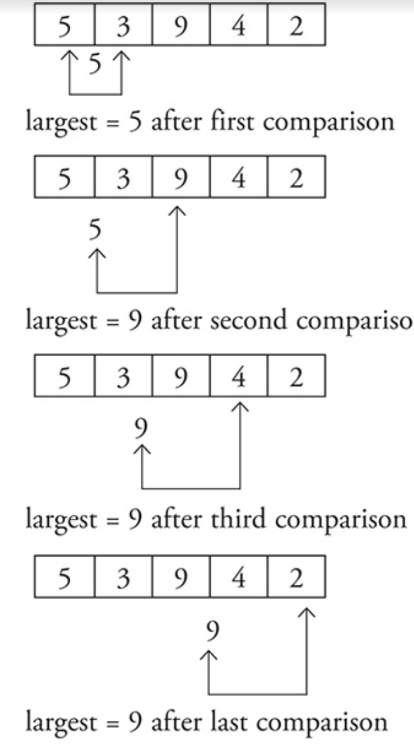
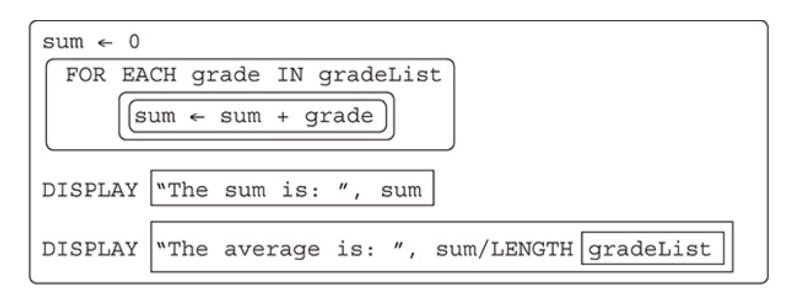
• Another common algorithm is calculating the sum and average of a group of numbers.

• This is fairly straightforward since it is a concept you have already learned in math class.

• One key element to remember is that you need to keep count of how many numbers you have added together so you will be able to calculate the average.

Robots

• There are four commands you are responsible for understanding and using.

• The triangle represents the robot’s starting point and the direction it is facing.

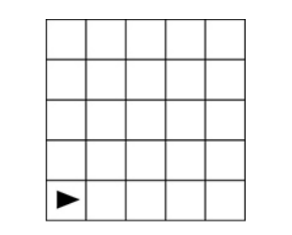
• One command the robot can follow is MOVE_FORWARD.

• The robot moves one step forward in the direction it is already facing.

• If the command would place the robot in a blacked-out box or past the border of the maze, the command cannot be executed.

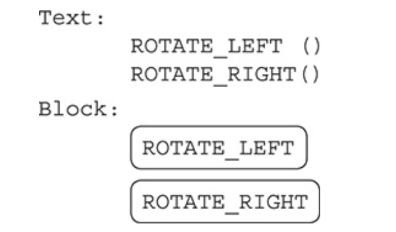
• The robot can also rotate left or right.

• The robot only changes the direction in the square it is already in.

• It does NOT move forward.

• Finally, there is a command, CAN_MOVE, that we can use to determine if the robot can make a valid move forward before moving.

• It returns a Boolean value, true or false.

• The mazes often have boxes blacked out.

• This means that the robot cannot land on or pass through those.

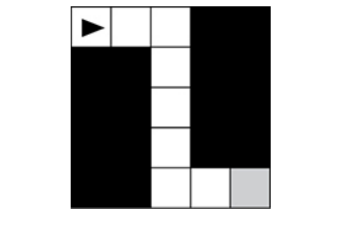
• CAN_MOVE can be used in an IF statement in your code to navigate through the maze.

  • This command takes a parameter that indicates the direction to test.

Lists

• Lists are a collection of items, such as a grocery list or a playlist of music.

• A list in a program can be a collection of numbers, words, phrases, or a combination of these.

• Usually a list only contains one type of data in a single list, but some programming languages do allow different types of data in the same list.

• Lists provide the ability to store more than one value in the same variable, separated by commas, when the variable is defined as a list.

• Lists are also called arrays in some programming languages.

List Indices

• Individual items in a list are called elements and are accessed by position using an index.

• Index positions are always integers and are enclosed within square brackets [index].

Built-in Methods

• Most programming languages will have built-in procedures, or “methods,” of common functionality to use with lists.

• Adding an item to a specific position in a list.

• The INSERT command causes elements to the right of the indicated index position, i, to shift right one position to make room for the new element.

• Appending an item to the end of the list.

• The APPEND command will add the new element to the end of the list, so no index position is needed.

• The size of the list increases by one.

• Removing an item from a list.

• The REMOVE command deletes the element at the provided index position and shifts the remaining elements one position to the left.

• The size of the list decreases by one.

• Length. The length of a list is the number of elements in the list.

Checking Each Item in a List

• The above statement is a loop that will automatically repeat the code for each element in the list.

  • This is called traversing a list.

• The programmer chooses the name for the iteration variable “item”.

• Each pass of the loop will assign the value of the next element in the list to the variable “item”.

• Processing lists with a FOR EACH loop takes advantage of features of both structures.

Common Algorithms

• There are algorithms that are frequently needed for processing lists with iteration.

• These include finding the largest or smallest number in a list.

• Here is an example using a REPEAT UNTIL loop with a list of grades.

• Another common algorithm is finding the sum and average of the values in a list.

Searching

• Searching deals with finding the needed element from everything in the dataset or determining that it is not there.

• LINEAR SEARCH: Linear searches, also called sequential searches, check each individual record, starting at the beginning and going to the end, one after the other in order to either find the desired data or to determine it is not in the dataset.

• BINARY SEARCH: Binary searches are far more efficient than linear searches.

  • However, data must be sorted to use a binary search.

  • The binary search is considered a “divide and conquer” algorithm because it divides the dataset into two equal parts.

Procedures

• Procedures are also called functions in some programming languages.

• These are sections of code that will be executed only when they are called by the main program or another procedure.

• They must be defined in a program before they can be used in the program.

Parameters/Arguments

• The use of parameters can make procedures more flexible.

• Parameters allow the calling program to send values to the procedure.

• They are passed to the procedure as arguments when the procedure is called.

• The values sent to the procedure can be different each time, making the procedure more flexible through the ability for multiple calls to the same section of code.

Calling a Procedure

• When the procedure is “called,” the program will pause at that location and execute the code in the procedure.

• When the procedure finishes, control returns back to the line of code where the call occurred.

• This is another programming structure that modifies the sequential flow of the program.

• Procedural abstraction: You only need to know the name of the procedure, the number and type of parameters, and the output to expect.

Return

• Procedures have an optional feature called a return statement.

• The return statement has two uses.

• One purpose is to end a procedure before the end of the code is reached.

• No other code in the procedure will be executed after the return statement.

• The other use is to send a value back to the calling program.

• Built-in Procedures: Built-in procedures are prewritten and tested code that are included with the programming language.

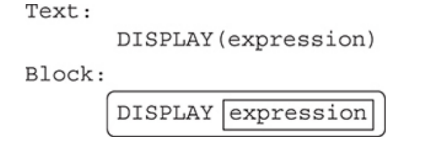
• DISPLAY(): DISPLAY() is a built-in procedure used for this course on the exam.

  • We do not know how this procedure is coded, only that we can use it multiple times, pass it different types and values to print, and that it works.

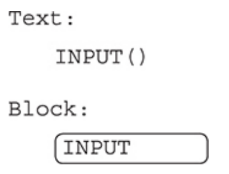
• INPUT(): It accepts data from the user, usually from the keyboard.

  • When the programming language sees this command, it will pause the program and wait for something to be typed on the keyboard.

APIs AND “LIBRARIES”

• For each programming language, there are prewritten programs to provide commonly needed functionality, and these programs are stored in libraries, which are folders with several programs.

• API stands for “Application Programming Interface.”

• The API documentation provides the information needed to set up the interface and use the newly connected software.

RANDOM

• Generating random numbers is a frequently needed feature in programs.

• Most programming languages have a library of prewritten code for a variety of random number generators.

• RANDOM needs two values passed to it using arguments, the beginning and ending range for the selected random number.

• Simulations: Simulations are designed to represent and mirror the real world for testing.

Analyzing Algorithms

• An instance of a problem is a specific example.

• A decision problem has a yes or no answer.

• An optimization problem is one that should find the best solution for the problem.

Algorithm Efficiency

• The efficiency of algorithms deals with resources needed to run it in terms of how long it will take and how much memory will be needed.

• This becomes especially important with extremely large datasets, and efficiency is usually stated in terms of the size of the input.

• Efficiency can be determined by mathematically proving it and informally measured by actually running it on datasets of different sizes and measuring how long it took and the memory resources needed.

Limits of Algorithms

• Algorithms have limits, and there are some problems for which we do not have efficient enough algorithms to solve.

• These algorithms can’t run in a reasonable amount of time with our current technology.

• Heuristic approach: This is an approach that may not be optimal or the best but is close enough to use as a solution.

Undecidable/Unsolvable Problems

• A decidable problem is one where an algorithm can be written that results in a correct “yes” or “no” answer for all inputs.

• Determining if a number is prime is an example of a decidable problem.

• An undecidable problem does not have an algorithm that can give a correct “yes” or “no” for all cases of the problem.

Next Chapter:

Chapter 10: Computing Systems and Networks