Diversification and Risky Asset Allocation
Learning Objectives
Understand how to calculate expected returns and variances for a security and a portfolio.
Grasp the significance of portfolio diversification and its impact on risk.
Explore the concept of the efficient frontier and the importance of proper asset allocation.
Diversification
Holding multiple investments can mitigate risk as not all investments will rise or fall in value simultaneously.
Diversification can greatly enhance portfolio return while minimizing risk.
Key questions: How does diversification work, and what are its effects on returns and risks?
Role of Diversification and Asset Allocation
First explored by Professor Harry Markowitz in the 1950s.
An efficiently diversified portfolio maximizes expected return for a given level of risk.
Important to understand how diversification relates to expected returns.
Expected Returns
The expected return is the weighted average of potential returns from the investment over time.
To calculate:
Define possible economic scenarios.
Estimate performance of securities in each scenario.
Assign probabilities to scenarios.
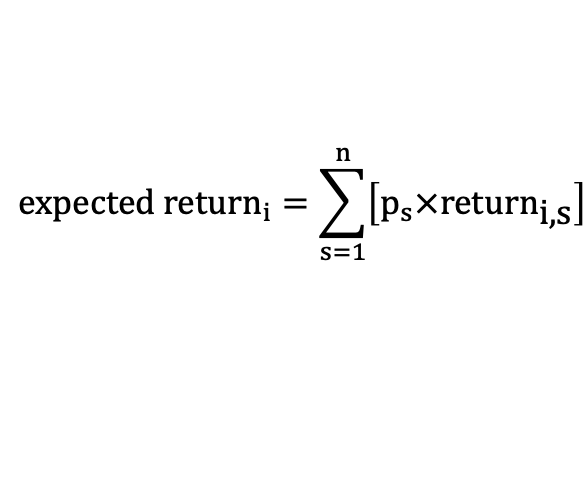
Factors Influencing Stock Choices
Example:
Starcents had an expected return of 25%.
Jpod had an expected return of 20%.
Investors may choose Jpod for lower risk despite a lower expected return.
Expected Risk Premium
Calculated as:
Expected Risk Premium=Expected Return -Riskfree Rate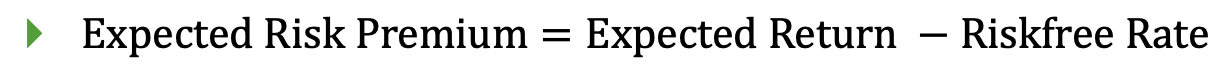
For example, if the risk-free rate is 8%:
Jpod has a premium of 12% (20% - 8%).
Starcents has a premium of 17% (25% - 8%).
Calculating Variance of Expected Returns
Variance measures the dispersion of returns around the expected return.
Formula:
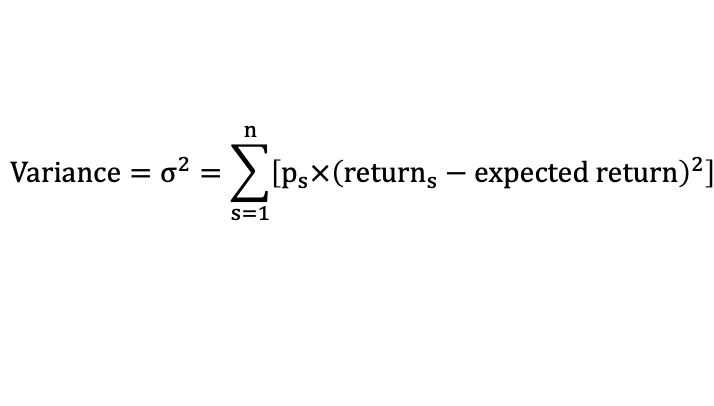
Standard deviation is the square root of variance.
Portfolio Composition
Portfolios consist of multiple assets, and their respective weights indicate the proportion of investment in each.
Expected return of a portfolio is calculated as a weighted average of individual asset expected returns:
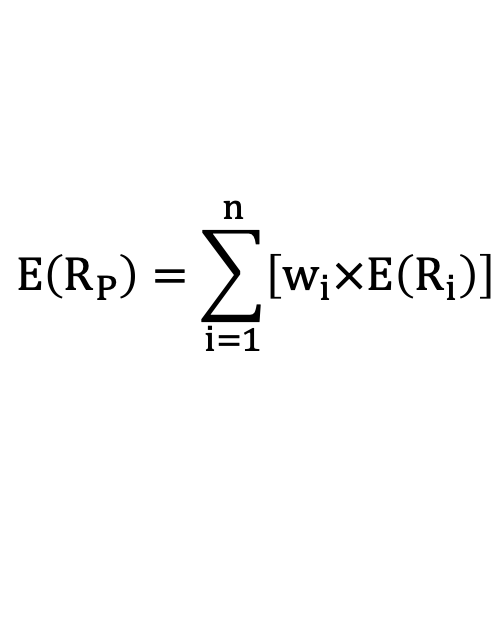
Portfolio Variance Calculations
Variance of a portfolio is not a straightforward weighted average of individual variances.
The formula considers the covariance between asset returns as well.
Diversification and Risk Reduction
Adding more assets reduces diversifiable risk; the portfolio standard deviation decreases with the number of stocks.
Correlation is crucial: less than perfect correlation among assets helps lower overall risk.
The Fallacy of Time Diversification
Misconception that long-term holding of stocks cancels volatility effects.
Historical data shows that volatility of wealth increases over longer periods, contrary to the common belief.
Why Diversification Works
Key factors include the correlation of asset returns; imperfect correlation helps reduce risk.
Correlation coefficients range from -1 (perfect negative) to +1 (perfect positive).
Markowitz Efficient Frontier
Represents the set of portfolios that offer the highest expected return for a given level of risk.
Portfolios below this frontier are considered inefficient as they provide lower returns for the same risk or higher risk for the same return.
Importance of Asset Allocation
Strategic asset allocation involves diversifying investments across different asset classes to optimize returns while managing risk.
Understanding the risk-return profiles of assets is key to constructing an efficient portfolio.