Parameterschätzung

Aufgabe der Parameterschätzung

Grundproblem: Weil durch die Identifikationsgleichungen von überidentifizierten Modellen latente Parameter auf mehr als eine Weise berechnet werden können, resultieren mit den empirischen Daten dann auch unterschiedliche Werte für den gleichen latenten Parameter → keine eindeutige Bestimmung unbekannter Größen möglich

Warum? Modell stimmt nicht oder Modell stimmt in der Population aber unterschiedliche Werte beruhen auf Stichprobenfehlern (also fehlerhaft geschätzte Varianzen/Kovarianzen der manifesten Variablen)

—> Aufgabe der Parameterschätzung: die Populationswerte schätzen unter der Annahme, dass das Modell in der Population gültig ist

Implizierte Kovarianzstruktur

bedeutet: die Strukturgleichungen implizieren ein bestimmtes Größenverhältnis der Varianzen/Kovarianzen der manifesten Variablen (unterschiedliche Modelle implizieren unterschiedliche Kovarianzstrukturen)

Gründe für die Abweichung zwischen empirischer Kovarianzmatrix und implizierter Kovarianzstruktur: 1. Modell ist falsch 2. Modell stimmt in der Population, aber durch Stichprobenziehungen sind Stichprobenfehler entstanden (zufallsbedingte Abweichungen)

→ Modelltest kann klären ob die Abweichungen zufällig sein könnten oder nicht

(kann erst durchgeführt werden, wenn die Modellparameter in der Population geschätzt sind - unter der vorläufigen Annahme, dass das Modell in der Population gültig ist)

“Beobachtete” Kovarianzmatrix \sum

= Schätzung der Populations-Varianzen/Kovarianzen der manifesten Variablen aus den Stichprobendaten (“modellfrei”, also ohne Annahme eines bestimmten Modells)

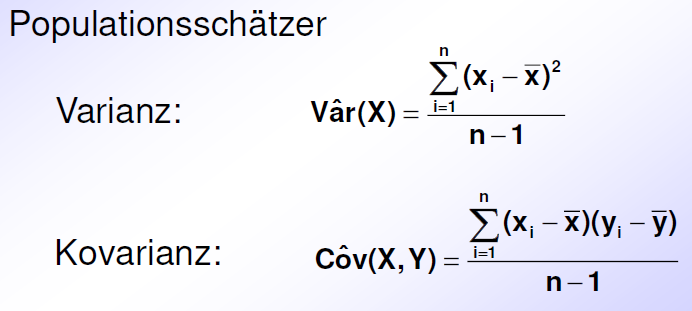
einzelne, nicht-redundante Varianzen/Kovarianzen zwischen den manifesten Variablen = Stichprobenmomente

Matrix der geschätzten Populations-Varianzen/Kovarianzmatrix \sum = “beobachtete” Kovarianzmatrix \sum

Modellparameter \Theta

Was muss geschätzt werden?

• die Varianzen der exogenen Variablen

• Kovarianzen der korrelierten exogenen Variablen

• nicht-fixierte Pfadkoeffizienten

(endogene Variablen lassen sich mit den Strukturgleichungen direkt aus den Varianzen der exogenen Variablen und den Pfadkoeffizienten berechnen)

= Modellparameter

Liste (bzw Vektor) der (nicht redundanten) Modellparameter = \Theta

Implizierte Kovarianzmatrix \sum\left(\Theta\right)

entsteht, wenn Parameter \Theta irgendwie numerisch festgelegt werden und in die Strukturgleichungen eingesetzt werden

Eigenschaften:

• Kovarianzstruktur (durch Strukturgleichungen impliziertes Größenverhältnis der Varianzen/Kovarianzen der manifesten Variablen)

• absolute Größe (durch Modellparameter bestimmte absolute Größe der Varianzen/Kovarianzen der manifesten Variablen)

!! die Kovarianzstruktur ist unabhängig von den Modellparametern (also die Struktur bleibt gleich auch wenn die absoluten Größen sich ändern)

Parameterschätzung

Die Modellparameter können nur dann die gesuchten Populationsschätzer sein, wenn sie gemeinsam mit dem Modell eine Kovarianzstruktur mit folgenden Eigenschaften aufweisen:

• die implizierte Kovarianzmatrix muss die Kovarianzstruktur des Modells aufweisen

• die Elemente der Kovarianzmatrix müssen in ihrer absoluten Größe so ähnlich wie möglich zu der “beobachteten” Kovarianzmatrix sein

Herstellung der Eigenschaften:

• die implizierte Kovarianzmatrix wird sowieso die Kovarianzstruktur aufweisen, solange die Strukturgleichungen des Modells zu ihrer Berechnung verwendet wurde

• die Ähnlichkeit der absoluten Größe der Elemente der implizierten Kovarianzmatrix zur “beobachteten” Kovarianzmatrix hängt von der Wahl der Modellparameter ab

→ Aufgabe: Modellparameter so wählen, dass sie, wenn sie in die Strukturgleichungen eingesetzt werden eine Kovarianzstruktur implizieren, die so ähnlich wie möglich zur “beobachteten” Kovarianzmatrix ist

→ optimale können mit einer “Suchprozedur” gefunden werden

Suchprozedur:

1. Diskrepanzfunktion F[\Sigma,\Sigma(\Theta)] festlegen, welche ein Maß für die (Un-)Ähnlichkeit von “beobachteter” \sum Kovarianzmatrix und implizierter Kovarianzmatrix \sum\left(\Theta\right) liefert

2. (beliebige) Startwerte für die Modellparameter \Theta festlegen

3. Modellparameter mit einem iterativen Algorithmus fortlaufend verändern, so lange bis die Diskrepanzfunktion minimiert ist

→ resultierende Werte für die Modellparameter sind “best guesses” für die Populationsparameter unter der Annahme, dass das Modell in der Population gültig ist

WEIL es gibt keine anderen Werte für die Modellparameter, die die “beobachtete” Kovarianzmatrix unter Beibehaltung der vom Modell implizierten Kovarianzstruktur besser “reproduzieren” könnte als die mit der Prozedur gefundenen Werte

Diskrepanzfunktionen

= eine Funktion der beobachteten Kovarianzmatrix \sum und der implizierten Kovarianzmatrix \sum\left(\Theta\right) → quantifiziert die Diskrepanz (Unähnlichkeit) der beiden Kovarianzmatrizen

es gibt verschiedene:

• Unweighted Least Squares (ULS)

• Generalized Least Squares (GLS)

• Maximum Likelihood (ML)

• Asymptotically Distribution Free (ADF)

• …

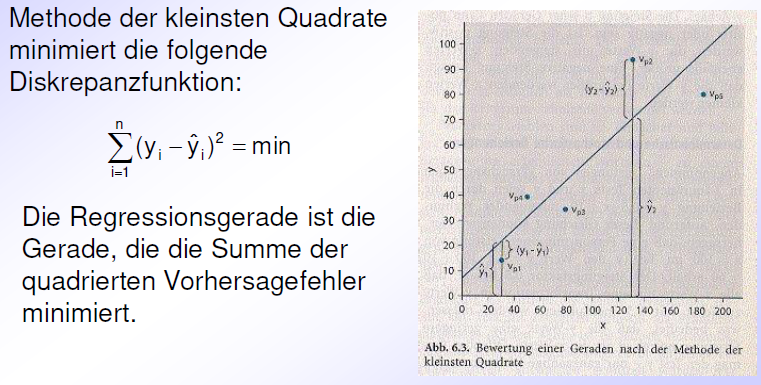
ULS

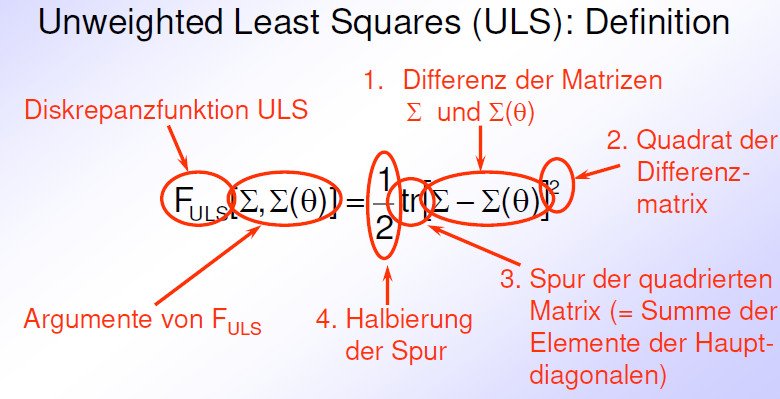
F_ULS Eigenschaften:

• falls die beiden Matrizen identisch sind, ist F_ULS gleich null

• je mehr sich die Elemente der beiden Matrizen unterscheiden, desto größer wird der Wert von F_ULS

• der Wert hängt vom Wertebereich der manifesten Variable ab → deshalb in der Praxis kaum verwendet!!

GLS

GLS Diskrepanzfunktion Eigenschaften:

• falls die beiden Matrizen identisch sind, ist F_GLS gleich null

• je mehr sich die beiden Matrizen gleichen, desto größer wird der Wert von F_GLS

• !!! unabhängig von der Skalenbreite der manifesten Variablen

• !!! lässt sich auf Signifikanz testen

Eigenschaften der mit GLS geschätzten Parameter:

bei großen Stichproben resultieren “gute” Schätzer mit folgenden Eigenschaften

• Konsistenz: mit steigendem Stichprobenumfang konvergieren die Schätzer mit den wahren Populationsparametern

• Erwartungstreue: der Mittelwert über viele Schätzungen ist gleich dem Populationsparameter

• Effizienz: die Schätzer zeigen eine minimale Fehlervarianz

Voraussetzungen für GLS:

• manifeste Variablen müssen eine Intervallskala aufweisen (aber Simulationsstudien lassen vermuten, dass bei einer Ordinalskalierung der manifesten Variablen mit mind. 5 Kategorien und einer NV der Daten GLS approximativ verwendet werden könnte; ansonsten keine praktikable Lösung für ordinalskalierte Daten, weil Analyse mit ADF z.B. mindestens N = 5000 benötigt wird)

• manifeste Variablen müssen in der Population eine multivariate Normalverteilung (NV) aufweisen (hierfür existiert kein strenger Test; kann empfindlich bei Verletzung der NV-Annahme reagieren)

Diagnostik der multivariaten NV über Check der univariaten NV (wenn die nicht gegeben ist, kann multivariat auch nicht sein) über Schiefe und Exzess (Cutoffs: Schiefe 2 und Exzess 7; ggf. Transformation der Variablen zum normalisieren)

PROBLEM: univariate NV impliziert keine multivariate NV → weitere (nich perfekte) Möglichkeiten: Mardia’s Maß des multivariaten Exzess, Mahalanobis-Diastanz für ausreißer

→ Lösung: alternative Verfahren, die keine NV Annahme brauchen wie Bootstrap

ML

Eigenschaften der ML Diskrepanzfunktion:

• falls beide Matrizen identisch ist F_ML gleich null

• je mehr sich die Matrizen unterscheiden, desto größer ist der Wert

• unabhängig von der Skalierung der manifesten Variablen

• maximiert die Wahrscheinlichkeit, dass die geschätzten Modellparameter repliziert werden können, wenn eine neue Stichprobe aus derselben Population gezogen wird

Eigenschaften der geschätzten Modellparameter:

wie bei GLS mit hinreichend großen Stichproben

• Konsistenz

• Erwartungstreue

• Effizienz

Voraussetzungen für ML:

• manifeste Variablen müssen eine Intervallskala aufweisen (gleiche Probleme wie bei GLS

• manifeste Variablen müssen in der Population eine multivariate NV aufweisen (die gleichen Probleme wie GLS, in kleineren Stichproben bei Verletzung der NV ist GLS zuverlässiger)

insgesamt:

Stichprobengröße

Zuverlässigkeit der Parameterschätzung hängt von Stichprobengröße ab

größere Stichprobe und sparsameres Modell → bessere Schätzung

“sparsam” = wenige zu schätzende Modellparameter im Vergleich zur Anzahl der bekannten Stichprobenmomente (Varianzen/Kovarianzen der manifesten Variablen)

erforderliche Stichprobengröße häng ab von:

• Diskrepanzfunktion/Verteilung (GLS: bei Verletzung NV: relativ geringe Stichprobengröße; ML: bei Verletzung NV: ab N=2500 besser als GLS; ADF: ab N = 5000)

• Verhältnis von Indikatoren/Konstrukt in Messmodellen (je weniger Indikatoren pro Konstrukt, desto größer sollte die Stichprobe sein)

• Anzahl der zu schätzenden Modellparameter (pro Parameter mind. 5 VPn)

• allgemein: mind. 100 oder heute ca. 200 VPn

(bei kleinen Stichprobengrößen kann der Effekt der Stichprobengröße auf die Parameterschätzung mit Simulationsstudien überprüft werden (Bootstrap))