OLI - 1. Statements and arguments
- Logic is the study of principles of correct reasoning.
- Logic is interested in the kind of arguments one gives as a reason for accepting the truth of some particular claim.
- Arguments are pervasive in every aspect of human life.
- The logician is not interested in the subject matter of the argument, rather argument itself, the pattern of reasoning that it embodies.
Statements
- The conclusion of the argument: the particular claim that an argument is for.
- The whole purpose of an argument is to provide a reason for accepting the truth of its conclusion
- Statement: something that has to be either true or false, and can't be both.
- The same statement can be expressed by many different sentences.
- Ej: I have been here before, It's not the first time I've been here, He estado aquí antes.
- Other types of sentences
- Declarative: statements.
- Indexical: might be true while others are false depending on who utters the sentence, and when and where.
- Ambiguous: a single sentence can be associated with multiple statements
- Non-declarative: can't be considered true or false. Interrogative, imperative and exclamations.
Premises and conclusions
- Premises: set of statements, the reason for accepting the truth of the conclusion.
- The argument is made up of premises and a conclusion.
- To identify the conclusion: what claim is the argument's presenter trying to convince you is true?
- To identify the premise: what support is the argument's presenter providing for the truth of the conclusion?
- An explanation simply provides information, it doesn't attempt to establish the truth of a statement.
- A definition defines a word or phrase.
- A description provides a mental image of the object or situation being described.
- Determine what the passage is doing to know if it is an argument or just an explanation.
- An argument will try to persuade.
- Rethorical questions and imperatives may sometimes pose as an argument.
Identifying conclusions and premises
- If there is one statement that the author of an argument is going to distinguish as being special, it is the conclusion.
- To identify a conclusion:
- Sometimes the author may explicitly state the conclusion.
- They are often stated first and/or last.
- May be indicated via conclusion indicator words
- therefore
- thus
- hence
- so
- consequently
- as a result
- it follows that
- this shows/indicates/means/implies that
- Identify all the premises, and the statement left will be the conclusion.
- To identify a premise:
- Identify the conclusion, and everything else will be a premise.
- Indicator phrases like
- consider that
- take as evidence that
- it is evident that
- it is a fact that
- recall that
- Premise as clause indicators
- since
- because
- for the reason that
- as
- inasmuch as
- as indicated by
Arguments in standard form
Standard form of an argument: write out all the premises first, then separate the conclusion by drawing a line and setting the symbol ∴ (therefore).
Example:

Why premises and conclusions aren't enough
- What makes an argument a good argument
- The premises should be true
- Valid: any argument where the truth of the premises makes it impossible for the conclusion to be false
- Inductively strong: an argument where the truth of the premises does not guarantee the truth of the conclusion, but rather makes it highly probably to be true
- The premises of the argument should actually support the truth of the conclusion
- Sound: arguments that are valid and have true premises
- Cogent: arguments that are strong and have true premises
- Not all valid/strong arguments are sound/cogent (since some or all of their premises could be false), but any sound/cogent argument is necessarily valid/strong.
Symbolic or formal logic
- The structure of an argument crucially involves the logical structures of the premises and conclusion, as well as the pattern of relationships that hold between them.
- The content of statements is of no consequence for (logical) arguments.
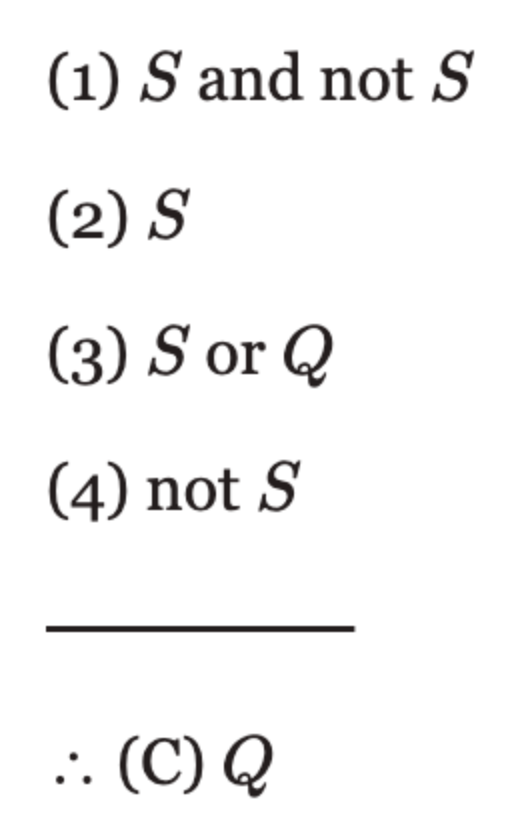
- Each step of the argument is a fundamental pattern or rule of inference that can be applied any time we deal with sentences of the appropriate form.
Proofs
- Proof: an argument that demonstrates its conclusion by a series of logical steps.
Argument diagramming
- Argument diagrams allow us to represent more than just premises and conclusions.
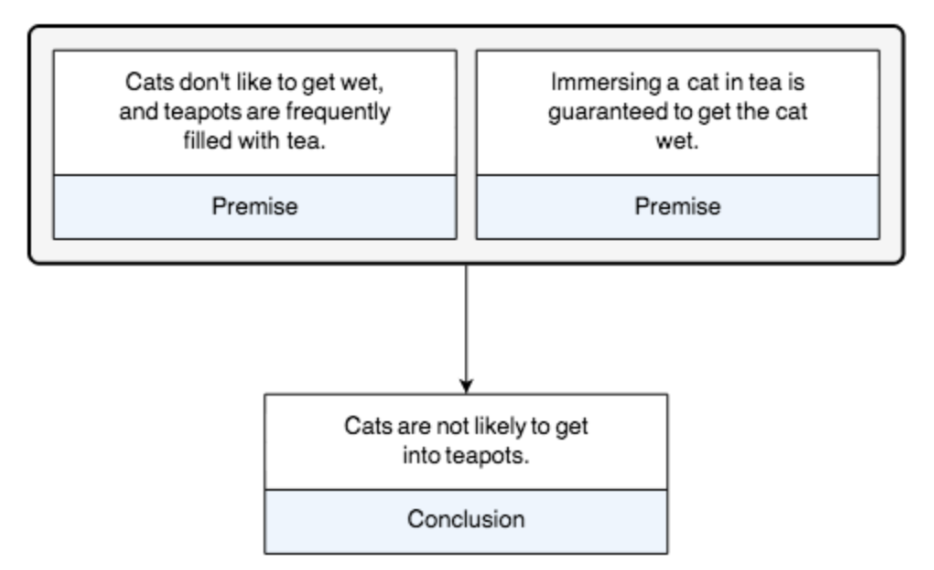
- Each premise is independent, together (joint) they support the conclusion.
Summary
- Chapter overview, including an introductory movie and a statement of the learning objectives for the chapter ahead.
- Declarative sentences express statements, which can be either true or false. Statements are the pieces out of which arguments are constructed.
- Arguments consist of premises and a conclusion, each of which is a statement. Non-arguments have neither premises nor conclusion.
- We discuss various techniques, including the use of particular words and phrases, for indicating that a particular sentence is the conclusion of an argument. As with conclusions, various techniques, including specific words and phrases, indicate that a particular sentence serves as a premise of an argument. Also considered are premises and conclusions that appear as clauses within the same sentence.
- Arguments can be presented in a standard form that clearly indicates what the premises and conclusion of the argument are.
- First, the criteria by which an argument may be considered good or bad are discussed. With that done, examples are compared to illustrate why representing an argument as just a set of premises and conclusion isn't enough to allow a reasonable logical analysis of the argument, and what we need to add to address this deficiency is discussed.
- The motivation for adopting a symbolic approach to logic is discussed.
- Two interesting and historically important proofs are presented as an illustration of the intricate structure an argument can have.
- Argument diagrams are introduced as an alternative to standard form for representing arguments. Premises can provide support for a conclusion either jointly or independently; the technique for reflecting these differences in argument diagrams is discussed.
New terms
| argument | conclusion | statement | premise | conclusion |
|---|---|---|---|---|
| premise | explanation | definition | standard form | valid |
| inductively strong | sound | cogent | invalid | argument diagrams |