Waves
Types of waves
Waves that pass through a substance = vibrations passing through a substance
Mechanical waves = oscillations of particles, so transfer energy through a medium
Electromagnetic waves = oscillating electric and magnetic fields, no medium needed
Longitudinal and Transverse waves
Longitudinal = oscillations are parallel to the direction of propagation
Transverse = oscillations are perpendicular to the direction of propagation
Polarisation
Only happens to transverse waves
Unpolarised = oscillations can change from one plane to another
Polarised = oscillations stay in one plane only
Polarising filter only allows light through which vibrates in a certain direction - so becomes polarised
Unpolarised light —> 2 polaroid filters —> Light intensity of transmitted light changes if one polaroid is turned to an angle of the other. If filters are at 90*, then transmitted particles of first filter are at 90* to the second filter, so the light intensity is minimum - ‘crossed’ —> polarised light from first filter cannot pass through second filter.
Polaroid sunglasses reduce the glare of light reflected —> light is polarised, Intensity reduced.
Plane of Polarisation of EM Waves: The plane in which the electric field oscillates
Key terms of measuring waves
Displacement = distance and direction from equilibrium position
Amplitude = the maximum displacement of a vibrating particle
Wavelength = the smallest distance between 2 adjacent vibrating particles with same s and V
Cycle = one max displacement to the next max displacement
Period = time for one complete wave to pass a fixed point
Frequency = the amount of waves passing through a fixed point per second
T = 1/f
Wave Speed
Higher frequency = shorter wavelength
C = fλ
Phase Difference
Phase of a vibrating particle = the fraction of a cycle it has completed since the start of the cycle
Phase difference of two particles vibrating at the same frequency = fraction of a cycle between the two particles
1 cycle = 360* = 2π
phase difference = 2πd/λ (where d is the distance between the 2 points on a wavelength)
Superposition
The principle of superposition = when two waves meet, the total displacement at a point is equal to the sums of the individual displacements at that point
crest + crest = supercrest (reinforcement)
trough + trough =supertrough (reinforcement)
crest + trough (of same amplitude) = minimum (cancellation)
Interference happens when waves pass through each other at a constant frequency and phase difference cancel and reinforce at fixed positions
Coherent waves = same frequency and constant phase difference
Formation of Stationary Waves
A progressive wave is produced on one end of a source
Another wave reflects back in the opposite direction to the progressive wave
Both waves are at the same frequency
They interfere and superpose to form a maximum displacement at antinodes and minimum at nodes
The nodes are at fixed points along the wave
Node = position of no displacement
Antinode = position of maximum displacement
First harmonic = fundamental frequency = 2 nodes and 1 antinode
Distance between nodes (hence length) on a first harmonic frequency = λ/2
To form a 2nd harmonic: increase the frequency 2x, so wavelength halves
Length of rope on a second harmonic frequency = λ
Amplitude of vibration = 0 at nodes = 0 energy
Amplitude of vibration = max at antinodes = max energy
Nodes and Antinodes are at fixed positions, no energy is transferred.
Stationary vs progressive waves
Stationary = all particles except the nodes vibrate at the same frequency
Progressive = all particles vibrate at the same frequency
Stationary = amplitude varies from 0 at nodes to max at antinodes
Progressive = amplitude is the same for all particles
Stationary = phase difference is equal to mπ, where m is the number of nodes between the 2 particles
Progressive = phase difference is equal to 2πd/λ
Harmonics
First harmonic = lowest frequency that produces an interference pattern
1 antinode in middle
2 nodes at either end
L = λ/2
f = c/2L
Second harmonic = 2 antinodes, and 3 nodes (1 in middle, and 2 at ends)
f = c/L
Third harmonic = 3 antinodes, 4 nodes
f = 3c/2L
Second harmonic frequency = 2 x first harmonic frequency
Third harmonic frequency = 3 x first harmonic frequency
The length (L) of a vibrating section of a string = mλ/2
Where m is a whole number (the number of nodes between the vibrating section)
Pitch is altered directly by frequency
Increase Tension/shorten length = increase pitch
Decrease Tension/increase length = decrease pitch
f = 1/2L x root(T/mew) where mew is mass per unit length
Refraction of light
Refraction = change in direction that occurs when light passes at an angle across a boundary between 2 transparent surfaces
Air —> glass = towards normal - slows down (because less dense —> more dense)
Glass —> air = away from normal - speeds up (because more dense —> less dense)
air = 3×10^8
glass = 2×10^8
if passes into a more dense substance —>bends toward normal
if passes into a less dense substance —> bends away from normal
Refraction from air to glass
Angle of refraction is always less than angle of incidence
Partial reflection also occurs.
Snell’s law = refractive index = sin(i)/sin(r.)
Refractive index is portrayed through the letter ‘n’
Absolute refractive index = ratio between speed of light in a vacuum to speed of light in a material - always greater than 1, as no material is less optically dense than a vacuum
Relative Refractive Index = ratio between the speed of light in one material compared to the speed of light in another - can be greater than 1
Refraction in Prims

More Refraction
The amount of refraction depends on the speed of the waves in each substance
sin(i)/sin(r.) = C/Cs (where Cs is the speed of light in the substance)
so Ns = C/Cs (where Ns is the refractive index of the substance)
so the smaller the speed of light in a substance, the greater the refractive index of the substance
The frequency of the wave DOES NOT CHANGE when refraction occurs, but the wavelength does. so Ns = λ/λs (where λs is the wavelength of the wave in the substance).
Refraction at the boundary of 2 transparent substances
sin(i)/sin(r.) = C2/C1
n1sinθ1 = n2sinθ2
Refractive Index of Air
C in air is approximately 99.97% the C in a vacuum
So refractive index of air = 1.0003 but is recalled as approximately 1
White Light Spectrum
A prism splits a beam of light into the colours of the spectrum
Red (650nm) - Violet (350nm)
The prism refracts the light at different amounts depending on the wavelength
The Shorter the Wavelength (in air) the greater the refraction, so each colour is diffracted by a different amount.
The dispersive effect occurs because the speed of light in glass depends on wavelength (slower = lower wavelength = greater refraction) therefore violet has a greater refractive index, and red has a lower refractive index.
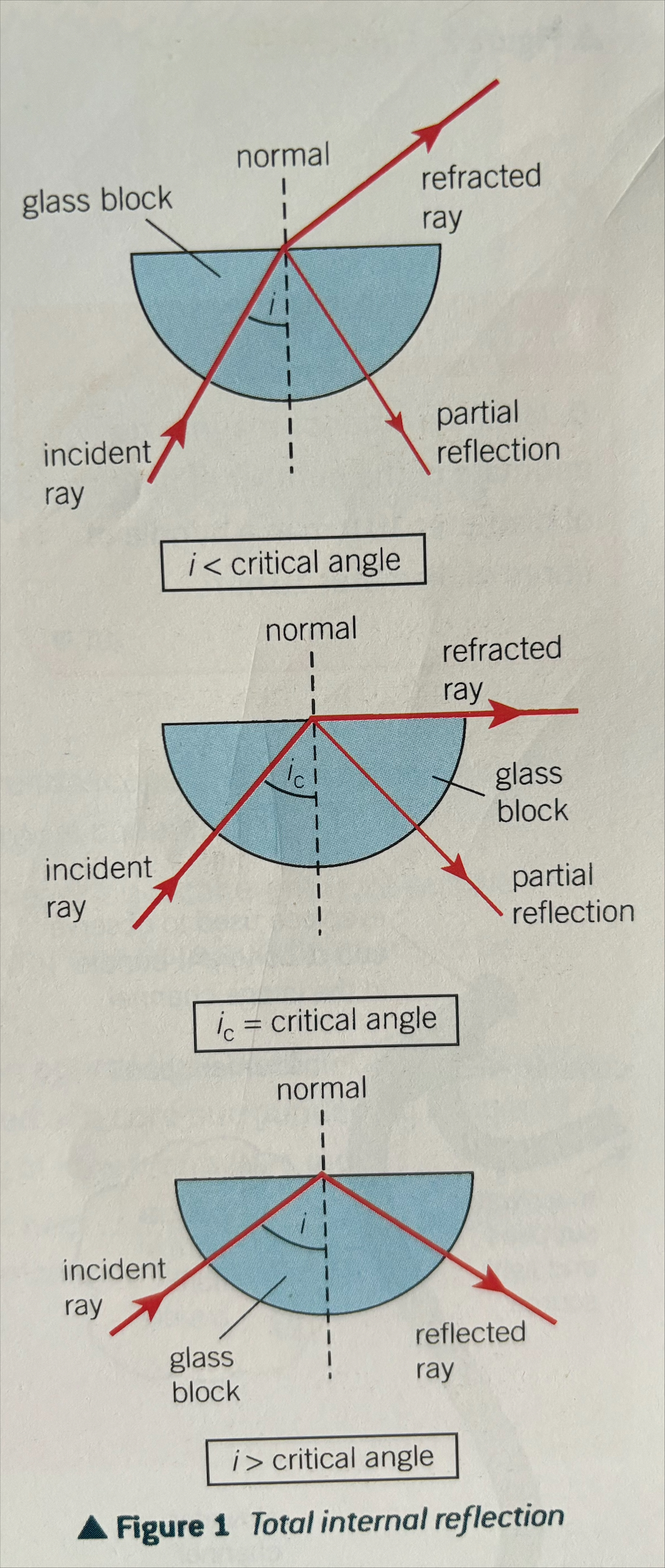
Total Internal Reflection
Glass —> air, ray refracts away from normal
If angle of incidence = critical angle, then it refracts across the boundary of the glass (and there is still some partial reflection - as partial reflection always occurs when the angle of incidence is less than or equal to the critical angle)
If angle of incidence > critical angle, then the ray undergoes total internal reflection (same as reflection of a mirror)
if angle of incidence = critical angle, then refraction is 90* to the normal
Total Internal Reflection can only take place if the incident substance has a larger refractive index than the other substance (in this case glass has a greater refractive index than air) AND the angle of incidence exceeds the critical angle
Sinθc = N2/N1
Diamonds sparkling
light enters diamond - splits into the colours of the spectrum
Very high refractive index, so the colours are separated a lot
Because of the high refractive index, the ray of light undergoes total internal reflection many times before it emerges from the diamond
so the colours disperse more and more, and the diamond sparkles with many colours
Optical Fibres
A light ray is totally internally reflected each time it reaches the fibre boundary, because the angle of incidence exceeds the critical angle of the fibre
It might not reflect totally if the radius of the bend of the fibre is too small
FOR COMMUNICATIONS - pulses of light enter from one end at a transmitter, and reach a receiver at the other end.
Fibres need to be highly transparent to avoid the absorption of light (absorption can continuously reduce the amplitude of the light)
Each fibre consists of a core surrounded by a layer of cladding. The cladding has a lower refractive index to reduce light loss from the core (as this could reduce the amplitude of the light pulses)
Total Internal Reflection takes place at the core-cladding boundary
If there was no cladding, the light would cross from one fibre to the other if 2 fibres are in contact - signals would corrupt and be insecure, as would reach the wrong destination
The core should be narrow to prevent modal (multipath) dispersion - it happens in a wide core because the light travelling along the axis of the core travels a shorter distance per metre of fibre compared to a ray that is repeatedly totally internally reflected. Also, a pulse of light sent via a wide core would become longer than it was supposed to be, and if it is too long, it may merge with the next pulse
Dispersion of pulses also occurs if white light is used instead of monochromatic light - material/spectral dispersion. (the speed of light in the optical fibre depends on the wavelength of light. Violet travels slower than red in glass, and so the difference in speed causes the white light pulses to become longer - as the violet component falls behind the red component - so we must use monochromatic light.
FOR MEDICAL ENDOSCOPES - contains 2 bundles of fibres
inserted into a body cavity, and illuminated using light sent through one of the bundles
A lens over the other bundle is used to form an image of the cavity on the end of the bundle - the light then travels in pulses to the other end of the bundle, where the image is observed. The bundle must be a coherent bundle - fibres at each end are in the same relative position.
Double slit interference
Young’s fringes - alternate bright and dark fringes can be seen on a white screen due to where the diffracted light from the double slits overlap - evenly spaced and parallel to the double slits
If the single slit is too wide, then the dark fringes become narrower than the bright fringes, and contrast is lost between dark fringes and bright fringes
Fringes form due to the interference of light
bright fringe - light from one slit reinforces the light from the other - arrive in phase with each other
Dark fringe - light from one slit cancels the light from the other - π out of phase
w = λD/s
w = fringe separation
D = distance from slits to the screen
s = slit spacing = distance between the centres of the slits
Increase fringe width
increase wavelength
increase Distance
decrease slit spacing
More on interference
double slits are coherent sources of waves as they emit waves of the same frequency and a constant phase difference
2 nearby light bulbs cannot form interference, as the two sources emit waves at random, so the points of cancellation and and reinforcement would change at random.
Fringe separation also depends on colour of light used - each have their own wavelength.
red - longest wavelength - greatest separation
White light fringes have the central fringe as white. Inner fringes are blue and outer fringes are red. This is because the red fringes are more spaced out than the blue fringes and the two fringe patterns do not overlap directly.
Diffraction
The spreading of waves when they pass through a gap
Wide gap — less diffraction
Small gap — more diffraction
Increase diffraction — decrease gap
Increase diffraction — increase wavelength
Single slit diffraction
Shows a central fringe with further fringes on either side of the central fringe
Central fringe is twice as wide as the outer fringes
Peak intensity of each fringe decreases with distance from the centre
Each of the outer fringes have the same width
Outer fringes are less intense than the central fringe
Increase wavelength — increased width between fringes and maxima
decrease slit width — increase width of fringes, and lower intensity of light
W = λ2D/a (where W=width of central fringe, a=width of single slit, D=distance of screen and slit)
The Diffraction Grating
A plate with many closely placed parallel slits ruled on it
If monochromatic light is directed normally at a grating, light is only transmitted in certain directions: light passing through each slit is diffracted, and diffracted light waves from adjacent slits reinforce each other in certain directions only (including the incident direction), and cancel out in all other directions
The central beam is the zero order beam — it is in the same direction as the incident beam (n=0)
angle of diffraction between transmitted beam and central beam increases if greater wavelength is used, or narrower slits are used on the grating.
dsinθ = nλ (d=grating spacing, n=nth order)
N (number of slits per metre) = 1/d
Larger number of slits per metre = bigger angle of diffraction
Max number of orders produced use theta as 90. (then round down)
Number of Maxima observed is 2n+1