Two Dimensional Kinematics
Vectors
- Quantities with both magnitude and direction
- Magnitude is a number value (with units)
- Directions can be compass points, left, right, up, down, etc.
- You can assume that every vector makes a right angle. You can use trigonometry to find the resultant vector (R).
- This is the sum of both vectors.
- To subtract a vector you add the negative of that vector.
- The negative of that vector has an opposite direction (180)
Projectile Motion
Projectile motion describes objects travelling through space under the influence of gravity
This applies from when the object is launched to right before it hits the ground
==The only force is the weight (force of gravity)==
Ay = -9.80 m/s
Ax = 0 m/s
In the X-Axis we can only use the equation vx = x/t
In the Y-Axis we can use 4 kinematic equations:
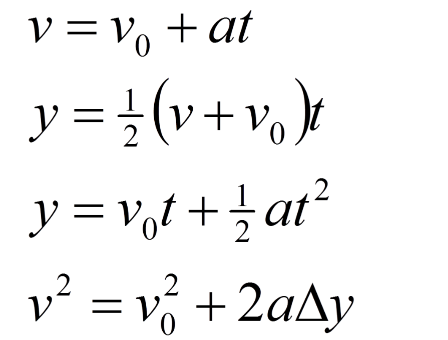
The easiest way to solve for projectile motion is to use a table!
Example: If a projectile was launched at 22 m/s at an angle of 35 what is the displacment after 2.50s?
| X | Y | ||
|---|---|---|---|
| Vx: | 22cos35 = 18.0 | Voy: | 22sin35 =12.6 |
| x: | 18.0/2.50 = 45.0 m | Vy: | |
| t: | 2.50s | t: | 2.50s |
| a: | -9.80 m/s | ||
| y: | (12.6)(2.5) + 1/2(-9.8)(2.5)^2 = .88m |
- The displacement can now be solved for using vector trigonometry
- Take the square root of 45^2 and .88^2 = 45m
Uniform Circular Motion
Uniform circular motion describes objects moving in a circular path with a constant speed. The magnitude of the velocity is a constant.
At any moment the direction of the velocity is tangent to the path that it is following
This is called the tangential velocity
The magnitude can be found using: v = d/t → 2πr/T
==Acceleration can cause a change in direction but does not change the magnitude of the velocity==
It is always directed towards the center of the path
Centripetal means directed to the center
Centripetal acceleration can be found using v^2/r
Example: A car traveling at 25.0 m/s around a curve with radius 15 meters
If we were to find the centripetal acceleration we use Ac = v^2/r
Ac = 25^2/15 = 42 m/s