Forces (OCR)

Motion

Describe how to measure distance and time in a range of scenarios

Distance Measurement Techniques:

• Using a ruler or tape measure – for short, straight distances (e.g., length of a desk).

• Trundle wheel – for longer distances, like a school corridor.

• Measuring wheel or GPS device – for large-scale distances (e.g., running track).

• Ultrasonic sensor or laser rangefinder – for accurate measurements, especially indoors or in physics experiments.

Time Measurement Techniques:

• Stopwatch – commonly used for manual timing (human reaction time limits accuracy).

• Light gates – for more precise timing, especially in experiments (object passes through a beam).

• Ticker timer – old but useful in classroom experiments to study motion.

Scenarios:

• Measuring how far and how fast a toy car travels.

• Timing a person running a set distance.

• Dropping a ball and measuring time taken to hit the ground.

Describe how to measure distance and time and use these to calculate speed 

Speed Calculation:

From Distance-Time Graphs:

• Straight line → constant speed. Gradient = speed.

• Steeper line → higher speed.

• Curved line → changing speed (acceleration or deceleration).

• Flat line → object is stationary.

Make calculations using ratios and proportional reasoning to convert units and to compute rates

Key Conversions:

• Distance:
  1 km = 1000 m
  1 m = 100 cm

• Time:
  1 minute = 60 seconds
  1 hour = 3600 seconds

• Speed Units:

  • Convert km/h to m/s: divide by 3.6
    e.g. 90 km/h → 90 ÷ 3.6 = 25 m/s

  • Convert m/s to km/h: multiply by 3.6

Rates and Ratios:

• Use proportional reasoning when comparing speeds, times, or distances.

• Example: If speed doubles, time to travel the same distance halves.

Explain the vector–scalar distinction as it applies to displacement and distance, velocity and speed

Scalars:

• Have magnitude only.

• Examples: distance, speed, time, energy.

Vectors:

• Have magnitude and direction.

• Examples: displacement, velocity, acceleration, force.

Key Differences:

• Distance vs Displacement:

  • Distance: total path travelled (scalar).

  • Displacement: shortest straight-line path from start to end (vector).

• Speed vs Velocity:

  • Speed: how fast something moves (scalar).

  • Velocity: speed in a given direction (vector).

Relate changes and differences in motion to appropriate distance-time and velocity-time graphs; interpret lines and slopes

Distance-Time Graph:

• Gradient = speed

• Curved line: acceleration.

• Flat line: stationary object.

Velocity-Time Graph:

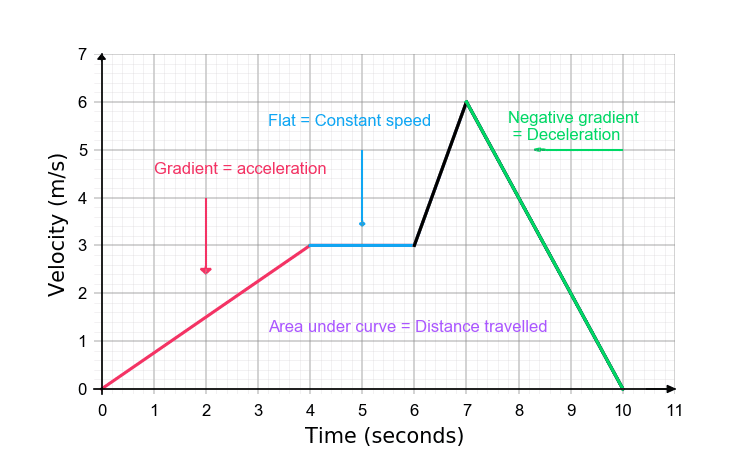
• Gradient = acceleration

• Flat line = constant velocity.

• Line sloping up = acceleration.

• Line sloping down = deceleration.

Interpret enclosed area in velocity-time graphs

Key Concept:

• Area under velocity-time graph = distance travelled

Calculations:

Calculate average speed for non-uniform motion

Key Concept:

When an object moves with non-uniform motion, its speed changes over time. Average speed helps describe its overall rate of movement.

Example:

A cyclist travels:

• 4 km in 20 minutes,

• then 6 km in 30 minutes.

Total distance = 4 + 6 = 10 km
Total time = 20 + 30 = 50 minutes = 50 ÷ 60 = 0.83 hours

Apply formulae relating distance, time and speed, for uniform motion, and for motion with uniform acceleration

Uniform Motion:

For objects moving at a constant speed:

Uniform Acceleration:

When acceleration is constant, use the SUVAT equations:

When to Use:

• These apply when motion has constant acceleration (like free-fall under gravity, ignoring air resistance).
  

  

Newton’s Law

Recall examples of ways in which objects interact

Key Types of Interactions:

1. Contact Forces:

   • Normal contact force: Acts perpendicular to surfaces in contact (e.g., book on a table).

   • Friction: Acts parallel to surfaces and opposes motion (e.g., sliding a box).

   • Tension: In ropes or strings.

   • Air resistance (drag): Opposes motion through air.

2. Non-contact Forces:

   • Gravitational force: Attraction between masses (e.g., Earth and a ball).

   • Electrostatic force: Between charged particles (e.g., comb attracting paper).

   • Magnetic force: Between magnets or magnetic materials (e.g., compass and magnet).

Describe how such examples involve interactions between pairs of objects which produce a force on each object

Newton’s Third Law:

"For every action, there is an equal and opposite reaction."

Examples:

• A person pushing a wall → wall pushes back on the person.

• A book on a table → book pushes down (weight), table pushes up (normal force).

• Magnet attracting a nail → nail pulls back on the magnet with equal force.

Each force acts on a different object, but they are equal in size and opposite in direction.

Represent forces as vectors

Vectors in Force Representation:

• Direction of arrow = direction of force.

• Length of arrow = magnitude of force.

Free Body Diagrams:

• Show all forces acting on one object.

• Examples of common forces in diagrams:

  • Weight (W or mg): downwards

  • Normal contact force (N): upwards from surface

  • Friction: against motion

  • Tension: along rope or string

  • Thrust or applied force: in direction of motion

Apply Newton’s First Law to explain motion of objects

Newton’s First Law of Motion:

"An object will remain at rest or move with constant velocity unless acted on by a resultant force."

Applications:

• No resultant force → object stays still or moves at constant velocity.

• Resultant force present → object changes speed and/or direction (accelerates or decelerates).

Examples:

• A car cruising at constant speed → driving force equals resistive forces.

• A ball slowing down → unbalanced force (friction) opposes motion.

Use vector diagrams to illustrate resolution of forces, a net force (resultant force), and equilibrium situations

Key Concepts:

• Resultant force: The single force that has the same effect as all the individual forces acting on an object.

• Equilibrium: All forces are balanced → resultant force = 0.

Vector Diagrams:

• Use scale drawings to add forces.

• Forces can be added tip-to-tail.

• Only parallel and perpendicular vectors are required for this course.

Examples:

1. Two forces at right angles → use a right-angled triangle.

2. Object hanging from two cables → resolve forces horizontally and vertically.

Describe examples of the forces acting on an isolated solid object or system

Key ideas:

• Forces are vector quantities that can act in various directions.

• An isolated object means we only consider forces acting on the object, not those it exerts.

• Examples include:

  • Skydiver:

    • Initially accelerates due to weight (gravity) > air resistance.

    • As speed increases, air resistance increases.

    • Eventually, air resistance = weight → terminal velocity (no acceleration).

  • Vehicles:

    • Car moving at constant speed: driving force = resistive forces (air resistance + friction).

    • Braking: unbalanced force opposite to motion causes deceleration.

Describe, using free body diagrams, examples where two or more forces lead to a resultant force on an object

Key ideas:

• A resultant force is the single force that has the same effect as all forces acting together.

• Free body diagram (FBD): a diagram showing all the forces acting on an object (arrows labelled with size and direction).

Examples:

1. Falling object: weight down, air resistance up → resultant force downwards → acceleration down.

2. Car accelerating: driving force forward, resistive force backward → resultant force forward → acceleration.

3. Tug of war: unequal forces → object moves in direction of larger force.

Important concepts:

• Use vector addition for resultant force.

• Direction and magnitude both matter.

Describe, using free body diagrams, examples of the special case where forces balance to produce a resultant force of zero (qualitative only)

Key ideas:

• When forces are balanced, the resultant force is zero.

• The object is either:

  • Stationary, or

  • Moving at a constant velocity (Newton’s First Law).

Examples:

1. Book resting on table:

   • Weight down, normal contact force up → balanced.

2. Parachutist at terminal velocity:

   • Air resistance = weight → no acceleration.

3. Car cruising at constant speed:

   • Driving force = resistive force.

( FBD should show equal and opposite forces. )

Apply Newton’s Second Law in calculations relating forces, masses, and accelerations

Newton’s Second Law:

F = ma

Where:

• F = resultant force (N)

• m = mass (kg)

• a = acceleration (m/s²)
  

Calculations:

• Given any two of the values, solve for the third.

• Acceleration is in the direction of the resultant force.

Examples:

Inertia and inertial mass

Key ideas:

• Inertia: the tendency of an object to resist a change in its motion (whether starting, stopping, or changing direction).

• Objects with more mass have more inertia.

• Inertial mass is defined as:
  

  

• This means an object requiring more force to accelerate has more inertial mass.

Example:

• A truck requires more force to accelerate than a small car due to greater inertial mass.

Momentum and collisions

Key ideas:

• Momentum (p) is a measure of how much motion an object has:
  

  

• Law of conservation of momentum:

  • In a closed system (no external forces), total momentum before = total momentum after a collision.

Examples:

• Two trolleys colliding and sticking together.

• A gun recoiling when firing a bullet (momentum is conserved).

Inter-relationships between force, mass, velocity, and acceleration

Relevant equations:

• Changes in force or mass will affect acceleration and velocity.

Example:

• Increasing force on the same mass increases acceleration.

• Reducing mass while keeping force constant also increases acceleration.

Work done, force, and distance

Equation:

• Work done = energy transferred.

Example:

• Lifting a box: force = weight, energy is transferred to gravitational potential energy.

Stored energy and energy transfers

Key formulas:

Example:

• A falling object transfers GPE into KE.

Power

Definition:

• Power = rate of energy transfer:
  

  

Example:

• A powerful motor transfers more energy per second.

Newton’s third law

Law: "For every action, there is an equal and opposite reaction."

Key idea:

• Forces always come in pairs, acting on different objects.

Examples:

• Pushing against a wall: the wall pushes back equally.

• A swimmer pushes water backward; water pushes the swimmer forward.

Applications:

• Helps explain equilibrium (balanced forces) and non-equilibrium (resultant forces).

Circular motion with constant speed

Key idea:

• Even if speed is constant, velocity changes because the direction changes.

• This means there is acceleration (called centripetal acceleration).

• A centripetal force is required to keep the object moving in a circle.

Examples:

• Car turning around a bend.

• Satellite orbiting Earth.

• Ball on a string being whirled in a circle.

Forces in Action

Explaining deformation (stretch, bend, compress)

Key idea:
To deform (change the shape of) an object by stretching, bending, or compressing, more than one force must be applied. This is because:

• A single force would simply cause motion (according to Newton's laws), not deformation.

• To stretch something, you need equal and opposite forces pulling it apart.

• To compress something, you need equal and opposite forces pushing it together.

• To bend an object, you need a combination of forces in different directions (a turning effect).

Examples of real-life applications:

• Stretching a spring: requires pulling from both ends.

• Compressing a sponge: involves squeezing forces from opposite sides.

• Bending a ruler: one end pushed up, the other down.

• Suspension in vehicles: uses springs that stretch and compress under load.

• Bridges and beams: experience bending forces under weight.

Elastic vs. plastic deformation

Elastic deformation:

• The object returns to its original shape when the force is removed.

• Occurs when the material is within its elastic limit.

• Energy is stored as elastic potential energy and is fully recoverable.
  

Plastic deformation:

• The object does not return to its original shape after the force is removed.

• It has been permanently deformed.

• Happens when the material is stretched beyond its elastic limit.

Example comparison:

Describe the relationship between force and extension for a spring and other simple systems

• Hooke’s Law:
  In many simple systems like springs, the extension (or compression) is proportional to the force applied, provided the limit of proportionality is not exceeded.
  Mathematically:

• Graphical representation:

  • A force vs extension graph for a spring initially shows a straight line through the origin (linear region).

  • The gradient of this straight section represents the spring constant k.

  • After a certain point (called the limit of proportionality), the graph curves, showing the spring has entered a non-linear behavior.

• Other systems:

  • Elastic bands, bungee cords, or other elastic materials also show force-extension behavior but may not obey Hooke’s Law precisely.

Describe the difference between linear and non-linear relationships between force and extension

• Linear relationship:

  • Force and extension are directly proportional.

  • The graph is a straight line through the origin.

  • The object obeys Hooke’s Law.

  • Examples: Springs within the elastic limit.
    

• Non-linear relationship:

  • Force and extension are not proportional.

  • The graph curves.

  • The object does not obey Hooke’s Law beyond the limit of proportionality.

  • Behavior becomes plastic (permanent deformation) or the material fractures if force is too large.

Calculate a spring constant in linear cases

• From the linear portion (before the limit of proportionality), the spring constant kkk is calculated using:
  

  

  ​

• Units:

  • Force F in newtons (N).

  • Extension e in meters (m).

  • Spring constant k in newtons per meter (N/m).
    

• Example calculation:
  If a force of 10 N produces an extension of 0.05 m:
  

  

Calculate the work done in stretching

• Work done is the energy transferred when a force causes an object to stretch (or compress).

• Formula for work done in stretching a spring:

• Important:
  

  

Describe that all matter has a gravitational field that causes attraction, and the field strength is much greater for massive objects

• Key idea:
  All matter exerts a gravitational force on other matter.

• Gravitational field:

  • A region in which another object will experience a force of gravitational attraction.

  • Field strength depends on the mass of the object — larger masses have stronger gravitational fields.

• Example:

  • The Earth's gravitational field is strong because of its large mass.

Define weight, describe how it is measured, and describe the relationship between the weight of an object and the gravitational field strength ggg

• Weight:

  • The force due to gravity acting on an object.
    

    

• Key facts:

  • Mass is constant (same everywhere).

  • Weight depends on the gravitational field strength.

  • On Earth,

• Measurement:

  • Weight is measured using a newtonmeter or spring balance.
    

Recall the acceleration in free fall

• Free fall:
  When only gravity acts on an object (ignoring air resistance).

• Acceleration in free fall near Earth's surface:
  

  

  
  (You can also see g approximated as 9.8 m/s² in more precise calculations.)
  

• Meaning:

  • An object in free fall accelerates downwards at 10 m/s².

Apply formulae relating force, mass, and relevant physical constants (including ggg) to explore how changes in these are inter-related

• Key formulae:

  

• Understanding interrelations:

  • Increase mass → increase weight (if ggg constant).

  • Increase force → increase acceleration (if mass constant).

• Examples:

  • Doubling the mass while keeping g constant doubles the weight.

  • On the Moon, where g is smaller (~1.6 N/kg), objects weigh less even though mass is unchanged.

Describe examples in which forces cause rotation

• Moments (turning effects):

  • A force applied at a distance from a pivot point causes rotation.

• Moment formula:
  

  

  • Moment measured in newton meters (Nm)

• Direction:

  • If the force tends to cause clockwise rotation, it's called a clockwise moment.

  • If the force tends to cause anticlockwise rotation, it's an anticlockwise moment.

• Examples:

  • Using a wrench or spanner.

  • Opening a door.

  • Using a crowbar.

• Pivot points:

  • The fixed point around which rotation occurs (e.g., door hinges).

Define and calculate the moment of a force

• Moment = the turning effect of a force around a pivot.

Formula:

where:

• Moment = in newton-metres (Nm)

• Force = in newtons (N)

• Distance = in metres (m)

• Principle of moments (for balanced objects):

When an object is balanced:

• Example:

  • A see-saw is balanced if the moments on both sides are equal.

Explain how levers and gears transmit the rotational effects of forces

• Levers:

  • Levers act as force multipliers.

  • A small effort force can move a larger load if applied at the correct point.

  • They increase the moment by increasing the distance from the pivot.

• Gears:

  • Gears transmit rotational effects between shafts.

  • Large gears turn slower but with a greater force.

  • Ratios:

    • The gear ratio affects speed and force.

    • Small gear driving large gear → force increased but speed decreased (force multiplier).

    • Large gear driving small gear → speed increased but force decreased.
      

Recall that the pressure in fluids (gases and liquids) causes a net force at right angles to any surface

• Pressure in fluids:

  • Fluids (liquids and gases) exert pressure equally in all directions.

  • This pressure produces a net force at right angles (90°) to any surface.

• Examples:

  • Water pushing against the walls of a swimming pool.

  • Air pressure acting on the surface of a balloon.

Use the relationship between the force, the pressure, and the area in contact

• Formula:
  

  

  ​
  where:

  • Pressure = in pascals (Pa) (1 Pa = 1 N/m²)

  • Force = in newtons (N)

  • Area = in square metres (m²)

• Understanding:

  • A larger area reduces pressure for the same force.

  • A smaller area increases pressure for the same force.

• Hydraulic systems:

  • Work based on Pascal’s principle: pressure applied to an enclosed fluid is transmitted equally throughout.

  • In a hydraulic system:

• Small force applied on a small piston creates a larger force on a larger piston → used in car brakes and hydraulic lifts!