Moles

Key vocabulary:

Species – a molecule, atom, ion or compound in an equation.

Mole – the amount of substance. The unit is moles or mol.

Relative atomic mass – the mass found on the periodic table for an element (the mass of an atom of an element which is the weighted average mass of all the isotopes of the element, relative to 1/12 the mass of an atom of carbon-12).

Relative formula mass, M_r – the sum of all the atomic masses of atoms represented in a chemical formula.

Relative molecular mass, M_r – a term for formula mass that can be used with molecules.

Empirical formula – shows the simplest whole number ratio of the atoms of different elements present in a compound.

Relative Formula Mass, Mr (RFM):

• Ar (Relative Atomic Mass) values are used to calculate RFM.

• RFM is the sum of the Ar of all atoms in the formula.

• Relative Molecular Mass (RMM or Mr): used for molecules (e.g. CH₄).

• Relative Formula Mass (RFM or Mr): used for ionic compounds (e.g. NaCl).

• Mr is used for both molecular and ionic substances to describe relative mass.

Examples:

• Hydrogen chloride, Mr of HCl: 1 + 35.5 = 36.5

• Carbon dioxide, Mr of CO₂: 12 + (2 × 16) = 44

Calculate the Mr values of the following compounds:

1. Sodium chloride, NaCl:

   • 23 + 35.5 = 58.5

2. Potassium fluoride, KF:

   • 39 + 19 = 58

3. Sodium oxide, Na₂O:

   • (2 × 23) + 16 = 62

4. Nitrogen(IV) oxide, NO₂:

   • 14 + (2 × 16) = 46

5. Magnesium chloride, MgCl₂:

   • 24 + (2 × 35.5) = 95

6. Aluminium oxide, Al₂O₃:

   • (2 × 27) + (3 × 16) = 102

7. Phosphorus(V) oxide, P₂O₅:

   • (2 × 31) + (5 × 16) = 142

8. Copper(II) sulphate, CuSO₄:

   • 63.5 + 32 + (4 × 16) = 159.5

9. Calcium carbonate, CaCO₃:

   • 40 + 12 + (3 × 16) = 100

10. Iron(II) hydroxide, Fe(OH)₂:

    • 56 + (2 × (16 + 1)) = 90

11. Ammonium sulphate, (NH₄)₂SO₄:

    • (2 × (14 + (4 × 1))) + 32 + (4 × 16) =

    • (2 × 18) + 32 + 64 = 132

12. Lead(II) nitrate, Pb(NO₃)₂:

    • 207 + (2 × (14 + (3 × 16))) =

    • 207 + (2 × 62) = 207 + 124 = 331

Percentage Composition:

• Use Mr (atomic, molecular, or formula mass) to calculate % composition by mass.

• Formula:
  % element = (Ar of element × number of atoms / Mr of compound) × 100

Examples:

% of Cu in CuO:

• Ar(Cu) = 63.5

• Mr(CuO) = 63.5 + 16 = 79.5

• % Cu = (63.5 / 79.5) × 100 = 79.9%

% of Cu in malachite, CuCO₃·Cu(OH)₂:

• Ar(Cu) = 63.5, Ar(C) = 12, Ar(O) = 16, Ar(H) = 1

• Mr = (2 × 63.5) + 12 + (3 × 16) + (2 × (16 + 1)) =
  127 + 12 + 48 + 34 = 221

• Total Cu = 2 × 63.5 = 127

• % Cu = (127 / 221) × 100 = 57.5%

% of O in aluminium carbonate, Al₂(CO₃)₃:

• Ar(Al) = 27, Ar(C) = 12, Ar(O) = 16

• Mr = (2 × 27) + (3 × 12) + (9 × 16) =
  54 + 36 + 144 = 234

• % O = (144 / 234) × 100 = 61.5%

The % of water by mass can also be found in a compound using the same method

Examples:

% H₂O in alabaster, CaSO₄·2H₂O:

• Ar(H₂O) = 18, Mr = 172

• Water mass = 2 × 18 = 36

• % H₂O = (36 / 172) × 100 = 20.9%

% H₂O in copper(II) sulphate-5-water, CuSO₄·5H₂O:

• Ar(Cu) = 63.5, S = 32, O = 16, H₂O = 18

• Mr = 63.5 + 32 + (4 × 16) + (5 × 18) =
  63.5 + 32 + 64 + 90 = 249.5

• % H₂O = (90 / 249.5) × 100 = 36.1%

% H₂O in sodium carbonate-10-water, Na₂CO₃·10H₂O:

• Ar(Na) = 23, C = 12, O = 16, H₂O = 18

• Mr = (2 × 23) + 12 + (3 × 16) + (10 × 18) =
  46 + 12 + 48 + 180 = 286

• % H₂O = (180 / 286) × 100 = 62.9%

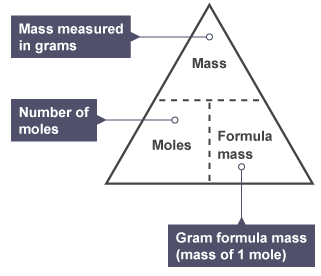
The Mole:

• The mole is a counting unit – used to measure the masses or volumes of substances in a reaction.

• Like how a dozen = 12, and a score = 20, a mole = 6 × 10²³ particles.

• One mole of any substance weighs the same as its Ar (for elements) or Mr (for compounds) in grams.

• These particles can be atoms, molecules, ions, or electrons.

• The number of particles in one mole is called Avogadro’s constant, and it is 6 × 10²³ particles/mol.

Examples:

• 1 mole of copper contains 6 × 10²³ copper atoms and has a mass of 63.5 g.

• 1 mole of carbon dioxide contains 6 × 10²³ molecules of CO₂ and has a mass of 44 g.

• 1 mole of NaCl contains 6 × 10²³ formula units of NaCl and has a mass of 58.5 g.

Number of Particles = Moles × Avogadro Constant (6 × 10²³)

Example – One mole of CO₂ contains:

• 6 × 10²³ molecules of CO₂

• 1.8 × 10²⁴ atoms total (3 atoms per molecule: 1C + 2O)

• 1.2 × 10²⁴ oxygen atoms (2 O per molecule)

Examples:

1. How many molecules are there in 3 moles of hydrogen gas (H₂)?

• Molecules = 3 × 6 × 10²³ = 1.8 × 10²⁴ molecules

2. How many hydrogen atoms are there in 3 moles of hydrogen gas (H₂)?

• Each H₂ molecule has 2 hydrogen atoms

• Atoms = 2 × 3 × 6 × 10²³ = 3.6 × 10²⁴ atoms

3. How many hydrogen atoms are there in 2 moles of ammonia (NH₃) gas?

• Each NH₃ molecule has 3 hydrogen atoms

• Atoms = 3 × 2 × 6 × 10²³ = 3.6 × 10²⁴ atoms

4. How many sodium ions are there in 10 moles of NaCl?

• 1 NaCl unit gives 1 Na⁺ ion

• Ions = 10 × 6 × 10²³ = 6.0 × 10²⁴ sodium ions

Calculating Moles from Masses:

• The moles of a substance can be found from the mass in grams and the relative formula mass.                                     

Examples of Calculating Moles:

1. Calculate the moles in 90.0 g of water (H₂O):

• Mr of H₂O = (2 × 1) + 16 = 18

• Moles = 90.0 ÷ 18 = 5.00 mol

2. How many moles are there in 102 tonnes of oxygen (O₂)?

• Convert tonnes to grams: 102 × 10⁶ = 1.02 × 10⁸ g

• Mr of O₂ = 2 × 16 = 32

• Moles = (1.02 × 10⁸) ÷ 32 = 3.19 × 10⁶ mol

3. How many moles are there in 20.6 mg of gold (Au)?

• Convert mg to g: 20.6 × 10⁻³ = 0.0206 g

• Ar of Au = 197

• Moles = 0.0206 ÷ 197 = 1.05 × 10⁻⁴ mol

Rearranging the moles formula:

The expression can also be rearranged to find either the mass or M_r of a substance.

Examples:

1. Calculate the mass of 4 moles of nitrogen (N₂):

• Mr of N₂ = 2 × 14 = 28

• Mass = 4 × 28 = 112 g

2. Calculate the mass of 2 × 10⁻³ moles of K₂O:

• Mr of K₂O = (2 × 39) + 16 = 94

• Mass = 2 × 10⁻³ × 94 = 0.188 g

3. Calculate the mass of 10 moles of calcium hydroxide (Ca(OH)₂):

• Mr = 40 + (2 × (16 + 1)) = 40 + 34 = 74

• Mass = 10 × 74 = 740 g

4. 0.02 moles of a compound has a mass of 1.64 g. Find the formula mass (Mr):

• Mr = Mass ÷ Moles = 1.64 ÷ 0.02 = 82.0 (to 3 significant figures)

Empirical Formulae:

• The empirical formula shows the simplest whole number ratio of atoms of each element in a compound.

  • Example: NaCl has a 1:1 ratio of sodium to chlorine, even though a salt crystal may be Na₅₀₀Cl₅₀₀.

• Empirical formula can be calculated using:

  • Masses of elements

  • Percentage composition by mass

  • Both are treated the same way in calculations.

Using Raw Data to Calculate an Empirical Formula:

When hydrogen is passed over an oxide of copper, it is reduced to metallic copper. Using the results obtained, calculate the formula of the oxide of copper.

Reaction:
Copper oxide + hydrogen → copper + water

• In this reaction, hydrogen reduces copper oxide to copper metal.

• The difference in mass before and after heating gives the mass of oxygen removed.

Working out the empirical formula:

Experiment to determine the empirical formula of magnesium oxide:

Safety:          

Wear a lab coat, goggles, hair tied back, tuck seats under and work standing up.

Your teacher will brief you on any additional safety measures.

Method:

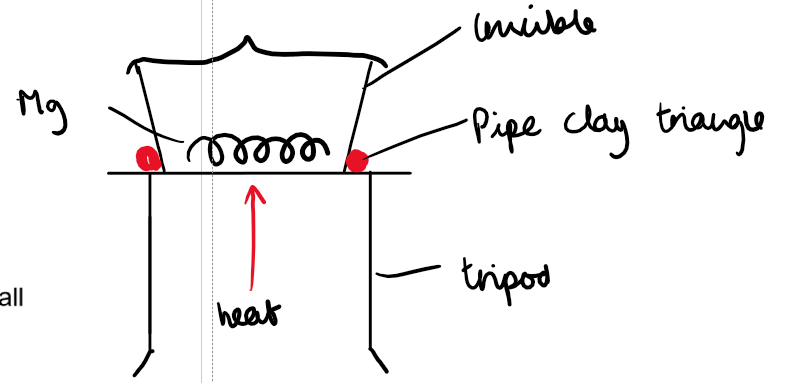
1.     Weigh a clean, dry crucible.

2.     Add a piece of magnesium ribbon (around 0.15g) and reweigh it with the lid on.

3.     Using a pipe-clay triangle and a lid, strongly heat the magnesium, lifting the lid a small amount occasionally.

4.     Reweigh the crucible and lid (making sure there is a heat mat on the balance)

5.     Repeat steps 3-4 until the mass remains constant.

Diagram:

Results:

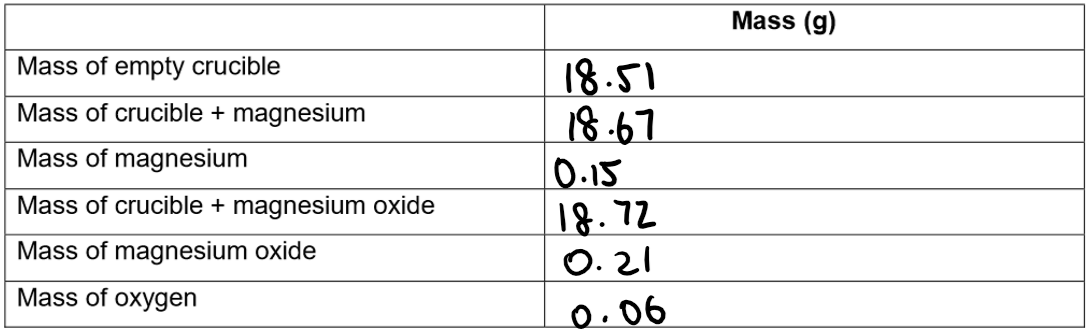
Calculation of empirical formula:

Questions:

. 1. Actual formula of magnesium oxide and explanation:

• Formula: MgO

• Explanation: Magnesium forms Mg²⁺ ions and oxygen forms O²⁻ ions. These combine in a 1:1 ratio to balance the charges.

2. Comparison with experimental formula:

• If your experimental formula differs from MgO, it means:

  • Too little oxygen: Not enough oxygen reacted due to limited air or incomplete reaction.

  • Too much oxygen: Contamination or over-oxidation led to extra mass being recorded.

3. Balanced chemical equation for the reaction:
2Mg (s) + O₂ (g) → 2MgO (s)

4. Possible sources of error and their effects:

• Not heated to constant mass or the reaction was incomplete

• Less oxygen than needed for magnesium to react, thus the final mass is lower than it should be

• Some MGO lost as smoke during the experiment

• Not weighing with the lid on consistantly

Safety:

• Wear goggles at all times.

• A safety screen or fume cupboard may be used.

Experiment overview:

Copper(II) oxide; black and copper(I) oxide; red can be reduced using methane gas.
By analysing the masses before and after the reaction, their empirical formulae can be determined.

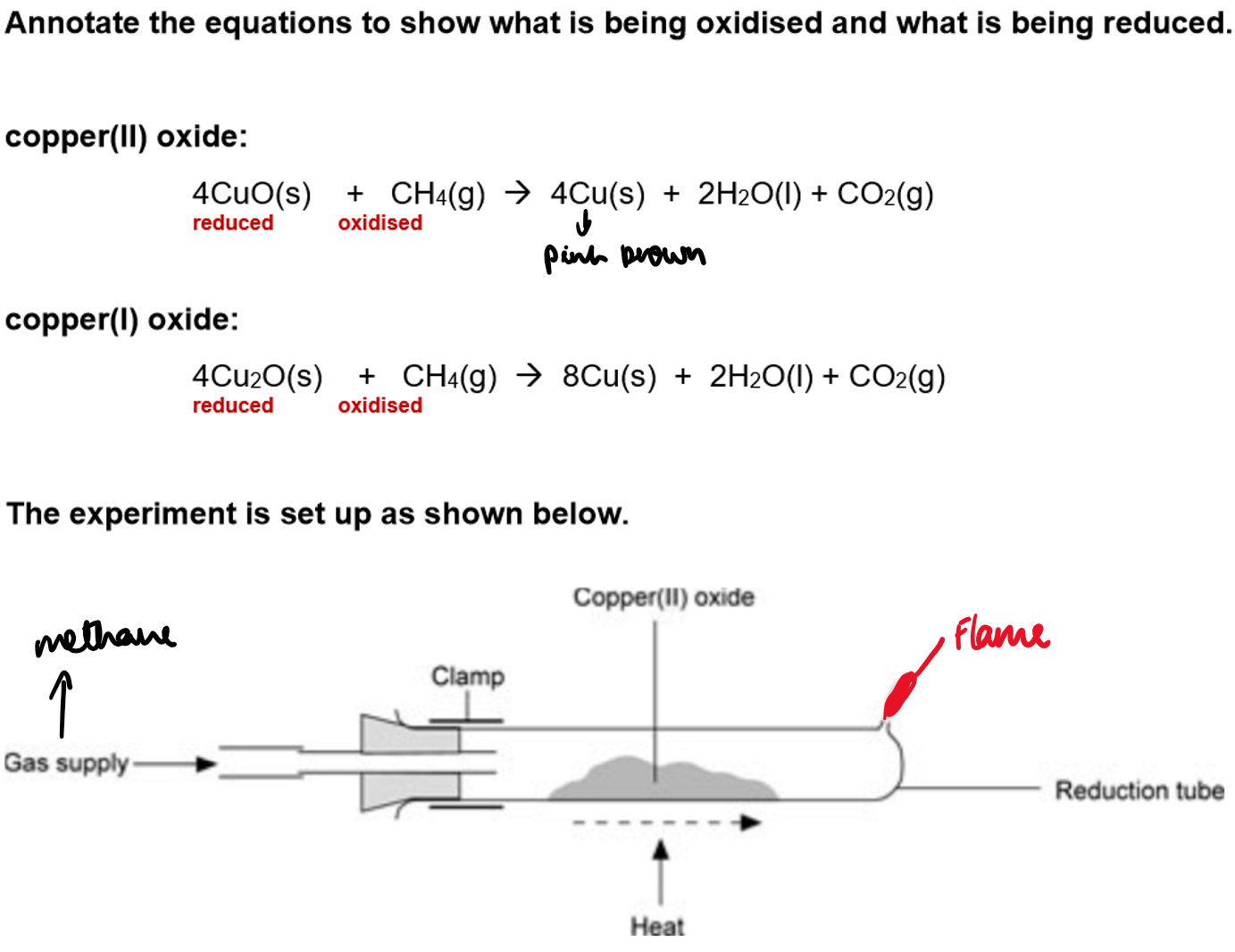
Method:

1. Weigh the empty reduction tube and record the mass.

2. Add 2 spatulas of copper oxide, weigh again, and record.

3. Turn on gas and heat with a Bunsen burner until the reaction is complete.

4. Reweigh the tube and contents, then record the mass.

5. Repeat the experiment for the other copper oxide, noting differences in reactions/results.

Results:

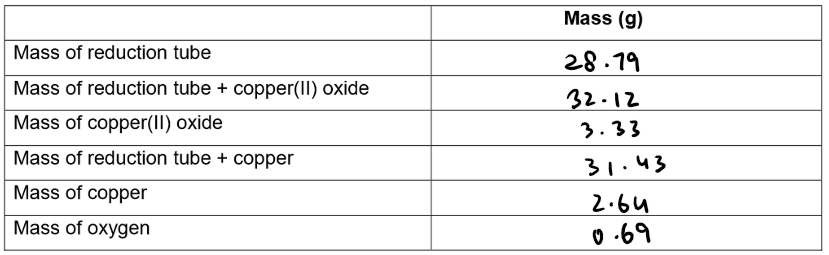
Calculation of Empirical formula:

Results:

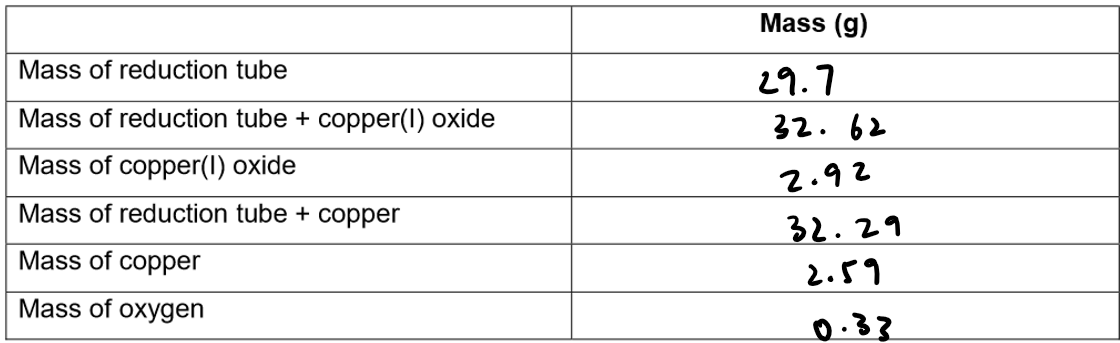
Calculation of empirical formula:

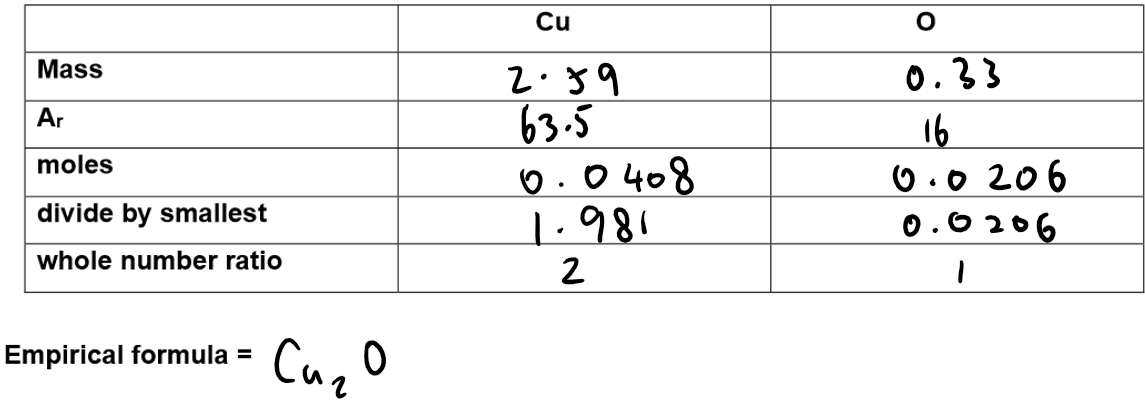
Observations and Questions

1.     What were the droplets of liquid seen at the end of the reduction tube before the apparatus became extremely hot?

Water

2.     What did each copper oxide sample look like before reduction? What did the product look like at the end?

CuO: black

Cu2O: red

After experiment, pink to brown.

3.     Why is methane passed over the product whilst it cools?

To prevent copper from reacting with oxygen in the air that gets sucked back into the tube. 

4.     How can we check that the pink/orange product is a metal?

Set up a circuit with a sample connected in series to see if the bulb lights up. 

5.     This experiment can also be carried out using hydrogen instead of methane. Write balanced chemical equations for the reduction of copper(II) and copper(I) oxide with hydrogen.

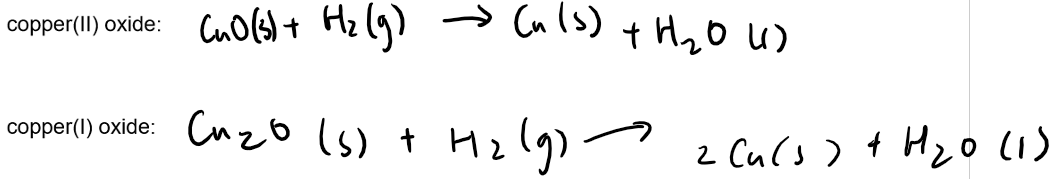
6.     Why might it be safer to carry out this experiment with methane instead of hydrogen?

Hydrogen is explosive and would require the use of safety screens

Using % composition by mass to calculate an empirical formula:

Find the empirical formula of a compound that contains 85.7% carbon with the remainder being made up of hydrogen:

Molecular formula shows the actual number of atoms of each element present in each molecule of a compound e.g. the molecular formula of butane is C₄H₁₀.

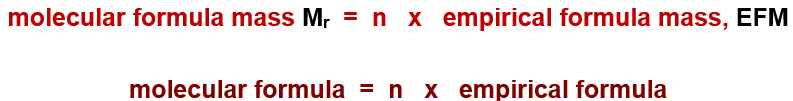
Example calculation:

Given:

• Empirical formula = CH₂

• Empirical formula mass (EFM) = 12 + (1 × 2) = 14

• Mr (Molecular mass) = 84 (given)

Steps:

1. Molecular formula = Mr / EFM
   = 84 / 14
   = 6

2. Molecular formula = 6 × (Empirical formula)
   = 6 × CH₂
   = C₆H₁₂

So, the molecular formula of the compound is C₆H₁₂.