Test 3
4.1-4.8 minus linearzation
Solving polynomomilas tips

When unable to factor you can do, sythetic division, or use the quadratic formula.
A. If you have a polynomial thats a fraction and you are setting equal to 0, rememebr that the denomunator cannot be 0 so you can just set the numerator to 0 and that will give you a X value at 0
The derivative of x is 1
Evaluate constants and variables as they can be moved around
Maxima & Minima,
Take the first derivative of the function and set it equal to 0 then solve to find the critical points.
Take the 2nd derivative of the function and input your critcal points to determince wheter that critcal point is a maximum or minimum. If the result is positive, it indicates a local minimum, while a negative result suggests a local maximum.
To find Absolute Maximum and Minimum find your critical points and input each value into the function aswell with the top and bottom values of your interval, the highest value is your max and lowest is your minimum
Inflection Points - Set the 2nd derivative equal to 0 a point of inflection is where the slope switches from increasing to decreasing.
Point of inflection is negative when slope is decresaing (Maximum)
Point of inflection is positive when clope is increasing (Minimum)
An interval in increasing from it’s starting point to it’s maximum, amd from its minimum to its endpoint.
An interval is decreasing from its maximum to it’s minimum
A function concaves upward when slope is decreasing
downward when slope is increasing
Vertical Asymptope is the denominator = 0 without numerator being 0
Relative Rates
Breakdown the givens into terms of dx/dt
then input givens and solve for the d of dt that the equation is asking for This will involve applying the chain rule to express each variable in terms of their rates of change over time, allowing us to relate them directly to one another.
Linear Approximations (Not tested)
y=mx+b
y-ynot=m(x-xnot)
L(x)=f(a)+f′(a)(x−a)
Find the slope using a value you know like root 16 instead of root 16.8856 then find the linear equation (x^1/2 in this example) and plug in the value we’re unfamiliar with (16.8856) to find slope at that point. (This is a estimate and not exact)
Differentials
Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.
dy=f’(x)dx
To compute change in y just plug in the x value into f(x), then add dx too our given x-value, compute that into f(x) and find the differnce of the 2 answers
dx = change x
dy never equals change in y
Mean Value Theorem
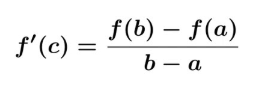
THE MVT give you Average Velocity
A point that has the same slope at the tangent line as the secant line in the equation.
When you have the slope of f’(C), take the derivative of f’(x) and o set the F’(x) = to the slope of the tangent line found and calulate the X value.
Rolles’s Therom
When the secant and tangent line has 0 slope.
Internal has to be continous, denominator can not take a value that would make it 0.
L ‘Hospitals Rule
to evaulatate a limit use f’x/g’x and then evaluatle the ;inet