Alternating Series Error Bound Theorem
The Alternating Series Error Bound Theorem is an essential concept in AP Calculus, particularly in the study of series and approximations. This theorem provides a way to estimate the error when using a partial sum to approximate the sum of an alternating series. Below is an in-depth exploration of this theorem, its applications, and related concepts.
1. Definition of an Alternating Series
An alternating series is a series where the terms alternate in sign. It is typically expressed as:

2. Convergence Conditions (Alternating Series Test)
An alternating series converges if it satisfies the following two conditions:
Monotonicity:
The terms ana_nan are monotonically decreasingex.
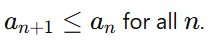
Vanishing Term Condition:
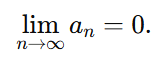
If these are satisfied, the series converges by the Alternating Series Test (Leibniz Criterion).
3. Error in Partial Sums

4. The Alternating Series Error Bound Theorem
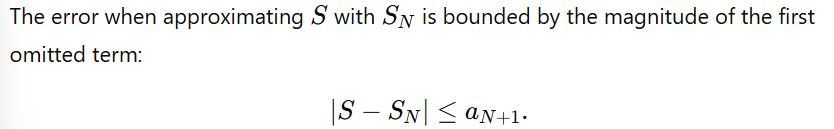
The error bound is absolute, meaning it ignores the sign of the terms.
The error is directly related to the size of the next term in the sequence, aN+1a_{N+1}aN+1.
This makes alternating series particularly useful for approximations, as the error is easy to control and calculate.
5. Examples
Example 1: Alternating Harmonic Series

Example 2: Alternating Series with Smaller Terms

6. Practical Applications
Approximating Series Sums: The error bound ensures that we can control the accuracy of approximations for alternating series.
Numerical Methods: The theorem is widely used in numerical analysis, particularly when calculating transcendental functions such as
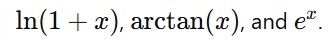
Engineering and Physics: In contexts where infinite series appear, alternating series often emerge, and the error bound ensures that approximations meet desired precision.
7. Importance in AP Calculus
Conceptual Understanding: Helps students grasp the relationship between convergence and error.
AP Exam Applications: Frequently appears in multiple-choice and free-response questions, requiring calculations and explanations of error bounds.
Connection to Taylor Series: Alternating series often connect to the error bounds of Taylor polynomial approximations.
8. Summary
The Alternating Series Error Bound Theorem is a simple yet powerful tool for approximating the sum of an alternating series. It provides a clear guideline for controlling error, making it invaluable in calculus and beyond. Its practical applications and conceptual clarity make it a cornerstone of series approximation techniques.
By understanding this theorem, students can confidently tackle problems involving alternating series and make precise approximations with minimal effort.