Geometry and Trigonometry (IB)

1. Introduction to Geometry and Trigonometry

Geometry and Trigonometry are essential branches of mathematics that deal with the properties, relationships, and measurements of shapes, angles, and distances. In the IB Mathematics curriculum, these topics form the foundation for various real-world applications, including physics, engineering, architecture, and navigation.

2. Geometry

2.1 Basic Concepts

• Point: A location in space with no dimensions.

• Line: A one-dimensional figure extending infinitely in both directions.

• Line Segment: A part of a line with two endpoints.

• Ray: A part of a line that starts at a point and extends infinitely in one direction.

• Plane: A flat, two-dimensional surface extending infinitely.

• Collinear Points: Points that lie on the same line.

• Coplanar Points: Points that lie in the same plane.

2.2 Types of Angles

• Acute Angle: Less than 90°.

• Right Angle: Exactly 90°.

• Obtuse Angle: Greater than 90° and less than 180°.

• Straight Angle: Exactly 180°.

• Reflex Angle: Greater than 180° and less than 360°.

• Complementary Angles: Two angles whose sum is 90°.

• Supplementary Angles: Two angles whose sum is 180°.

• Vertically Opposite Angles: Angles opposite each other when two lines intersect, always equal.

2.3 Properties of Triangles

• Sum of Interior Angles: 180°.

• Pythagorean Theorem: In a right-angled triangle, where and are the legs, and is the hypotenuse.

• Congruent Triangles: Triangles with equal corresponding sides and angles (SSS, SAS, ASA, RHS).

• Similar Triangles: Triangles with equal corresponding angles and proportional sides (AA, SAS, SSS).

• Isosceles Triangle: A triangle with at least two equal sides.

• Equilateral Triangle: A triangle with all sides and angles equal.

• Scalene Triangle: A triangle with all sides of different lengths.

• Right-Angled Triangle: A triangle with one 90° angle.

2.4 Quadrilaterals and Polygons

• Sum of Interior Angles of a Polygon: , where is the number of sides.

• Regular Polygons: All sides and angles are equal.

• Properties of Quadrilaterals:

  • Parallelogram: Opposite sides are equal and parallel.

  • Rectangle: Opposite sides are equal, and all angles are 90°.

  • Rhombus: All sides are equal, opposite angles are equal.

  • Square: A rectangle with all sides equal.

  • Trapezium: One pair of parallel sides.

  • Kite: A quadrilateral with two pairs of adjacent sides equal.

2.5 Circles

• Circumference:

• Area:

• Chord, Arc, Sector, Segment: Various parts of a circle.

• Circle Theorems: Key properties related to angles, tangents, and chords.

• Tangent Properties: A tangent to a circle is perpendicular to the radius at the point of contact.

3. Trigonometry

3.1 Trigonometric Ratios

For a right-angled triangle:

3.2 Special Angles

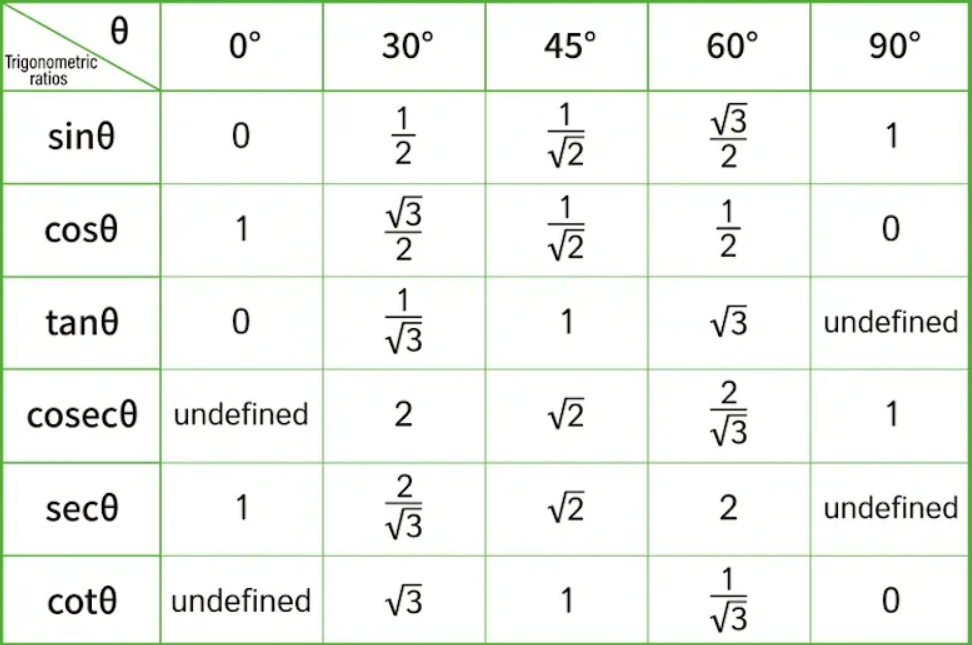
3.3 Trigonometric Identities

3.4 The Sine and Cosine Rules

For any triangle:

• Sine Rule:

• Cosine Rule:

3.5 Applications of Trigonometry

• Angles of Elevation and Depression

• Navigation and Bearings

• Physics Applications (e.g., wave motion, oscillations)

• Construction and Architecture

• Astronomy: Calculating distances of celestial bodies

• Computer Graphics: Used in transformations and animations