INTRODUCTION TO PHYSICS (7)

• One of the basic goals of physics is to investigate energy, particularly, about effectively and efficiently obtaining, using, and conserving energy.

ENERGY

• Energy is a scalar quantity associated with a body and/or a system.

• The main basis of energy is based on the principle of conservation of energy which states that energy cannot be created or destroyed, just be changed from one form to another.

• One type of energy is kinetic energy and the way in which it can be transferred is work.

KINETIC ENERGY

• Kinetic energy K is the energy that an object possesses due to its motion.

• The kinetic energy of an object is 0 when the object is at rest.

• For an object with a mass m and speed v which is well below the speed of light, kinetic energy can be calculated by the equation:

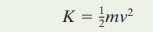
• The SI unit of energy is Joules (J) and has the base unit of kg(m/s)^2.

WORK

• When force is applied to increase the speed of an object, the kinetic energy of the object increases.

• Similarly, a force can be applied to slow down an object, and therefore, decrease its kinetic energy.

• These changes are referred to as the energy being transferred to or gained from the object. This is said to be the work done on the object by the force.

• By definition, Work W is energy transferred to or from an object by means of a force acting on the object.

• Energy transferred to the object is positive work, and energy transferred from the object is negative work.

• Work is a scalar quantity and has the same unit as energy, i.e. Joules.

• The ‘transfer’ of energy should not be confused with the transfer of matter.

• Work can be calculated by multiplying the force applied by the distance traveled in the direction of the applied force.

• To calculate the work done by a constant force, the force and distance are further multiplied by the cosine value of the angle between the directions of force and displacement.

• To use the equation above, it is to be ensured that the force applied is constant, and the object must be particle-like, i.e. all parts of the object should move at together in the same direction.

• Work done can be either positive or negative.

• A force does positive work when it has a vector component in the same direction as the displacement, and it does negative work when it has a vector component in the opposite direction. It does zero work when it has no such vector component.

• When two or more forces act on an object, the net work is the sum of work done by all individual forces.

• Net work can be calculated in two ways: either the work done by all the forces is calculated individually and then summed up together, or the net (resultant) force is calculated and used in the formula.

• Work and kinetic energy can also be related to each other as shown below:

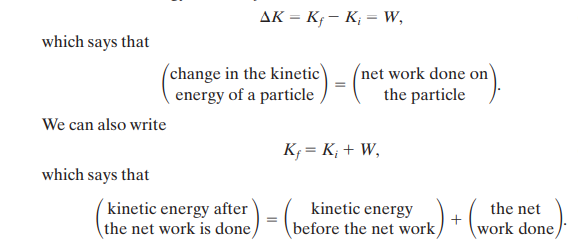This is generally known as the work-kinetic energy theorem.

WORK DONE BY THE GRAVITATIONAL FIELD

• Work done by the gravitational field strength is given by:

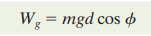  where m is the mass, g is the gravitational field strength, d is the displacement during which the work is done, and theta is the angle between the directions of force and displacement.

WORK DONE IN LIFTING AND LOWERING OBJECTS

• When an object is lifted, the force applied upward to it does the positive work while the force of gravity does the negative work, i.e. the applied force transfers energy to the object being lifted while gravitational energy takes away the energy from the object.

• Therefore, the net change in kinetic energy of the object is the sum of the work done by both the forces (since the work by gravitational energy is negative, it is actually subtracted).

• The same principles above are applied when the object is lowered, however, then the applied force takes energy from the object being lowered while gravitational energy transfers the energy to the object.

• If the initial and final kinetic energies are equal (or 0), the work done by the force applied and the gravitational force are equal in magnitude but opposite in direction.

WORK DONE BY SPRING FORCE

• Many forces in nature have the same mathematical form as the spring force so by gaining an understanding of this force, a lot of other forces will also be explained.

• When a spring is stretched or compressed, it pulls back to return to its original relaxed state.

• Since a spring force acts to restore the relaxed state, it is sometimes called the restoring force.

• According to a near estimate, the force F from the spring is proportional to its displacement d of the free end from its position when the spring is in the relaxed state. Therefore, the spring force is given by F= -kd where k is the spring/force constant, the measure of a spring’s stiffness.

• The larger the value of k, the harder it is to stretch a spring. SI unit of the spring constant is Newton per metre.

• The minus sign is because the direction of the spring force and its displacement from the free end is always opposite to one another.

• The equation above (F=-kd) is called Hooke’s law, after the scientist Robert Hooke.

• If an object is attached to a string and given a little jerk, its work done cannot be calculated by the equation (W = Fd cos theta) because there is no one value of F to put into that equation—the value of F increases as the block stretches the spring.

• Therefore, we follow three steps to overcome this problem and find the work done by the spring force:

  1) Divide the object’s displacement into small segments so the variation of force F in each segment is not very significant.

  2) Use the value of F in the equation (W = Fd cos theta) to find the work done in each section.

  3) Add the values of each segment’s work to find the total work.

• However, this is a lengthy process, and integration can be used to make this more efficient.

The net work Ws done by the spring, from xi to xf, is the sum of all these works:

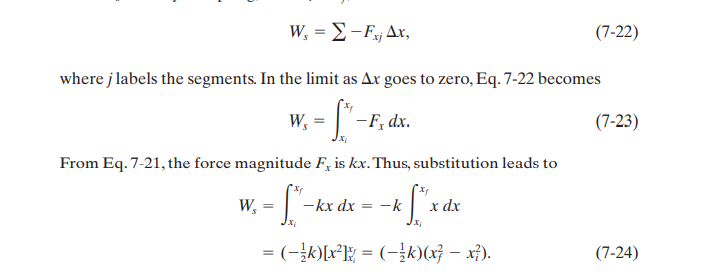
By multiplying, we get the final result:

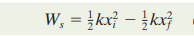
• Work Ws is positive if the block ends up closer to the relaxed position (x = 0) than it was initially. It is negative if the block ends up farther away from x = 0. It is zero if the block ends up at the same distance from x = 0.

• If the block that is attached to a spring is stationary before and after a displacement, then the work done on it by the applied force displacing it is the negative of the work done on it by the spring force.

• It is important to note that in the above experiments, we assumed the spring to be massless and ideal (that is follows the Hookes Law), the object to be particle-like, and the contacts to be frictionless.

WORK DONE BY A GENERAL VARIABLE FORCE

POWER

• Power is the rate at which work is done.

• Power due to a force is calculated by the total work done upon the change in time.

• Instantaneous power is the instantaneous time rate of doing work which can be calculated by taking the derivative of work done with respect to time.

• SI unit of power is joules/second. This unit is commonly known as the Watt, denoted by the capital letter W.

• Horsepower, also often used, is equal to 746W.

• By using the formula of power (WD/t) it is observed that work can also be defined as the product of power and time, which is the common kilowatt hour.

• If we want to express power in terms of velocity, it can be written as the product of the applied force and the velocity of the object.