Chapter 10- Rotation

INTRODUCTION TO PHYSICS (10)

• We know that physics is used to study and analyse motion. However, until now we have just observed translation.
• Translation is the motion of the body when it moves along a straight or curved path.
• Rotation, which will be discussed now, is when a body turns along an axis.

Rotation has applications ranging from less serious matters such as hitting a golf ball to more serious matters such as metal parts in airplanes.

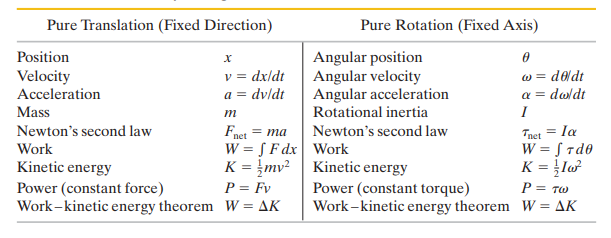
ROTATIONAL VARIABLES

• A rigid body is a body that has all its parts locked together and keeps its shape during rotation.
• A fixed axis is an axis that does not move.
• We shall first observe the rotation of a rigid body around a fixed axis. Therefore, we are not discussing examples such as that of the sun or a bowling ball.
• The axis around which rotation occurs is known as the axis of rotation or the rotation axis.
• In pure rotation which is also known as angular motion, every point of the body moves in a circle whose center lies on the rotational axis, and every point moves through the same angle in that particular time interval.
• You already know about terms such as displacement, velocity and acceleration in linear motion (translation). These terms also have their angular equivalents.

ANGULAR POSITION

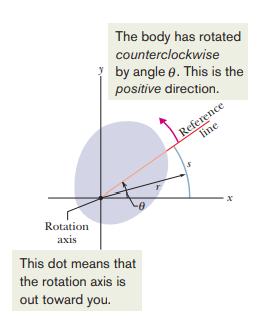
• In the diagram above, the reference line is a line perpendicular to the rotation axis, and rotating with the body.
• The angle of this reference line to a fixed position is called the angular position, and the fixed position about which the angular position is taken is known as the zero angular position.
• In the diagram above, the positive x-axis is the zero angular position, and therefore, the angular position theta is measured relative to it.
• We know that theta can be given be the expression s/r where s is the arc length that extends from the zero angular position (the positive x-axis in this case) to the reference line, and r is the radius of he circle that rotation makes.
• The angle in this is measured in radians which is a pure number with no dimension.
• There are 2π radians in a complete circle, and 1 rad is equal to 57.3 degrees.
• It is important to remember that the angle theta is not reset when the reference line crosses the zero angular position. In the diagram above, if the reference line completes two full circles, he angle will become 4π.

ANGULAR DISPLACEMENT

• Imagine that the body in the diagram above rotates a little more to change its angular position from theta1 to theta2. The body is then said to undergo angular displacement Δθ, given by:

  

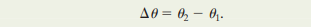
• This definition holds for every particle in the body and also for thee body as a whole.

• Similar to linear displacement which also has a positive and a negative direction, angular displacement is also a vector quantity with a direction.

• An angular displacement in the counterclockwise direction is positive, and one in the clockwise direction is negative.

ANGULAR VELOCITY

• If we say that our rotating body is at θ1 at t1 and θ2 at t2, the average velocity of the body is given by:

  

  

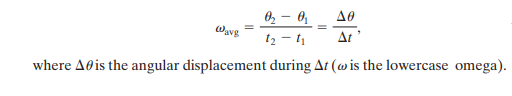
• Instantaneous angular velocity is the limit of ratio as time approaches zero which is given by:

• 

• The unit of angular velocity is radian per second (rad/s) or revolutions per second (rev/s).

• The direction of angular velocity is either positive or negative. It is positive when it travels anticlockwise and negative when it travels clockwise.

• The magnitude of angular velocity is the angular speed also represented by ω.

\

ANGULAR ACCELERATION

• If angular velocity is not constant, the body is said to be undergoing angular acceleration.

• The average angular acceleration is given by the change in velocity over change in time.

  

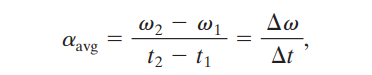
The instantaneous angular acceleration is when time approaches zero. It is given by:

The unit of angular acceleration is commonly the radian per second-squared (rad/s^2 ) or the revolution per second-squared (rev/s^2 ).

\

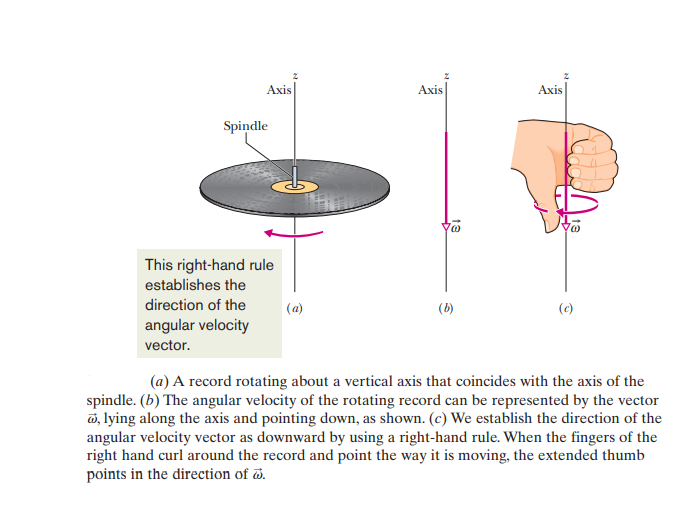
ANGULAR VELOCITIES AS VECTORS

• We use vectors to tell the direction of a moving object. When there are only two directions available, e.g. for a particle moving in a straight horizontal line, the direction is represented by a plus/minus sign.

• For angular rotations, there are two directions as well: the clockwise and the anticlockwise directions which are denoted by the plus/minus signs. However, angular rotations can be treated as vectors as well.

• It is very important to remember that while angular velocities can be represented as vectors, angular displacements cannot since they do not pass the vector addition test.

  

ROTATIONS WITH CONSTANT ANGULAR ACCELERATION

• We know that the main equations of motion are when there is constant linear acceleration in a linear motion.

• Similarly, there are angular motion equivalents of these equations which are used when there is a constant angular acceleration.

• When a rigid body rotates, all the particles complete one revolution in the same time, with the same angular momentum, w.

• The linear speed of each particle depends on its position from the centre, i.e. the circumference. The more the circumference, the greater the linear speed w. It is to be noted that the angular speed does not noticeably change.

• Linear variables and rotational variables are related by the perpendicular distance from the body and its rotational axis, denoted by r.

• To find the distance, s of a body along the circular axis, the angle theta at which the body is rotating is multiplied by r.

  

• To calculate linear velocity, the angular speed w is multiplied by r.

  

• To find the time of one revolution:

  

or

• To find the acceleration of the body

  

\

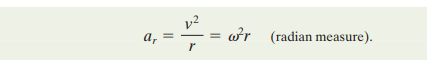
KINETIC ENERGY OF ROTATION

• In rotating bodies, we cannot use the formula K.E= 1/2 x m x v^2 since that would only give the kinetic energy of the centre of mass of the object which is 0.

• Instead, the kinetic energy of a rotating body can be calculated by adding all the energies of its many particles (consider the rigid body as made up of a number of particles that are moving at different speeds.)

• Therefore, we get the formula:

  

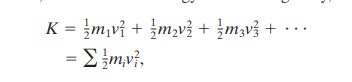
• However, since the velocity of all the particles is different, we replace v with wr. This gives us:

  

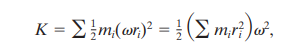
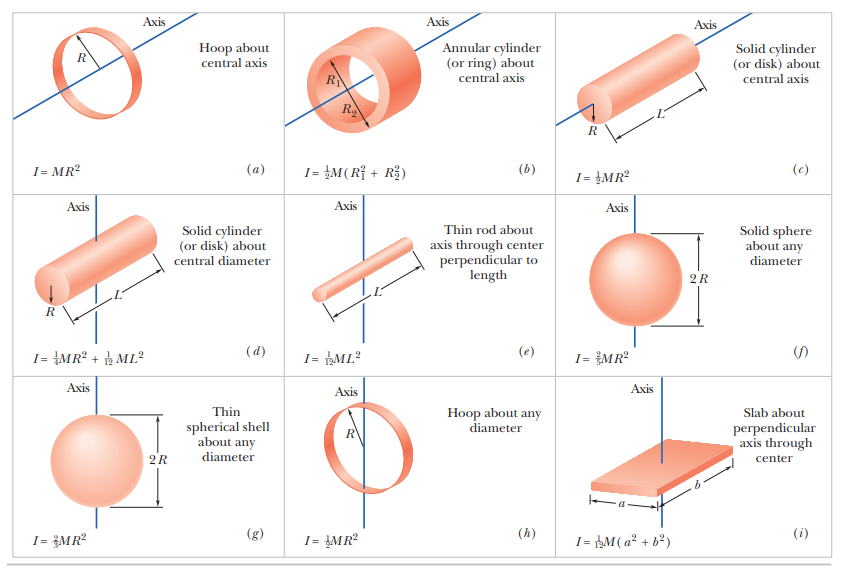
ROTATIONAL INERTIA

To calculate rotational inertia, we use the following formula:

• A theorem called parallel axis theorem is used to finding the moment of inertia of the area of a rigid body whose axis is parallel to the axis of the known moment body.

• It is explained in the diagram below:

  

\

TORQUE

• To rotate any body, force is applied. The force applied has two components.
• One component called radial component passes through the rotating point (pivot) and therefore, produces no moment.
• The other component called tangential component is however, perpendicular, and creates a moment about the pivot.
• This component is calculated by Fsin(theta) where F is the total force applied.
• Moment also depends on the perpendicular distance from the pivot. Therefore, these two factors are incorporated into the formula for calculating moment:

\

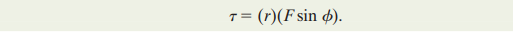
• It is important to remember that when several torques act on a body, the net torque is equal to the sum of all the individual torques.

\

WORK AND KINETIC ENERGY

• Work and kinetic energy are related by the kinetic energy-work theorem stated below:

  

• For motion along the x-axis, work can be calculated by:

  

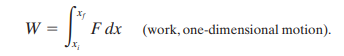
• This can be reduced to W=Fd where F is the force and d is thee displacement in the direction of the force. Power is the rate of work done, i.e. the derivative of work against time.

• The situation for the rotational body is similar. As it rotates, the force does work which can change the kinetic energy.

• Suppose that only the energy of the body changes, thus, work and kinetic energy can still be related by the theorem:

  

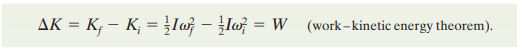
CORRESPONDING RELATION FOR TRANSLATION AND ROTATIONAL MOTION

\