Newton's Third Law of Motion

5.1

Forces and Interactions:

• Every force is part of an interaction between two objects.
• For each interactions, the forces are equal in magnitude and opposite in direction.
• Consider a boxer:
  • When their fist hits a punching bag, they dent the bag, and the bag stops their fist from moving further.
  • If their fist were to hit a tissue, they wouldn’t be able to exert the same force as they did on the punching bag, as the tissue wouldn’t exert the same force back.
• For any interaction, there need to be two forces, and they need to be acting on separate objects.
• The forces make up a singular interaction, and the objects in the interaction need to be treated equally.
• One force is not the ‘exerter’ while the other is the ‘receiver’.

5.2

Newton’s Third Law of Motion:

• Statement:

When one object exerts a force on a second object, the second object exerts an equal and opposite force on the first.

• One force is the action force.
• The other force is the reaction force.
• To every reaction, there is always an opposed equal reaction.
• Neither force exists without the other.
• The reaction force accounts for motion and depends on friction.
• Forces exist in force pairs.

\

Defining Your System:

• The action and reaction forces don’t always cancel to zero. Here’s why:

  Consider two objects, A and B.

  • Case 1: A forms a system.
  • Case 2: A and B are two individual systems.
  • Case 3: A and B form one signal.

  

• Case 1: The arrow pointing away from A represents an external force on the system.

• Case 2: A exerts a force on B that may or may not affect B, but doesn’t affect A. Similarly, B exerts a force back. The action and reaction forces don’t cancel out.

• Case 3: A and B exert forces that form a force pair. These forces are within and the same system, and cancel out. They do not accelerate the system.

  • Another external force is needed for the system to accelerate. This force is friction.
  • When B pushes against the floor, the floor pushes back, and causes the system to accelerate.

• Another example: All the interatomic forces holding a football together form action-reaction pairs, but they don’t accelerate the football.

• Two opposing kicks on the football, however, would not form an action reaction pair because they’re acting on the same object, not on different objects.

5.3

Action and Reaction on Different Masses:

• When an object falls, it’s pulled towards the Earth, and it pulls the Earth towards itself.
• Earth accelerates slightly when an object falls towards it.
• For two bodies A and B, the acceleration of A towards B is:
  • equal to the acceleration of B towards A when both of them have the same mass.
  • less noticeable when A’s mass is larger than B’s.
  • more noticeable when A’s mass is lesser than B’s.

\

• A fired cannon gives us better evidence of the difference in mass.
  • When the cannon is launched from a cannonball, a pair of forces acts between the two.
  • Although the forces are equal in magnitude, the cannon doesn’t recoil with the same speed as the cannonball, since it’s heavier.

\

• By Newton’s second law, acceleration also depends on mass.
  • Acceleration is inversely proportional to mass.

\

• Common misconception → Rockets are propelled by exhaust gases from the atmosphere.
• Truth → Rockets are propelled by the reaction forces exerted by the material fired out of them.
  • Rockets actually operate better above the atmosphere because there’s no air resistance.

\

• The whirling blades of a helicopter force air particles down → Action force.
• There is an upward reaction force called lift → Reaction force.

\

5.4

Vectors and the Third Law:

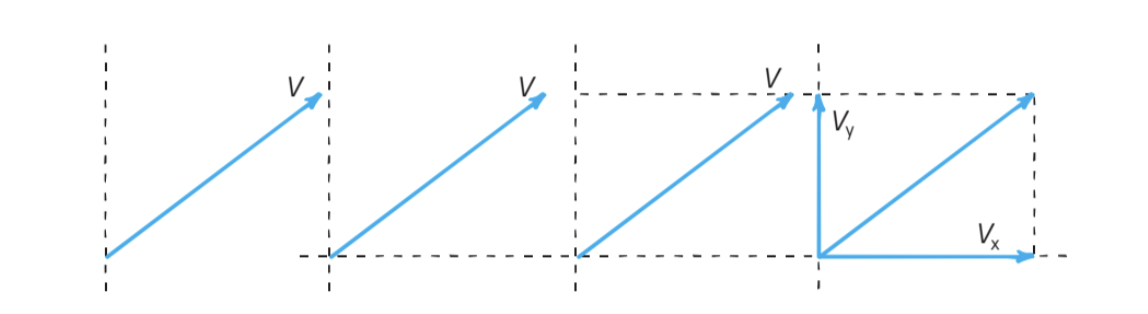
• Two vectors at right angles can be resolved into one.

• One vector can be split into two parts perpendicular to each other.

• These parts are called components.

• Resolution → The process of splitting a vector into its components.

• The components are horizontal and vertical.

• An illustration of vector resolution:

  

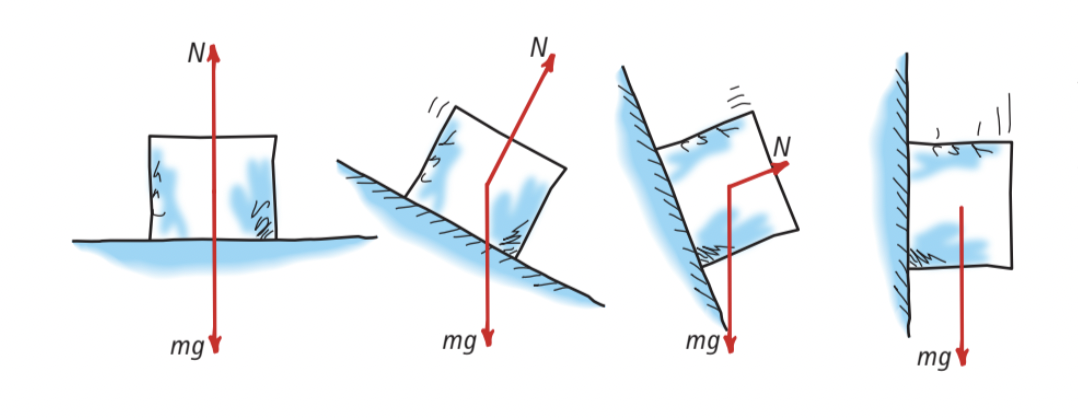
• For an object on a horizontal surface, it exerts its weight (mg) downwards, perpendicular to the surface.

• For an object on an inclined surface, its weight (mg) is still exerted downwards, but it is no longer perpendicular to the surface.

  

• Consider a monkey pulling down diagonally on a rope.

• \

  

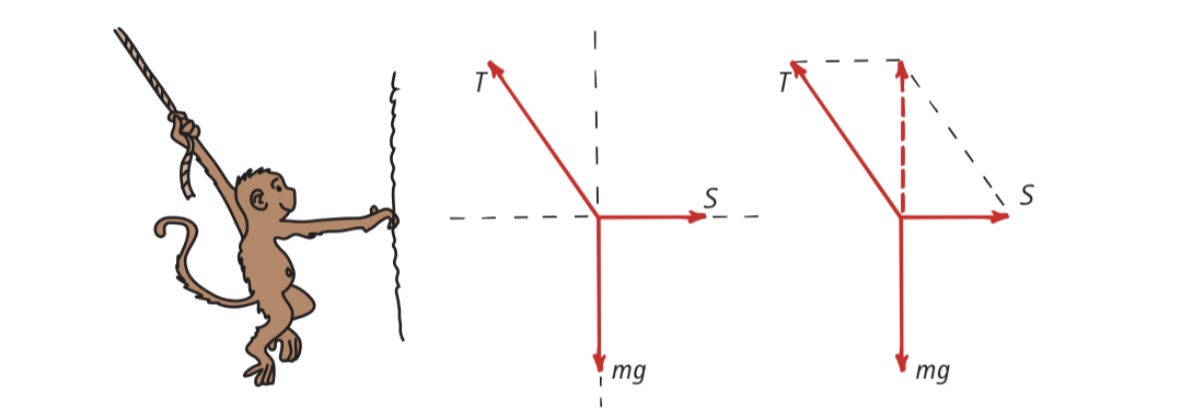
• It pulls down with a tension T.

• This tension gets split into S and mg.

  • S → sideways pull on the rope.
  • mg → weight of the monkey acting vertically downwards.

• Here, S is the horizontal component of the vector T, and mg is the vertical component.

\

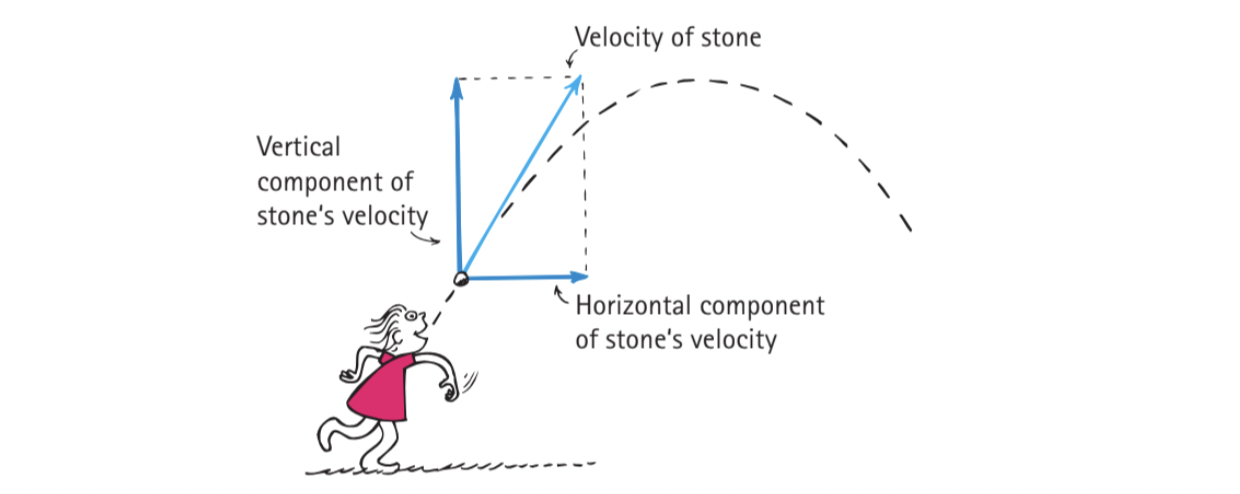
• Consider a stone being thrown:

  

5.5

Summary of Newton’s Three Laws:

• Law 1 → An object at rest tends to stay at rest, and an object in motion at a constant speed along a straight line path tends to stay in motion.
• This property of resisting changes in motion is called inertia.
• Objects undergo changes in motion when a net force not equal to zero acts on them.

\

• Law 2 → When a net force acts on an object, the object accelerates.
• This acceleration is:
  • directly proportional to the force acting on the object.
  • inversely proportional to the mass of the object.
  • in the direction of the force acting on the object.
• a = F/m
• For an object falling in a vacuum, net force = pull of gravity. (g)
  • g = acceleration due to gravity
• For an object falling in air, net force = force of gravity - force of air resistance.
  • When air resistance = gravitational force, acceleration = 0
  • In this state, the object falls at a constant speed called terminal speed.

\

• Law 3 → When one object exerts a force on another, the second object exerts an equal and opposite force on the first.
• Forces occur in pairs.
  • One force is the action force.
  • The other is the reaction force.
  • These two forces constitute the interaction between two objects.
• Action and reaction always occur simultaneously on an object.

\
Newton’s three laws are the rules of nature that connect everything around us together.

\