Quantum & Nuclear Physics
12.1 Interaction of Matter with Light
Photons and Light
Light is composed of particles called photons.
Each photon has an energy given by E=hf, planck's constant(h)*frequency of wave
Photons also have momentum, described by p=𝜆h
The Photoelectric Effect
Occurs when light ejects electrons from a material's surface, provided the light's frequency is above a certain threshold.
Observations include:
Intensity of light does not affect the energy of emitted electrons.
Emitted electron energy is directly proportional to the light frequency.
Below a minimum frequency, no electrons are emitted, regardless of light intensity.
Electron emission occurs without any noticeable delay.
Einstein’s Explanation of the Photoelectric Effect
Proposed that light consists of photons with quantized energy.
A photon's energy must exceed the material's work function.
The maximum kinetic energy () of an emitted electron is given by =hf-
The stopping voltage in a photoelectric experiment is related to the maximum kinetic energy of the photoelectrons by eV=hf-, where e is the charge of the electron, and V is the stopping potential
is the stopping potential.
Matter Waves
Proposed by de Broglie, suggesting particles such as electrons exhibit wave properties, with a wavelength.
Pair Annihilation and Pair Production
Pair Annihilation: A particle and its antiparticle annihilate to produce photons.
Pair Production: A photon creates a particle-antiparticle pair, requiring the presence of a nucleus to conserve momentum and energy.
Quantization of Angular Momentum
Bohr's model suggests that angular momentum of an orbiting electron is quantized,

Where n is the shell level
Leads to discrete or quantized energy levels within the atom, which is calculated using the following formula:
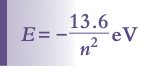
The Wave Function
A mathematical function describing the quantum state of a particle.
The square of its amplitude represents the probability density of finding a particle in space.
The Uncertainty Principle
Stated by Heisenberg, it asserts a fundamental limit to the precision with which pairs of physical properties, like position(x), and momentum (p), given by

The Electron in a Box (Particle in a One-Dimensional Box Model)
Demonstrates quantization of energy levels; an electron confined in a 'box' can only occupy certain energy states. illustrates quantum mechanical properties such as discrete energy levels and the wave nature of particles.
Quantum Tunneling
A phenomenon where particles can pass through a potential barrier, even if they do not possess enough energy to overcome the barrier classically. Has significant implications for nuclear fusion, semiconductor devices, and various other quantum phenomena.
12.2 Nuclear Physics
Rutherford Scattering
Rutherford's gold foil experiment: Alpha particles are scattered by a thin gold foil, leading to the discovery of the dense, positively charged nucleus.
Scattering formula: Scattering angle distributions can be predicted, but the formula for distance of closest approach
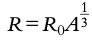
**NOTE: ALL NUCLEI HAVE THE SAME DENSITY: 
Distance of Closest Approach
Represents the nearest point an alpha particle comes to the nucleus during scattering, determined by the particle's kinetic energy and the electric charge of the nucleus.
Deviations from Rutherford Scattering
At very close distances, alpha particles deviate from the expected path, hinting at nuclear forces and the structure of the nucleus.
Nuclear Energy Levels
Similar to electrons in atoms, nucleons (protons and neutrons) within the nucleus also have quantized energy levels.
Transitions between these levels can emit or absorb gamma rays, analogous to the photon emissions or absorptions in atomic transitions.
The Neutrino
Hypothesized to account for the conservation of energy, momentum, and angular momentum in beta decay.
A nearly massless and chargeless particle, it interacts with matter only through the weak nuclear force.
Radioactive Decay Law
The rate of decay of a radioactive isotope is described by
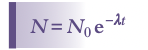
![]()

Where A is the activity, that is the number of nuclei decaying per second, lambda is the decay constant which is the probability a nucleus decays in a second. The decay constant multiplied by number of nuclei is the activity.
Minimum Formula
We know from diffraction that if the de Broglie wavelength λ of the electrons or neutrons is about the same as that of the nuclear diameter, the electrons and neutrons will diffract around the nuclei.A minimum will be formed at an angle θ to the original direction according to:
