Math 119: Mathematics for Elementary School Teachers

this shouldn’t be used as a substitute for going to class btw :p

Polya’s Problem Solving Four Steps

1. Understanding the Problem
2. Devising a Plan
3. Carrying Out the Plan
4. Looking Back

Five Problem-Solving Strategies

1. Making a Drawing
2. Guessing and Checking
3. Making a Table
4. Finding a Pattern

Geometric Sequence

Each new number is obtained by multiplying the previous number by a common ratio

a) 5, 25, 125… Next term: (==625==), The type of sequence: ==geometric==

• the common ratio here is ==5==
  • 5 x 5 = 25, 25 x 5 = 125, etc.

b) 1, 6, 36, 216… Next term: (==1296==), The type of sequence: ==geometric==

• the common ratio here is ==6==
  • 1 x 6 = 6, 6 x 6 = 36, 36 x 6 = 216, etc.

Arithmetic Sequence

Each new number is obtained from the previous number in the sequence by adding a common difference

a) 5, 10, 15… Next term: (==20==), The type of sequence: ==arithmetic==

• the common difference here is ==5==
  • 5 + 5 = 10, 10 + 5 = 15, 15 + 5 = 20

b) 9, 18, 27… Next term: (==36==), The type of sequence: ==arithmetic==

• the common difference here is ==9==
  • 9 + 9 = 18, 18 + 9 = 27, 27 + 9 = 36

Finite Differences

A method approaching number patterns can be found by looking at the differences between consecutive terms

a) 0, 3, 8, 15, 24

• the difference between each number increases by ==2==
  • 3 - 0 = 3, 8 - 3 = 5, 15 - 8 = 7, 24 - 15 = 9
• using this, we can find the next number in the chain
  • 9 + 2 = 11, 24 + 11 = 35, so the next number is ==35==

b) 1, 4, 9, 16, 25

• the difference between each number increases by ==2==
  • 4 - 1 = 3, 9 - 4 = 5, 16 - 9 = 7, 25 - 16 = 9
• using this, we can find the next number in the chain
  • add two to nine, 9 + 2 = 11, then add the sum to the last number in the sequence (25), 25 + 11 = ==36==

Fibonacci Numbers

After the first two sequence of numbers, each successive number can be obtained by adding the previous two numbers

a) 1, 1, 2, 3, 5, 8… The next term is (?)

• add the first two numbers, 1 + 1= 2, then the sum by the previous number, 2 + 1 = 3, and continue
  • 3 + 2 = 5, 5 + 3 = 8, 8 + 5 = 13
  • therefore, our next term is ==13==

Inductive Reasoning

The process of forming conclusions on the basis of patterns and observations, also called an ==informed guess==

a) Mary has two eyes

Max has two eyes

Mason has two eyes

Mary, Max and Mason are human beings

Therefore, human beings have two eyes.

• the pattern here is that all the people have two eyes, and since they are all humans, it can be inferred that all humans have two eyes

b) 1 + 2 + 3 = 6

2 + 3 + 4 = 9

3 + 4 + 5 = 12

4 + 5 + 6 = ?

• the pattern here is that each sum increasing by 3
• therefore, we can infer that the final sum will also increase by 3
  • 12 + 3 = 15
• we should check our answer, though, just to make sure it’s correct
  • 4 + 5 = 9, 9 + 6 = 15

Deductive Reasoning

The process of forming conclusions on the basis of logic, or reasoning from one or more statements to reach a logical conclusion

Has three components

• ==Logic== is the science that evaluates the argument, which is a group of statements including one or more premises and one and only one conclusion (or a statement that is either true or false)
• ==Premise== is a statement that provides reason or support for the conclusion
• ==Conclusion== is a statement in an argument that convinces the audience

a) Given Statements (or Premises)

1. The sum of two numbers is 24
2. One of the numbers is 10

• Given this information, we can subtract 10 from 24 and find the conclusion
  • 24 - 10 = 14

Conclusion

The other number is 14.

Venn Diagrams and Deductive Reasoning

Venn diagrams are used to representing information, and using deductive reasoning with these diagrams can help us draw conclusions

a) Premises

1. All students in room 210 are taking English 441
2. All students who are taking English 441 are students at Queens College

Conclusion

Therefore, all students in room 210 are students at Queens College

• now, to represent this in a diagram

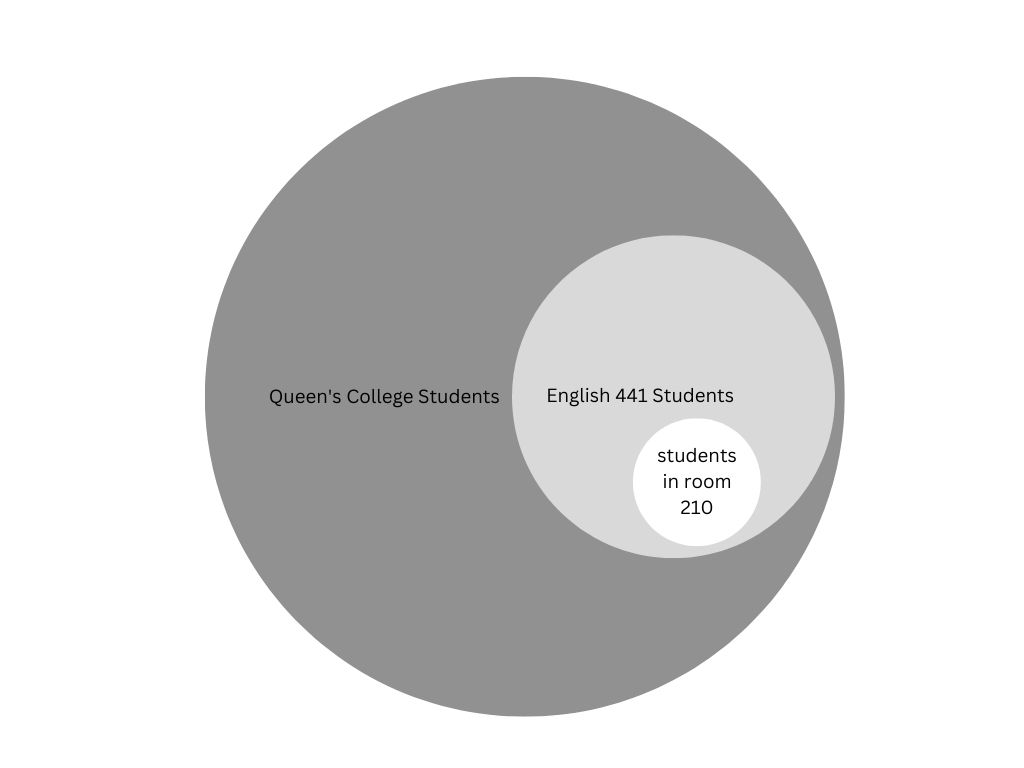  b) Premises

1. All orcas are whales
2. All whales are mammals

Conclusion

All orcas are mammals

Law of Detachment

When a conditional statement is given (premise 1), and the if part is satisfied (premise 2), the then part will logically follow

Premises

1. If p, then q
2. p

Conclusion

q (valid)

a) Premises

1. If the temperature is below 32F, then water will freeze.
2. The temperature is below 32F today.

Conclusion

Water will freeze.

b) Premises

1. If the trip is over 300 miles, the campers will run out of fuel.
2. The campers ran out of fuel.

Conclusion

The trip was over 300 miles.

Law of Contraposition

When a conditional statement is given (premise 1) and the negation of the then part is given (premise 2), the negation of the if part will logically follow

Premises

1. If p, then q
2. Not q

Conclusion

Not p (valid)

a) Premises

1. If the temperature is below 32F, then water will freeze.
2. The temperature is not below 32F today.

Conclusion

Water will not freeze.

b) Premises

1. If the trip is over 300 miles, the campers will run out of fuel.
2. The campers did not run out of fuel.

Conclusion

The trip was not over 300 miles.

Conditional Statement Forms

Conditional Statement

• If p, then q.
  • If a person lives in NY, then the person lives in the United States

Converse

• If q, then p.
  • If a person lives in the United States, then the person lives in NY
• the converse is not always true

Inverse

• If not p, the not q.
  • If the person does not live in NY, then they do not live in the United States
  • the inverse is not always true

Contrapositive

• If not q, then not p.
  • If the person does not live in the United States, then they do not live in NY
• the contrapositive is not always true

a) “Someone lives in NY in the United States”

1. Conditional: If someone lives in NY, then the person lives in the United States
2. Converse: If a person lives in the United States, then the person lives in NY
3. Inverse: If the person does not live in NY, then they do not live in the United States
4. Contrapositive: If the person does not live in the United States, then they do not live in NY

Venn Diagram for Conditional Statements

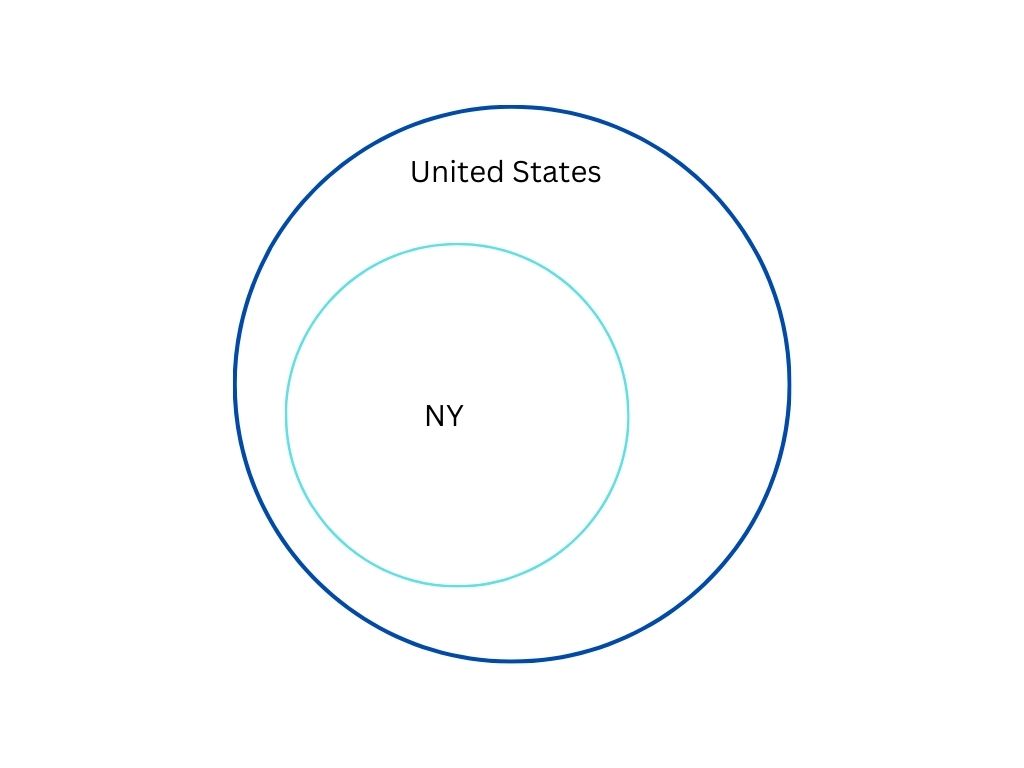Sets

A collection of objects called “elements”

There are two common methods of specifying a set;

• describing the elements of the set with ==words== (“positive integers less than 5”)
• listing the elements of the set between ==set braces==, {}

When Listing Elements

• No repetition: the elements of a set are listed without repetition
  • {1, 2, 2, 3} - incorrect
  • {1, 2, 3} - correct
• Ellipsis: if the set of elements is large, begin the list and then use three dots
  • “Positive integers less than 100” are listed as {1, 2, 3, 4 … }
• Empty set (Null set): if a set has no elements, the set is called the empty set and is denoted by {} or a circle with a diagonal line through it

Naming Sets and Set Elements

• Denotation
  • Naming sets - uppercase letters (A, B, S)
  • Denoting elements of sets - lowercase letters (a, b, s)
  • E.x., A = {a, b, c…}
• Symbol
  • E: an element of a set
  • b is an element of set A, so b E A
  • \