INTRODUCTION TO PHYSICS (9)

• Analysing motion requires physics. The complicated motions are first simplified using physics and then used also using physics.

• The more complicated problems can be simplified by just identifying one simple point, the center of mass of the system of objects.

• For example, if a baseball bat is tossed into air, different parts move at different positions and and in different shapes. However, one point, its center of mass moves in a simple parabolic path.

• Therefore, the centre of mass (com) is used to predict the motion of the whole body.

CENTER OF MASS

• Center of mass of an object is the point that moves as though:

  1. all of the body’s mass was concentrated there

  2. all external forces were applied there.

• First we will locate the center of mass of objects, first of a particle and then of a system of many particles. Later, we will also see how the center of mass changes when external forces are applied on the body.

SYSTEMS OF PARTICLES

• Imagine two masses, m1 and m2 separated by a distance d. The origin of the x-axis is randomly chosen to coincide with the mass m1, and m2 is a distance d away from it.

• The com of this two-particle system is given by

• Suppose, if there is no other particle, then m2 can be taken as 0. This means that the com will be situated at the position of m1.

• If m1=m2, then the com would be at exactly the halfway point between the two particles.

• It is to be remembered that the com lies between 0 and d (between the two masses) if none of the mass is equal to 0.

• Using the coordinates is not necessary. Infact the position of x-axis does not affect the com. If the x-axis is shifted leftwards, the equation can be generalised as:

  

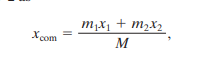
where x1 is the distance between the x-axis and m1, x2 is the distance between m1 and m2, and M is the sum of m1 and m2 (M= m1+m2).

• This equation can be extended to n particles.

  

• If the situation is in three dimensions, the equation above can be further extended to three coordinates:

SOLID BODIES

• Solid objects contain so many atoms that it can be best treated as a continuous distribution of matter. The particles then become differential mass elements dm, and the summations become integrals. The coordinates of the center of mass are then defined as:

• Since all objects can become extremely complex, only objects with uniform density are considered here.

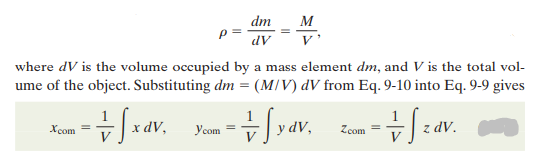
USING SYMMETRY

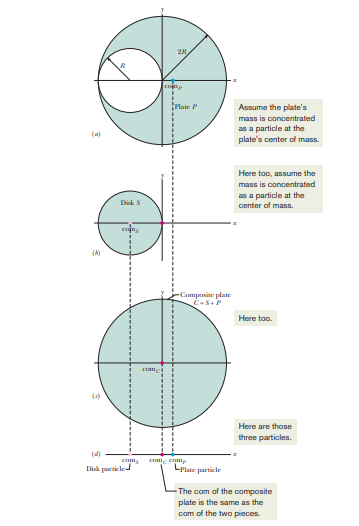
• If an object has a line/point/plane of symmetry, the com lies at that point/line/plane exactly.

• For example, the com of a sphere is exactly at its point of symmetry.

• It is to be remembered that it is not necessary for the object to be at its com, for example, the com of a typical doughnut lies at its center where this is no dough.

  

NEWTON’S SECOND LAW FOR A SYSTEM OF PARTICLES

• Imagine that you hit one billiard ball that is at rest with another. You have an intuitive sense that they will move forward.

• What actually continues to move forward is the center of mass of the two balls (situated exactly halfway between the two balls since they have equal masses).

• We will now observe how the center of mass (which acts like a particle equal to the mass of the whole system) proves the equation F=ma where F is the resultant force of all external forces only, m is the total mass of the system (we assume that mass remains unchanged throughout as it is a closed system), and a is the acceleration of the center of mass.

• This equation is equivalent in all coordinates axes, i.e.

  

• In the case of two billiard balls, during the collision, no external forces act on the balls. Therefore, F=0 which results in a=0 as well. This tells us that the com has no acceleration.

• Since acceleration is the rate of change of velocity, velocity is also equal to zero. This shows that the com moves forward at the same speed and in the same direction after the collision as it was moving previously (after the first ball was hit), and that collision of the two balls has no effect on the motion of the com.

• The equation F=ma also applies to solid bodies, such as a baseball bat. In this case, m is the mass of the bat, and F is the gravitational force on the bat and a (of the com) is equal to the negative of the gravitational force (a=-g).

• Simply, the com of solid bodies move as if they were a single particle of mass m with a force g acting on them.

• It is an interesting fact that the motion of com is not affected by an explosion, but continues in the same path as it would have had there been no explosion. For example in a firework, the explosion is due to internal forces only so there are no external forces that creates no acceleration on the com, causing it to move according to the only external force that has been acting on it, i.e. the gravitational force.

  

LINEAR MOMENTUM

• Linear momentum of a single particle is a vector quantity p defined as the product of m and v where m is the mass of the particle, and v is its velocity.

• Since m is always a positive scalar, p and v have the same direction. This equation also gives the SI unit of momentum as kg.ms^-1.

• Newton also expressed his second law in terms of momentum as: the time rate of change of the momentum of a particle is equal to the net force acting on the particle and is in the direction of that force.

• In equation form, this is:

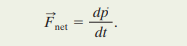
• It is to be remembered that if there is no external force, p cannot change.

LINEAR MOMENTUM FOR A SYSTEM OF PARTICLES

• If we extend this linear momentum to a system of particles each with its own mass and velocity, and who may have external and/or internal forces acting on them, the total momentum is the sum of momenta of all particles.

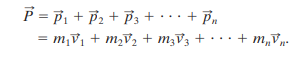
• If we compare this to 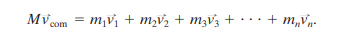which is for a single particle, we see that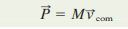

• The linear momentum of a system of particles is thus, equal to the product of the total mass M of the system and the velocity of the center of mass.

• If we take the time derivative, we reach the following equation relating force and momentum

COLLISION AND IMPULSE

• The momentum p of a particle cannot change unless an external force acts on it.

• Sometimes, the external forces are brief but have a large magnitude such as a bat hitting a ball that is at high speed. These collisions suddenly change the momentum of the body.

• Now, we will consider a simple collision of a particle-like body called the projectile and some other body called the target.

SINGLE COLLISION

• Let the projectile be a ball and the target be a bat.

• The bat experiences a force F(t), and changes the momentum p of the ball. This is written in the form of Newton’s second law as dp/dt. This can be rearranged to give:

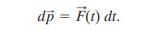
• We can find the momentum of the ball by integrating both sides, setting the limits as tf and and ti which is the time just after and just before the collision respectively.

  

• If we have F and t plotted on the axis, we can find j by finding the area between the curve and the axis.

• The magnitude of the impulse can also be written as the product of average force and change in time of the collision (j= FavgΔt) if we do not exactly know how a force varies with time.

SERIES OF COLLISIONS

• Now we will consider a force which undergoes a series of identical and repeated collisions.

• Imagine a steady stream of identical projectile bodies (e.g. tennis balls) that move with the momentum mv (where m is the mass) along the x-axis (in a straight horizontal line) towards a target fixed in place (e.g. a wall).

• Here we know that each projectile has an initial momentum mv, and undergoes a change in momentum p due to the collision.

• If we take the number of projectiles as n that collide in the time interval p, the total change in linear momentum will be nΔp. The resulting impulse j has the same magnitude but opposite direction so it can be written as j= - nΔp.

• Using the two equations j= FavgΔt and j= - nΔp, we can find the average force acting on the target by the collisions.

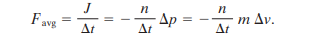
• If projectiles stop within an impact, then we can substitute for Δv in the equation above to find the velocity change.

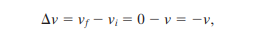
• If projectiles bounce back without the change in speed, vf=-v, and that can be substituted to give:

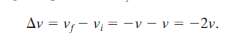
CONSERVATION OF LINEAR MOMENTUM

• If the net external force and the net impulse j on a system of particles is 0, and that the system is isolated, we put F=0 in F=dp/dt, then dp/dt=0. This means that P=0.

• If no net external force acts on a system of particles, the total linear momentum P of the system cannot change.

• This result is called the law of conservation of momentum and is usually written as Pi=Pf, for an isolated closed system.

• If the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum of the system along that axis cannot change.

MOMENTUM AND KINETIC ENERGY IN COLLISIONS

• Until now, we have been focused on the impact on one body only. Now we will see the system as a whole. It is to be remembered that the system here is considered to be closed and isolated.

• The rule previously explained, i.e. the total linear momentum of the system cannot change because there is no net external force to change it, enables us to determine the results of the collision even if we don’t know the details about the collision.

• If we think about the effect of collision on the kinetic energy of the system, there are quite simple, only two situations: either the total energy of the system is the same, i.e. the energy is conserved, or the energy is not the same, i.e. it has been lost in different forms such as sound and thermal energy.

• The collision where the energy is conserved is called an elastic collision.

• The collision where energy is lost and not conserved is called an inelastic collision.

• If bodies stick together after colliding, the collision is said to be a completely inelastic collision.

• Sometimes, it may be approximated for a collision to be elastic, although in real life, most collisions are elastic since energy is always lost.

INELASTIC COLLISIONS IN ONE DIMENSION

• The law of conservation of momentum states as we already know:

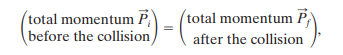which can be symbolised as

but since the motion is one-dimensional, we can drop the vector arrows and use signs for direction,

here, we can find the other final velocity if other terms are known.

ONE DIMENSIONAL COMPLETELY INELASTIC COLLISION

• If we imagine two bodies (calling the moving body projectile and the body at rest target) that undergo a completely inelastic collision, we can say that they stick together and then move together with a velocity V.

• Then we can rewrite the equation

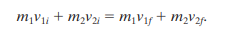as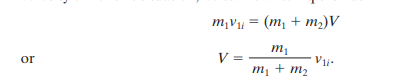

velocity V can be found. It is always less than the initial velocity.

VELOCITY AND CENTER OF MASS

• The com is not changed by the collision in a closed isolated system since there are no external forces on it.

• To observe v com, we can consider a situation as shown below

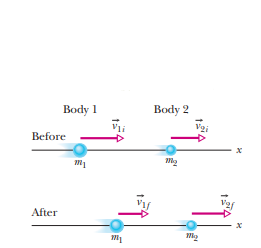here the total linear momentum P can be related to v com by

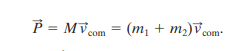since momentum is conserved, it can be represented by either side of the equation. If we substitute the left side

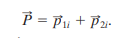we can solve the equation below for v com

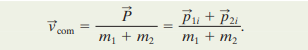It is observed that V has the same constant value before and after the collision.

ELASTIC COLLISIONS IN ONE DIMENSION

• We know that the total kinetic energy remains unchanged in elastic collisions.

• Imagine two pool balls, one of which is stationary, and the other is hit on. The moving ball has the mass m1 and travels with the velocity v1.

• If the system is closed and isolated, linear momentum is conserved and can be written as

we can solve these equations simultaneously to obtain any unknowns we would have to.

SPECIAL SITUATIONS

• Same masses: If m1=m2, then v1f = 0 and v2f = v1i. This means that the moving body stops moving, and the body initially at rest starts moving with the velocity of body 1 (initially moving).

• Massive target: If m2 is much greater than m1 (e.g. m2 is a cannonball and m1 is a snooker ball), then the equations above can be written as

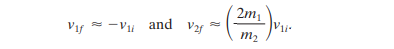this means that m2 would start moving forward at a very low speed, and m1 would bounce back at the same speed.

• Massive projectile: In this case, m1 is much larger than m2. The larger body simply keeps moving at a slow speed, but the lighter body charges at twice the speed.

• For a case where both bodies are moving, linear momentum is written as

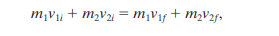and the kinetic energy is written as

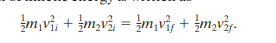these equations can be simultaneously solved for the unknowns.

In two dimensions, impulse determines the direction, If the collision is not head-on, the bodies do not travel along the initial axis. But for a closed isolated system, the momentum is conserved. In elastic collisions, kinetic energy is also conserved.

SYSTEMS WITH VARYING MASS LIKE ROCKETS

• Until now, we have had a constant mass. Sometimes, when mass is not constant such as in a rocket where fuel is ejected, Newton’s second law is applied to the rocket and the ejected fuel as a whole.