Seed Concepts of Geometry

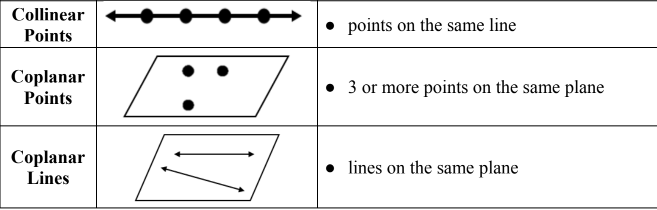
The point, line, and plane are the seed concepts of geometry. Although they are abstractions or mathematical ideas based on our experience, they form the starting point of the description of geometrical structures. They are often called “undefined terms.”

Point

A point is represented with small dots. It has no dimension. We use a capital letter to name a point.

notation:

point A, point B, point C, point D

figure:

Line

A line has no width and it is extended endlessly in both directions. It has one dimension: length.

We use a lower-case letter or any two points on the line to name a line.

notation:

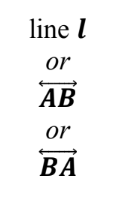
figure:

Plane:

A plane is a flat surface that extends infinitely far in all directions. It has no thickness. We use a capital script letter or three non-collinear points on the plane to name a plane.

notation:

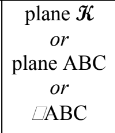
figure:

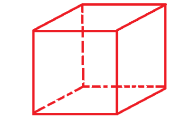
Space

A set of all points. It extends infinitely in all directions and has three dimensions.

figure:

Basic Postulates

Postulates are statements of facts or self-evident truths. It is accepted as true without proof. In Filipino, “malinaw na katotohanan”.

Postulate 1: Points Postulate -

● A line contains at least two points.

● A plane consists of at least three non-collinear points.

● A space contains at least four non-coplanar points.

Postulate 2: Line Postulate - Two points determine a line.

Postulate 3: Plane Postulate - Three non-collinear points determine a plane.

Postulate 4: Flat Plane Postulate - If two points of a line lie on the plane, then the entire line lies on the plane.

Postulate 5: Plane Intersection Postulate - If two planes intersect, then their intersection is a line.

Postulate 6: Ruler Postulate -

● For every pair of points, there is only a positive real number called the distance between the two points.

● The length or linear measure of a segment is the distance

between its endpoints. This distance is denoted AB for a segment.

Postulate 7: Segment Construction Postulate - On any ray, there is exactly one point at a given distance from the endpoint of the ray.

Postulate 8: Segment Addition Postulate - If point P is between A and B, then the linear measures AP̅̅̅̅ + PB̅̅̅̅ = AB̅̅̅̅.

Theorems

Unlike postulates, theorems are statements that must be proven true by citing undefined terms, definitions, postulates, and other proven theorems.

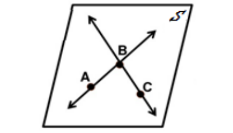
Theorem 1: Line Intersection Theorem - If two lines intersect, then

their intersection is exactly one point.

Thereom 2: Line-Point Theorem - Given a line and a point

not on the line, there is exactly one plane that contains them.

Thereom 3: Line-Point Theorem - Given two intersecting

lines, there is exactly one plane that contains the two lines.

Theorem 4: Line-Plane Intersection Theorem - Given a plane and a line

not on the plane, their intersection is one and only one point.

Angle Pairs I

Supplementary Angles - If the sum of the measures of two angles is 180°, then they are called

supplementary angles.

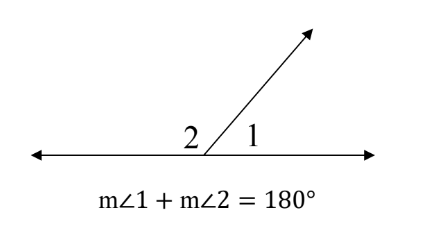
Complementary Angles - If the sum of the measures of two angles is 90°, then they are called complementary angles.

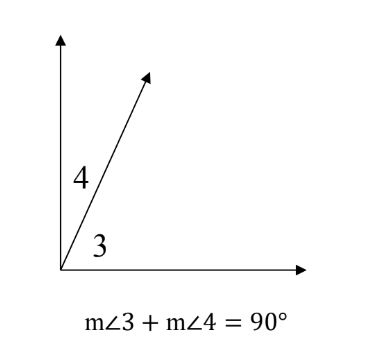
Two angles don’t need to be adjacent to be called supplementary or complementary.

Angle Pairs II

Adjacent Pairs - two angles with a common vertex, a common side, and no common interior points.

In the figure, ∠AEB and ∠BEC share a common vertex at point E and a common side at ray EB . These pair of angles are adjacent angles. ∠BED and ∠CED are NOT adjacent angles since point C is in the interior of ∠BED.

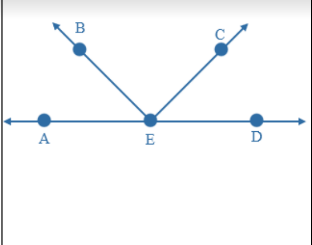
Linear Pair of Angles - a pair of adjacent angles whose non-common sides are collinear. The sum of the measures of the angle is 180°.

Example: ∠DBA and ∠DBC are a linear pair because ray BA and ray BC are collinear.

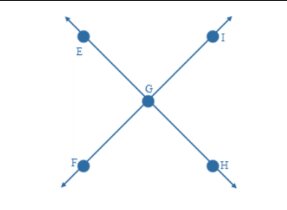
Vertical Angles - pair of angles opposite each other formed by two intersecting lines in an “X”-shape. Vertical angles are equal in measure and so are congruent.

Example:∠EGI and ∠FGH are vertical angles which means that they are congruent.

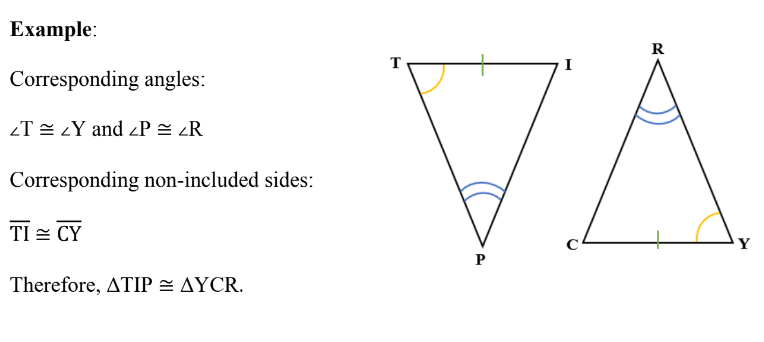
Types of Triangles

● A right triangle is a triangle with a right angle. It is composed of two legs and a

hypotenuse (the side opposite the right angle). (Figure 1)

● An acute triangle is a triangle with three acute angles. (Figure 2)

● An obtuse triangle is a triangle with an obtuse angle. (Figure 3)

● An equiangular triangle is a triangle with three equal angles. (Figure 4)

● An equilateral triangle is a triangle with three equal sides. (Figure 5)

● An isosceles triangle is a triangle with two equal sides. (Figure 6)

● A scalene triangle is a triangle with no equal sides.

Acute angle - less than 90 degress

obtuse angle - more than 90 degrees less than 180 degrees

Corresponding Angle

Corresponding angles of two triangles are the angles whose vertices are

matched.

If we match or pair vertex B with vertex E, vertex A with vertex D, and vertex

C with vertex F, we get the correspondences:

∠B ↔ ∠E AB ↔ DE

∠A ↔ ∠D BC ↔ EF

∠C ↔ ∠F AC ↔ DF

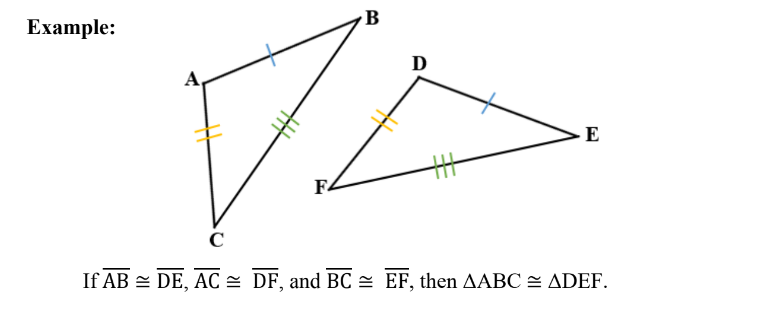
Congruent Triangle

Two triangles are congruent if and only if there is a matching of their vertices such that corresponding parts are congruent.

In most references, this is known as the CPCTC (Corresponding Parts of

Congruent Triangles are Congruent) Theorem.

Note: The symbol ↔ means “corresponds to”.

SSS (Side-Side-Side) Congruence Postulate

If three sides of one triangle are congruent to the corresponding sides of

another triangle, then the triangles are congruent.

SAS (Side-Angle-Side) Congruence Postulate

If two sides and the included angle of one triangle are congruent to the

corresponding parts of another triangle, then the triangles are congruent.

Note: The “included angle” is the angle whose vertex is the common endpoint of the two sides.

ASA Congruence (Angle-Side-Angle) Postulate

If two angles and the included side of one triangle are congruent to the

corresponding parts of another triangle, then the triangles are congruent.

Note: The “included side” is the side whose endpoints are the vertices of the two angles.

AAS (Angle-Angle-Side) Congruence Postulate

If two angles and a non-included side in one triangle are congruent to the

corresponding parts of another triangle, then the two triangles are congruent.