The Metric System (Unit 1)

* the ones that need to be memorized

Scientific Notation (Unit 1)

• a way of writing numbers that accommodates values too large or small to be conveniently written in standard decimal notation

  • basic form of a number in scientific notation is:

    a x 10^b (where 10 > a ≥ 1 and b is an integer)

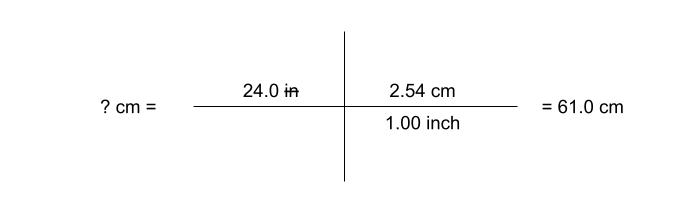
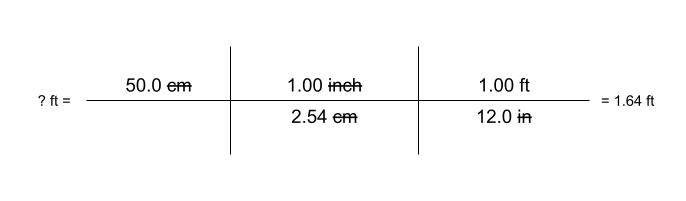
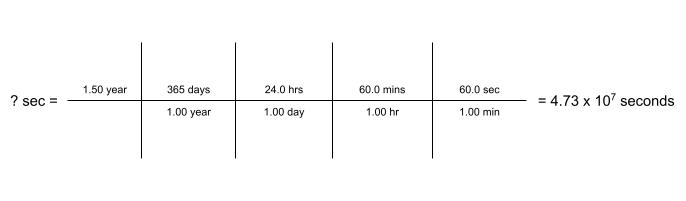
Dimensional Analysis (Unit 1)

• Dimensional Analysis - a problem-solving method that uses the fact that any number or expression can be multiplied by one without changing its value

Examples:

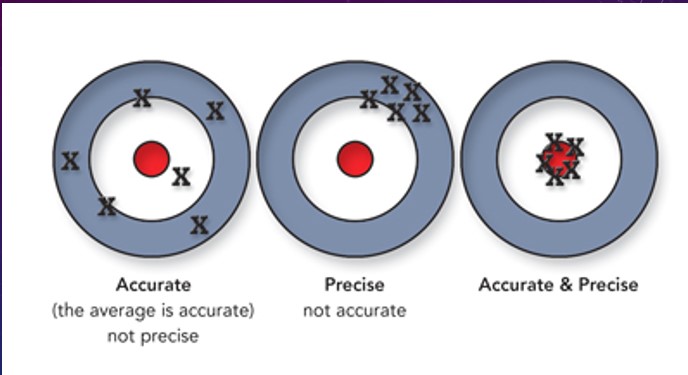
Precision and Accuracy (Unit 1)

• Accuracy - the agreement between experimental data and a known value

• Precision - how well experimental values agree with each other

data can be very precise such that each data point is close to the others, yet contain a high degree of experimental error

Significant Figures (Unit 1)

digits that are taken in a measurement significant digits; when doing math with significant digits, we have rules to keep us from taking the small errors in each number into larger errors in our final answers

we have some rules:

1. any number that is not a zero is significant

2. for zeros:

   A. leading zeros are zeroes that precede all the nonzero digits. They do not count as significant figures. In the number 0.0025, the three zeros simply indicated the position of the decimal point. this number has only two significant digits

   B. captive zeros are zeros that are between two nonzero digits. these always count as significant figures. the number 1.008 has 4 significant figures

   C. trailing zeros are zeros at the right end of the number. they are significant only if the number contains a decimal point. the number 100 has only 1 significant digit, whereas the number 100.0 has 4. the number 100. has 3 significant figures

for a number in scientific notation, all numbers are significant:

3.21 × 10¹² m has three significant figures

Gases (Unit 2)

pressure (P), temperature (T), volume (V), number of particles (n)

as V↑, P↓; and as V↓, P↑ → inversely proportional, often known as Boyle’s Law

as n↑, P↑; and as n↓, P↓ → pressure and number of particles are directly proportional

as T↑, P↑; and as T↓, P↓ → directly proportional, only exists when the temperature is in terms of absolute temperature (Kelvin) K = °C + 273.15 ; known as Gay-Lussac’s Law

as T↑, V↑; and as T↓, V↓ → directly proportional, temperature must be expressed in Kelvin; called Charles’ Law

Kinetic Molecular Theory (KMT):

• particles of gas are in constant random motion, moving in straight lines until they collide with another particle or a wall of the container in which they are enclosed

• particles of gas do not eventually slow down. in physics terms we say they only experience “elastic” collisions

• particles of gas do not stick to other particles

• the speed of gas particles is related to their temperature

• the pressure of gas is related to the frequency and speed of the collisions of the gas particles with the sides of the container in which they are enclosed

Laws - predictive, they help us to predict something if we have some other information; often mathematical expressions

Theories - explanatory, they help us explain the regularities that we observe; well-substantiated explanation of some aspect of the natural world that is acquired through careful research and repeatedly confirmed through observation and experimentation

Standard Temperature and Pressure (STP): 273 K (0°C) and 1.00 atm

Solving Gas Problems:

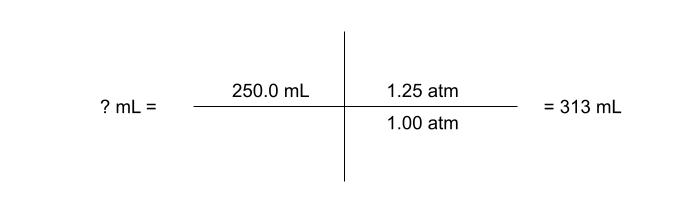
A gas occupies 250.0 mL at 1.25 atm. What is the volume of the gas if the pressure decreases to 1.00 atm?

now we are ready to solve the problem using ratios. begin with the give of what we are trying to solve for (in this case volume), then write the ratio of the pressure next to it, so that it will have the effect we desire. since we know that the volume should get bigger, the larger of pressure goes on top of the fraction

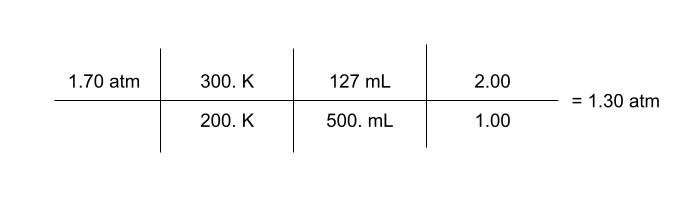
A piston with an initial volume of 127 mL at 1.70 atm and 200. K is changed to a volume of 500. mL and a temperature of 300. K. When it changes, some gas leaks in and the number of particles doubles. What is the final pressure?

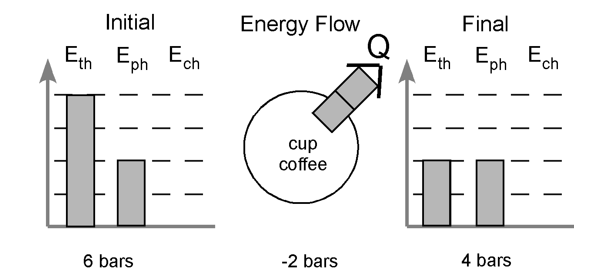
Energy Bar Charts (Unit 3)

due to interactions between particles, the energy stored due to the arrangement of particles is ranked:

solids < liquids < gases

we choose to represent these phases by using:

• solids = 1 bar

• liquids = 2 bars

• gases = 4 bars

example:

Quantifying Thermal Energy (Unit 3)

The First Law of Thermodynamics: the law of conservation of energy is an empirical law of physics. it states that the total amount of energy in an isolated system remains constant over time (is said to be conserved over time). a consequence of this law is that energy can neither be created nor destroyed: it can only be transformed from one state to another

measure the flow of energy and the change in temperature in Joules (J)

quantity of heat required to raise the temperature of a gram of a substance by one degree Celsius is called Specific Heat of the substance (also known as the heat capacity). measured in units of Joules

to calculate the heat it takes to change the temperature of a substance, you can use the following equation:

Q =mc∆T

• Q = the heat absorbed (if positive) or released (if negative)

• m = the mass of the substance

• c = specific heat of the substance (determined experimentally or looked up in a table)

• ∆T = the change in temperature (final temperature - initial temperature)

examples:

How much energy is required to raise the temperature of 100.0 grams of water from 25.0°C to 35.0°C? The specific heat of water is 4.184 J/g°C.

m = 100.0 g

c = 4.184 J/g°C

∆T = T_final - T_initial = 35.0°C - 25.0°C = 10.0°C

Q = mc∆T

Q = (100.0 g) (4.184 J/g°C) (10.0°C)

Q = 4180 J = 4.18 kJ, so 4.18 kJ of heat are absorbed

What is the final temperature of a 10.0g piece of ice initially at -5.00°C if 2.55 kJ of heat are removed from it? The specific heat of ice is 2.093 J/g°C.

m = 10.0 g

c =2.093 J/g°C

Q = -2.55 kJ = -2550 J

T_initial = -5.00°C

Q = mc∆T

-2550 J = (10.0 g) (2.093 J/g°C) ∆T

∆T = -122°C

∆T = T_final - T_initial

T_final = ∆T + T_initial = 122°C + (-5.00°C) = -127°C

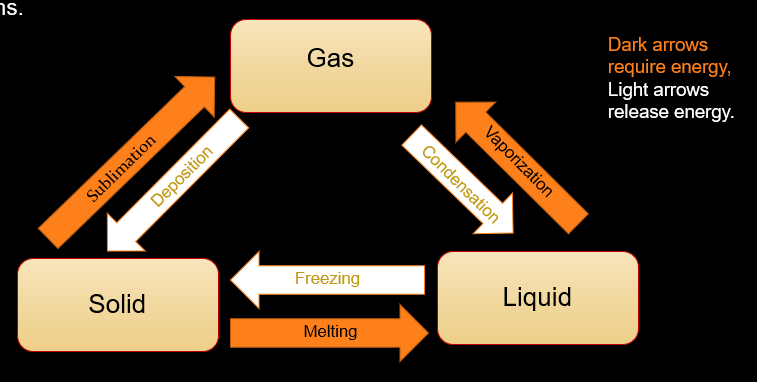phase changes occur when a substance goes from being in one state to another (not chemical reactions)

to calculate the energy involved in a change of state, we use a formula similar oto teh earlier formula. since there is no temperature change, there is no ∆T in the formula. also, instead of specific heat, we use the Heat of Vaporization (for changes between liquid and gas) or Heat of Fusion (for changes between liquid and solid).

Q = mH_v or Q = mH_f

For water,

H_vaporization = 2260 J/g

H_fusion = 334 J/g

examples:

m = 10.0 g

H_f = 334 J/g

Q - mH_f

Q = (10.0 g) (334 J/g)

Q = 3340 J are required to melt 10.0 g of ice

How much heat is absorbed when 10.0 g of ice at 0.00°C is melted and then the water is heated to 50.0°C?

m = 10.0 g

T_i = 0.00°C

T_f = 50.0°C

Q = mH_f + mc∆T

Q = (10.0 g) (334 J/g) + (10.0 g) (4.184 J/g°C) (50.0°C - 0.00°C)

Q = 3340 J + 2090 J

Q = 5430 J

How much energy, in kJ, is absorbed when 5.00 g of water at 20.0°C is boiled and becomes stem at 100.°C? The specific heat of water is 4.184 J/g°C and the Heat of Vaporization of water is 2260 J/g.

Q = mc∆T + mH_v

Q = (5.00 g) (4.184 J/g°C) (100.°C - 20.0°C) + (5.00 g) (2260 J/g)

Q = 1673.6 J + 11,300 J

Q = 12973.6 J = 13,000 J = 13.0 kJ

Describing Substances (Unit 4)

matter occurs in three states:

• gas → the particles are freely moving around very rapidly with a lot of space between. gases fill the entire volume of the container they are in. because the particles are so far apart, gases can be compressed easily

• liquid → the particles are not rigidly held together but are closer together than in a gas. liquids have a constant volume but will take the shape of the container they are in. they are difficult to compress

• solids → the particles are held in specific places giving the solid and definite form and volume. they are tightly packed and can’t be compressed

less common states of matter:

• plasma → formed when a gas is superheated and the electrons are stripped away

• bose-einstein condensates → a superfluid that forms when some elements are cooled to near absolute zero

matter can also be identified by its properties:

• physical properties → things that are observed without changing the sample’s composition. things like color, odor, hardness, or melting point are physical properties

  • extensive properties → depend on the amount of a substance present. length, volume, and mass are all extensive properties. the more of the substance you have, the higher the value

  • intensive properties → independent of the amount of substance present. boiling point, specific heat, color, and density are examples

• chemical properties → characteristics that can only be seen when a substance reacts with another substance. some examples are reactivity, toxicity, and flammability

chemical and physical changes:

• chemical changes → require a substance to undergo a chemical reaction. we can usually tell when this happens because of what we detect. giving off heat or light is a sign of chemical change, like when we burn a log in a fire. there are other signs of chemical changes: giving off bubbles, changing color, giving off an odor, or forming a precipitate are all sign a chemical change is occurring

• physical changes → the chemical composition of the substance remains the same; two types of changes:

  • change in state - when water turns to ice, the particles are still water particles made of one oxygen atom and two hydrogen atoms

  • changing something about how the particles are arranged - cutting a piece of paper into two pieces is a physical change. it is still paper

pure substances and mixtures:

• pure substances → fall into two categories:

  • elements - substances that can’t be broken down in simpler particles without losing their chemical identity. so hydrogen gas, a bar of gold, or the mercury in a thermometer are all elements

  • compounds - combinations of elements that always occur in exactly the same proportions. in carbon dioxide, CO₂, there are always one carbon atom and two oxygen atoms

• mixtures → not pure substances. they are combinations of elements or compounds but have no fixed composition. coffee can be strong or weak, can contain milk or sugar or both. the air in the room that you are breathing is a mixture of mostly nitrogen and oxygen, but it can contain a lot of other things… carbon dioxide, water vapor, helium, dust particles…; can be divided into two kinds:

  • homogeneous mixtures - have a constant composition throughout. and example would be salt dissolved in water. the salt dissolved uniformly in small particles and is evenly distributed everywhere in the water

    • solutions are homogeneous mixtures

  • heterogeneous mixtures - do not bled smoothly together so individual substances remain distinct. oil mixed with water is a heterogeneous mixture

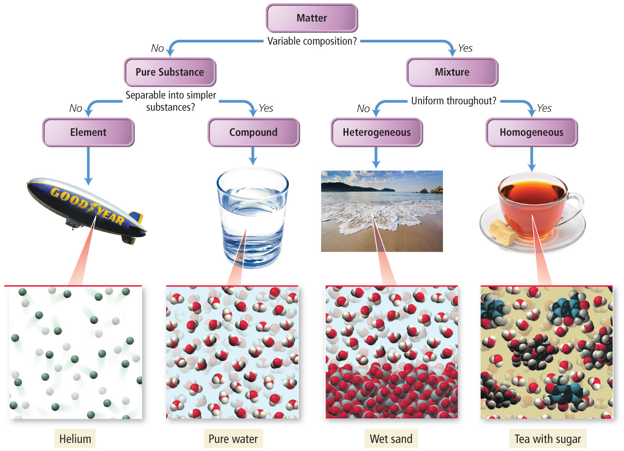compounds are chemical combinations of two ore more elements and their properties differ from the properties of their component elements

methods of mixture separation:

• filtration → passing a liquid through a filter to remove larger particles while letting smaller ones pass through

• distillation → used to separate two mixtures with very different boiling points. the temperature is raised and the lower boiling liquid turns to a gas leaving the other liquid behind

• crystallization → used to get a solid out of a liquid. it requires a highly saturated solution of the solid and then addition of a see crystal

• sublimation → used to purify compounds or separate in sublimation apparatus and heated under vacuum. under this reduced pressure the solid turns into a gas and condenses as a purified compound on a cooled surface leaving a residue of impurities behind

• chromatography → separates two or more dissolved substances in a liquid. it uses the fact that large molecules dissolved in liquid will move slower than small molecules when they pass through a media, such as paper

• evaporation → used to remove a liquid from a solid

Dalton and the Law of Definite Proportions (Unit 4)

John Dalton (1766-1844), an english chemist, physicist, and meteorologist, in 1802 presented his ideas about atoms. these were not his alone. but he was the first to put together a clear presentation of all that was currently thought about the atom at this time.

Dalton’s Atomic Theory

1. All matter is made of elements. elements are made of tiny particles called atoms

2. Atoms cannot be created, divided into smaller particles, nor destroyed in the chemical process; a chemical reaction simply changes the way atoms are grouped together

3. The atoms of a given element are different from those of any other element; the atoms of different elements can be distinguished from one another by their respective relative atomic weights

4. All atoms of a given element are identical

5. Atoms of one element can combine with atoms of other elements to form chemical compounds; a given compound always has the same relative numbers of types of atoms

law of definite proportions - a compound is always composed of the same elements in the same proportions (discovered by Joseph Proust)

you can calculate the percentage of a compound that is made of an element using the following formula:

percent by mass can be used to determine if two sample compounds are possibly the same substance. if they are the same, they must have the same percent composition. this is not sufficient to prove they are the same, but if they have different percent compositions, it proves they are not the same

New Model of the Atom (Unit 5)

Sir William Crookes - (during 1870s) developed the first cathode ray tube to have a high vacuum inside; showed that luminescence rays appearing within the tube carried energy and moved from the cathode ray to the anode; the ray behaved as though it were negatively charged

J.J. Thomson - (in 1897) indicated that cathode rays really were unique particles, rather than waves, atoms or molecules as was believed earlier; usually credited for discovering the electron; “corpuscles” had perhaps one thousandth of the mass of the least massive ion known: hydrogen

George F. Fitzgerald - proposed the name electron, and has since gained universal acceptance

Robert Millikan - (in 1909) performed the oil drop experiment to measure the charge of the electron

• oil drop experiment

  • balancing the downward gravitational force with the upward buoyant and electric forced on tiny charged droplets of oil suspended between two metal electrodes

  • confirmed that the charges were all multiples of some fundamental value, and calculated it to be 1.5924 × 10^-19 C, within one percent of the currently accepted value of 1.602176487 × 10^-19 C. this was the charge of a single electron

plum pudding model - the electrons were thought to be scattered throughout the atom much like the plums would be in plum pudding or chocolate chip cookies

nucleus - very dense region consisting of nucleons (protons and neutrons) at the center of an atom; almost all of the mass in an atom is made up from the protons and neutrons in the nucleus, with a very small contribution from the orbiting electrons; discovered in 1911, as a result of Ernest Rutherford’s interpretation of the famous 1909 Gold Foil Experiment.

• gold foil experiment

  • beam of a positively charged alpha particles was directed onto a sheet of very thin gold foil; gold foil surrounded by a circular detector

  • alpha particles should all have been deflected by, at most, a few degrees; measuring the patter of scattered particles was expected to provide information about the distribution of charge within the atom

  • he observed that a very small percentage of particles were deflected through angles larger than 90 degrees.

Rutherford expected to see that all the alpha particles would pass through the gold foil un-deflected, with a few occasionally deflected by an electron. he found was that some particles deflected much more than anticipated and some even came back toward the source. this meant that the positive charge inside the atom was small and heavy and concentrated in the center of the atom

Rutherford planetary model - (by 1920) refined this model and said the nucleus was contained positively charged particles called protons.

James Chadwick - (in 1932) discovered that the nucleus contained a second particle that had almost the same mass as a proton but no charge; called it neutron.

Even Newer Model of the Atom (Unit 5)

top of the wave is called the crest and the bottom is called the trough.

the length of the wave is called the wavelength and is represented by λ, it can be measured from crest to crest or trough to trough or any other consistent way.

the height of the wave is called the amplitude. this is a measure of the energy carried by the wave

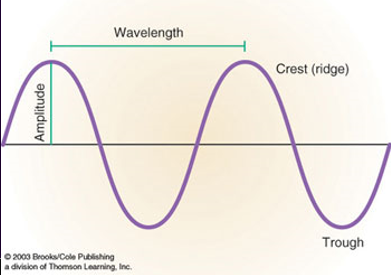
the frequency of a wave is how many waves pass a given point in a second, and is represented by 𝛎; as frequency increases, wavelength decreases, assuming the waves are moving at the same speed.

we are only concerned with light waves, so we only have to know one speed: the speed of light, c.

c = 3.00 × 10⁸ m/s

the relationship between frequency, wavelength, and speed combine into a very simple formula.

c = λ𝛎

where c is the speed of light in m/s, λ is the wavelength in meters, and 𝛎 is the frequency in cycles per second, or more commonly, just sec^-1.

we see light in only a small part of a larger kind of energy called electromagnetic radiation. this radiation comes in all wavelengths. we call this the electromagnetic spectrum.

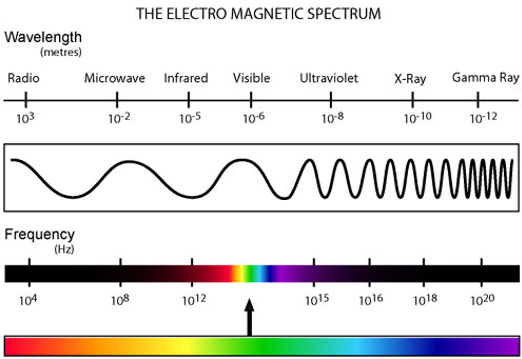
In the 1600s, Christian Huygens and Issac Newton proposed competing theories for light’s behavior. Huygens proposed a wave theory of light while Newton’s was a “corpuscular” (particle) theory of light. Huygens’ theory had some issues in matching observation. Newton’s prestige helped lend support to his theory, so for over century his theory was dominant.

Max Planck reached the conclusion that energy moved in discrete packets called quanta. so a quantum was this minimum amount of energy that could be moved. before this idea, they thought energy could be transferred in units of any size. it just turns out the quanta are so small, no never noticed them before.

energy of radiation can be determined by the following equation:

E_quantum= h𝛎

energy of the photon can be calculated using the following formula:

E_photon= h𝛎

where E is energy in Joules, h is Planck’s constant (6.626 × 10^-34 J·s), and 𝛎 is the frequency of the radiated light, in Hertz (or sec^-1).

photoelectric effect - a light source (or, more generally, electromagnetic radiation) strikes a metallic surface, the surface can emit electrons; electrons emitted in this fashion are called photoelectrons (although they are still just electrons). the problem was, that it didn’t work like the wave model of light said it should

wave-particle duality - the concept that all matter exhibits both wave and particle properties