def. reverts the x and y values of a function, values must be one to one to have an inverse function

e.g.

has an inverse function

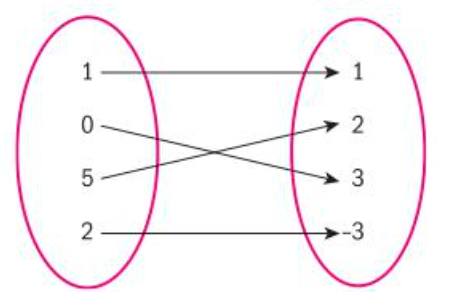
does not have an inverse function

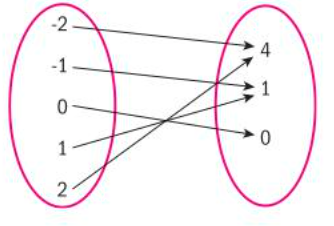
• swaps the x and y values

• domain and range are swapped

  e.g. f = 3<x<8, f-1 = 3<y<8

• regular function and inverse function will intersect at x=y

• x and y intercepts are swapped

  e.g. f = (0,3) (5,0), f-1 = (0,5) (3,0)

GRAPHING INVERSE FUNCTIONS

E.g.1

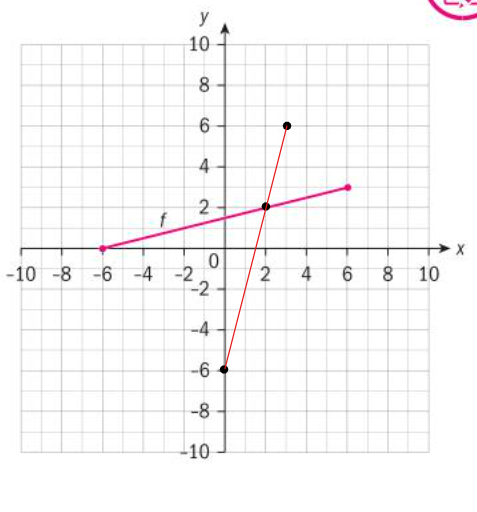regular points = (-6,0), (2,2) and (6,3)

inverse points = (0,-6), (2,2) and (3,6)

E.g.2

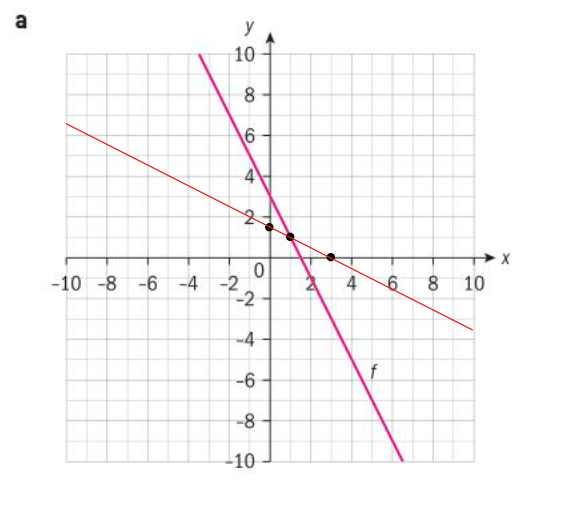
regular points = (0,3), (1,1) and (1.5,0)

inverse points = (3,0), (1,1) and (0,1.5)

E.g.3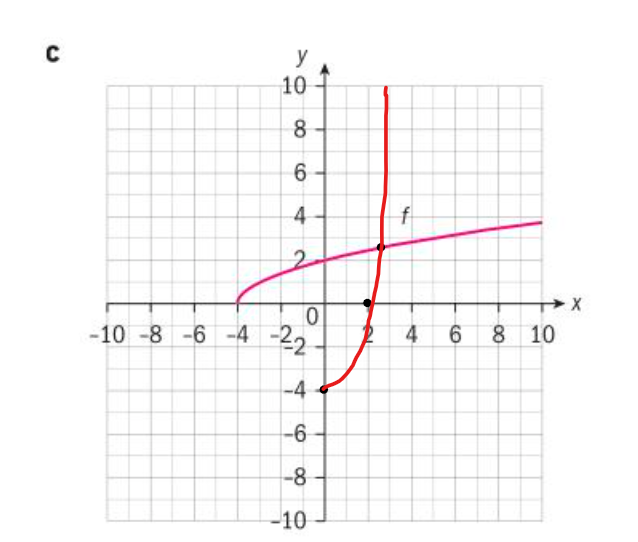
regular points = (-4,0), (0,2) and (2.5,2.5)

inverse points = (0,-4), (2,0) and (2.5,2.5)

IMPORTANT POINTS

• y-intercept

• x-intercept

• point where x = y - e.g. (2,2) or (1,1) or (-4,-4)

Oxford IB Textbook : Exercises 5G and 5H