Describing Motion

If we wish to understand how and why objects move as they do, we have to set up a basic language framework.

• What is the precise meaning of the words we use?

For the time being we shall treat every object as a point particle.

• point particles have no size so they do not rotate.

First thing we need is a Reference Frame in order to say where the object is in space. We pick some point in space and call it The Origin.

The position of an object is described by a set of coordinates.

• We shall use Cartesian coordinates x, y, z but there are others

Position is a vector quantity.

• It is different from distance.

• The size of the position vector is the distance from the origin, the vector points from the origin to where the object is

• We shall regard Time as a separate dimension. Let’s consider an object which changes its position.

Average Speed and Velocity

The average speed of the object is:

• average speed= distance moved/time interval

Average speed is a scalar.

Average velocity is a vector: the size of the vector is the average speed, the average velocity vector points in the direction of motion.

The average velocity v of the object is just:

• average velocity= displacement/time interval

EXAMPLE 1:

The position of a runner as a function of time is plotted as moving along the x axis of a coordinate system. During a 3.00-s time interval, the runner’s position changes from x1 = 50.0 m to x2 = 30.5 m, as shown. What was the runner’s average speed and average velocity?

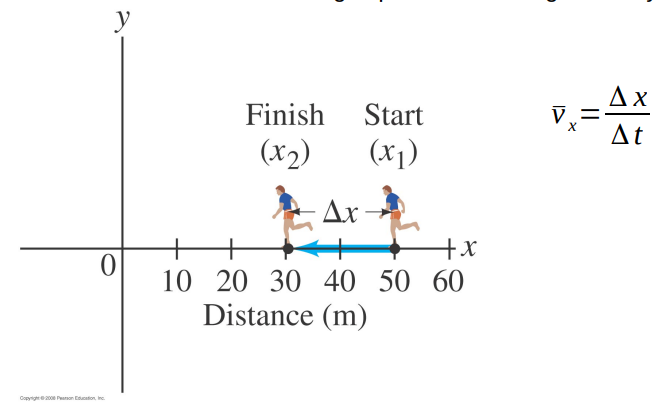
• v_x = Δ x/Δt

• -20 / 3 = -6.66m/s

EXAMPLE 2:

A batter hits a home run during a softball game and rounds the bases in 20 seconds. What is her average velocity starting from when she starts running to when she crosses home plate? FYI, the bases of a softball diamond are 60 feet apart.

• Zero

• Average velocity is the displacement divided by the time elapsed. Her displacement as she crosses home plate is zero – she has the same position vector at the beginning and end of her run.

Instantaneous Velocity

More generally the velocity (and speed) of an object is not constant.

The instantaneous velocity v is the velocity at a given instant in time.

• If you were driving a car, it’s the reading on the speedometer.

• Instantaneous velocity is still a vector.

• The ‘Instantaneous’ part is often dropped.

Relative Motion

The speed/velocity and thus the motion of an object are relative to the origin of the Reference Frame.

In a different Reference Frame the object’s speed/velocity will be different and its motion will also look different.

• Consider two trains approaching one another.

• 

• What are the speeds of the trains according to someone standing by the track?

  • The Reference Frame for this person is stationary for them. What are the speeds of the trains according to the driver of the red train?

  • Who uses a Reference Frame that is stationary for them.

• Consider a boat crossing a river.

• 

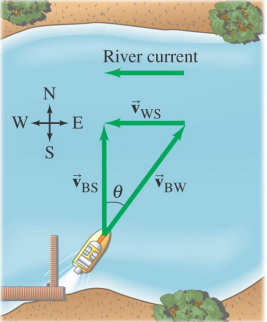
• Someone standing on the shore sees the boat go straight across. The driver of the boat says she had to head slightly upstream against the current.

  • They are both right.

Acceleration

An object’s instantaneous velocity can change in two different ways (sometimes it does both at the same time).

• its size can change (speeds up, slows down)

• its direction can change (the speed can stay the same)

Acceleration is the rate of change of velocity.

The average acceleration is the change in velocity divided by the time it takes to make the change.

• average acceleration= change in velocity/time interval

The instantaneous acceleration is the acceleration at a given instant in time.

• If your car had one, it would be the reading on an accelerometer.

EXAMPLE 1:

An automobile is accelerating when it is

• A. slowing down,

• B. speeding up,

• C. rounding a curve,

• D. all of the above.

• E. none of the above.

C) All of the above

Change in speed (increase or decrease) per time is acceleration, so slowing is acceleration. Change in direction is acceleration (even if speed stays the same), so rounding a curve is acceleration.

QUESTION 1:

Can an object have a velocity which is zero but and acceleration which is not zero at the same time?

• Yes, when you start a car.

QUESTION 2:

There are two objects A and B. If the velocity of A is greater than the velocity of B, vA > vB , does that mean the acceleration of A is greater than that of B?

• No, not necessarily, since velocity and acceleration are different.

Free Fall

From experiment Galileo discovered that:

• In the absence of air resistance, all objects fall with the same acceleration

• We call this acceleration the acceleration due to gravity.

  • Its symbol is g.

Gravimetry is the measurement of the acceleration due to gravity.

The acceleration due to gravity points downwards, towards center of the Earth.

• g varies with height above the Earth but over a large scale.

  • of order 100 km,

• There is a some small variation with location on the surface of the Earth.

  • this variation is due to composition of the local rocks and the shape of the Earth.

  • large nearby masses – such as mountains – can change the direction by very small angles

• g’s value is approximately 9.81 m/s2 .

  • at the poles g is actually slightly larger than this, 9.83 m /s2

  • at the equator it is slightly smaller, 9.78 m /s2

• We will use 10 m/s2 for g.

  • An acceleration of 10 m/s2 means an object’s velocity changes by 10 m/s every second in the direction of the acceleration.

• Consider an object thrown upwards with an initial velocity of 30 m/s. After the object leaves the thrower’s hand, the object has a constant acceleration of g downwards.

  • During the first second the object has an average upwards velocity of 25 m/s so it travels 25 m during this time.

  • During the second second it has an average upwards velocity of 15 m/s so it travels 15 m during this period.

  • During the third second it has an average upwards velocity of 5 m/s so it travels 5 m during this period.

  • After three seconds of flight the object has zero upwards velocity. It has traveled a total distance of 25 m + 15 m + 5 m = 45 m.

• 

• Consider an object which is dropped from a tall tower. If it’s velocity at time zero is zero then:

  • At 1 s its velocity is 10 m/s and down

  • At 2 s its velocity is 20 m/s and down

  • At 3 s its velocity is 30 m/s and down

  • At 4 s its velocity is 40 m/s and down.

  • Let’s say the object takes t seconds to hit the ground. What is it’s average velocity from zero to t seconds?

    • average velocity= 1/2 gt

• How far does an object move in time t if its average velocity is:

  • 10 m/s and down

  • 20 m/s and down

  • 30 m/s and down

  • ½ g/t and down

  • So if it takes t seconds for an object released from a tall tower to hit the ground, the distance d the object falls must be

    • d= 1/2×g×t×t= 1/2 gt^2

EXAMPLE:

What is the distance fallen after 4 s for a freely falling object starting from rest?

• A. 4 m

• B. 16 m

• C. 40 m

• D. 80 m

D) 80 m

(1/2)(10 m/s^2)(4 s)(4 s) = 80

EXAMPLE:

When throwing a ball straight up, which of the following is true about its velocity v and its acceleration a at the highest point in its path?

• (1) v = 0 and a = 0.

• (2) v = 0 but a ≠ 0.

• (3) v ≠ 0 but a = 0.

• (4) v ≠ 0 and a ≠ 0.

2) v = 0 but a ≠ 0.