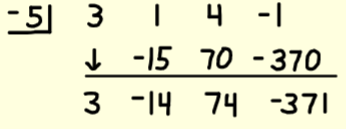Test 1 Study Guide (copy)
Piecewise functions
f(x) = {
Plug in values appropriately and solve (if it doesn’t work put undefined)
Graph using an open circle for less/greater than and a closed circle for less/greater or equal than
Find the domain and range based on the graph (use {3} and U for singular values)
Discontinous = break in the graph, x = [number]
Show work for hole, vertex, and 2 points of parabola
To find the graph of functions with holes, factor parts and try to cross out anything that cancels
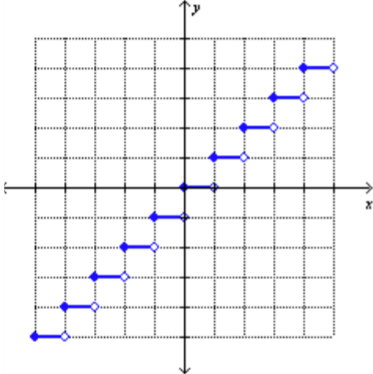
Greatest integer functions
Marked by [[x]]
Apply transformations as usual
To find values, find the greatest integer less than or equal to x and apply transformations
Writing absolute value as piecewise
Set the original greater than or equal to 0
Solve for x, that is your first “for”
Find the opposite (switch all signs) of the original and set it greater than 0
Solve for x again, that is your second “for” and should be opposite
Synthetic division (basic operation)
P(x) is product aka what they give you, (x-c) is the divisor, q(x) is the quotient/your answer and r is the remainder
Put the c in the top left (c = -5 or x+5)
Put all the coefficients of the equation in order with their signs (if a term is skipped put a 0)
Pull down the first number
Multiply each bottom number by the top left and put it under the next term (3 x -5 = -15)
Continue until done
The last number is the remainder, the first few numbers are coefficients of the quotient/answer
Plug it into the forms given
Remainder Theorem
If a polynomial is divided by x-c, the remainder is P(c)
Use synthetic division on the P they give you, as is (if you have P(4) then put 4 in the top left and divide the equation as normal)
The answer is the remainder/the last number
Big degrees = big numbers
Factor Theorem
A polynomial has factor x-c if and only if P(c) = 0
If r = 0, x-c is a factor of P(x)
Answer with yes or no
Use the x = as your left number and divide normally
If the remainder is 0 then it is a factor
Intermediate Value Theorem (IVT)
If P(a) and P(b) have opposite signs, then P(x) has a real zero in the interval [a, b]
Do synthetic division for both numbers
If the sign for the remainder changes (one is pos, one is neg), then the theorem applies (there is a solution in the interval)
Change in sign. By IVT,
If the sign does not change, the theorem cannot apply
Same sign. IVT does not apply.
Creating polynomials
If you have an i or a radical, make another one that is the opposite sign
3i → -3i
Once that is done, duplicate existing terms (numbers) until you reach the degree you need
Then multiply out
If you have to multiply things with 3 terms (x + 1 + i)(x + 1 - i) use a 3x3 box
Put terms along the side and top
Multiply into the boxes
Add
Combine like terms
Rational Zeroes Theorem
The rational zeros will be equal to in lowest terms, where p is factors of the constant (last term) and q is factors of the leading coefficient (first number)
List all factors of the last number with a plus and minus sign in front of each on top
List all factors of the first number with a plus and minus sign in front of each on the bottom
Rewrite as numbers and fractions
Descartes’ Rule of Signs
The number of positive zeros is the same as the number of sign changes in the original function, or an even number less
If you get 4, the number is 4, 2, or 0
The number of negative zeros is the same as the number of sign changes in P(-x)
Switch the signs of the odd degree terms
Count sign changes in the original and the -x
Make a table with positive, negative, and complex
Start with the highest number of positive and negative zeros, putting complex next to it if needed to fulfill the number of zeros (equal to highest degree)
2, 2, 0
Then put the lower number of negative zeros in the next row, filling in the difference with complex numbers
2, 0, 2
Put the lower number of positive zeros and the higher number of negative zeros
0, 2, 2
Finally put the lowest number of each and fill in with complex
0, 0, 2
Finding zeros of a function
Check for 1 and -1 first
Add up all the coefficients, if the sum is 0 then 1 is a zero
Add up all coefficients of f(-x), if the sum is 0 then -1 is a zero
Synthetic divide by 1 and/or -1 if they are zeros
Use the calculator to peek at what a zero might be
Synthetic divide (if the remainder is 0 you found one)
After each synthetic division use the quotient for the next division to make it faster
Once you get a quadratic factor the quadratic
If it cannot be factored use the pythagorean theorem to find radicals/imaginary solutions
List solutions in set notation
x = {2, 3, 9} or x ∈ {2, 3, 9}
Write the factored form based on the solutions if necessary
Graphing a polynomial
Leading term test
If the term is positive, the right side goes up
If the term is negative, the right side goes down
If the degree is odd, the function behaves like a line (opposite directions)
If the degree is even, the function behaves like a parabola (same direction)
Write rises or falls
To find the relative maxima/minima, use the calculator (2nd trace)
To find the x-intercepts, find the zeroes using synthetic division (show work)
To find the y-intercept, use the constant (last term) and write f(0) (or whatever letter) as work
Graph by plotting all points (add some if needed) and connect the dots
Zero-multiplicity-cross/touch tables
Factor and find zeros like normal
Put the zeroes in the first column
Determine the multiplicity (how many times each zero appears)
Decide if cross or turning point
Maximum # of turning points = highest degree - 1
Cross if odd multiplicity, tp if even