SCH4U - Unit 2
Energy
Energy - The capacity to do work
Measured in Joules(J), where 1 J = 1 kgxm2/s2
1 kJ = 1000J
Calorie - The energy needed to raise the temperature of 1g of water by 1 K
1000 cal = 1Kcal, or 1 food calorie
Thermal Energy - The energy associated with the random motion of atoms and molecules
Chemical Energy - Energy stored within the bonds of chemical substances
Kinetic Energy - Energy due to motion
EK = mv2/2
Potential Energy - Energy due to position, that gives it the ability to do work
Eg = mgh
First Law of Thermodynamics - The total energy of the universe is constant and can neither be created nor destroyed, only transformed
Internal Energy - The sum of all kinetic and potential energies of all the atoms and molecules in a substance
Et = EK + EP
For instance, an object thrown upwards will slow as it moves upwards, but then speed up as it falls due to gravity, yet always have constant internal energy
Upwards, kinetic energy decreases while potential energy increases
Downwards, kinetic energy increases while potential energy decreases
Work
The change in internal energy is equivalent to the heat transferred and the work done
ΔEt = q + W
If q is positive, heat is absorbed by the system
If q is negative, heat is released by the system
If W is positive, work is done on the system
If W is negative, work is done by the system
Expansion Work - The work done when a system changes size
If work is 0, the internal energy is equal to the heat transferred
W = F(d), or W = -P(ΔV)
q = mCΔt
System - The area being studied
Open System - A system which allows energy and matter to be transferred
Closed System - A system which allows energy to be transferred, but not matter
Isolated System - A system which allows neither energy nor matter to be transferred
Surroundings - Everything outside of a system
Enthalpy
Enthalpy - The value, represented by H, used to quantify the heat flow in or out of a system at a constant pressure
Heat - The transfer of thermal energy
Temperature - The average kinetic energy of the molecules of a substance
Specific Heat - The amount of heat required to raise the temperature of one gram of a substance by one degree Celsius/Kelvin, represented by C
H = Et + PΔV
When no work is done, ΔH = q
ΔH = Hproducts - Hreactants
ΔH - The heat released or absorbed during a reaction at a constant pressure
If ΔH is negative, heat is released
If ΔH is positive, heat is absorbed
Exothermic - A reaction which releases heat into the surroundings
Endothermic - A reaction which absorbs heat from the surroundings
Calculating ΔH:
Calorimetry
Uses a calorimeter, which contains the reaction within water
If heat is absorbed by the water, then the reaction released an equivalent amount of heat
If heat is released by the water, then the reaction absorbed an equivalent amount of heat
Use q=mCΔT to find q, then used ΔH=q/n to find molar enthalpy
Hess’s Law - The energy transferred in a reaction is the same in a multi-step reaction if the reactants and the products are the same
Rearrange given equations so the necessary substances are correctly on the reactant or product side
If a reaction is reversed, the ΔH will become its opposite
Multiply each reaction by coefficients to match the coefficients in the desired equation
Write all of the equations as one large equation with all the reactants on one side, and all of the products on the other
Combine like substances and cancel any product that appears in equal amounts on both sides
Add together all of the ΔH values to find the ΔHrxn
Heats of Formation - The heat change for a substance being formed at a standard state, represented by ΔHfo, that is a measurement of the stability of the substance
The heats of formation of an element is 0
Find the necessary heats of formation in their correct state
Multiply by any coefficients, as necessary, to represent the energy in the reaction
Add together all of the energy of the reactants and products separately
ΔHrxn = ΔHfo(total products) - ΔHfo(total reactants)
Change of Phase
For a substance that remains at the same phase as it changes heat energy, all of the energy causes the molecules to change in temperature, so q=mCΔT can be used to calculate heat energy absorbed or released
When substances change phases, the change in heat is used to break apart or form bonds and altering the shape/potential energy, rather than increase or decrease temperature
Heat of Fusion - The amount of energy required to change 1 gram of pure substance from solid to liquid at its melting point
The energy absorbed or released when a substance changes between a solid and liquid
Qsolid = mHF
Heat of Vaporization - The amount of energy required to convert 1 gram of pure substance from liquid to gas at its boiling point
The energy absorbed or released when a substance changes between a liquid and a gas
Qliquid = mHV
This value is generally lower than the heat of fusion
When going from a solid to a liquid, only some bonds need to be broken, whereas when going from a liquid to a gas, all bonds must be broken
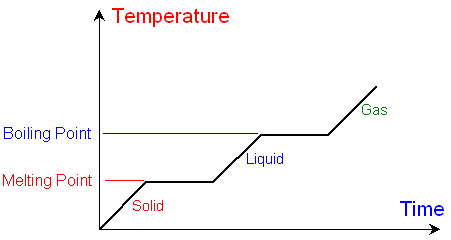
When finding the heat energy of a substance that spans multiple phases, q=mCΔT and the heat of fusion/heat of vaporization must be calculated
Consider that some substances may have different heat capacities at different phases
Once all pertinent q values are solved for, they can be added
Entropy
Second Law of Thermodynamics - The state of entropy of the entire universe will always increase over time, and the entropy can never be negative
All things in the universe tend towards chaos
Entropy - The disorder or randomness of a system, represented by S
The less attraction between molecules, the more disordered it becomes
ΔSuniverse = ΔHsystem/T + ΔSsystem = ΔSsurroundings + ΔSsystem
For example, when a system warms up, it becomes more disordered, and the surroundings become ordered
When something dissolves, the system becomes more disordered
If ΔS is positive, the system becomes disordered
If ΔS is negative, the system becomes ordered
Gibbs Free Energy
Gibbs Free Energy - The amount of energy absorbed or released by the equation which indicates spontaneity
ΔGrxno = ΔHrxno - TΔSrxno
ΔGrxno = ΔGfo(total products) - ΔGfo(reactants)
If ΔG is positive, the reaction is non-spontaneous
Favours reactants
If ΔG is negative, the reaction is spontaneous
Favours products
If ΔG is zero, the reaction is at equilibrium
Products and reactants are equally favoured
ΔH | T | ΔS | ΔG |
(-) | any | (+) | (-) spontaneous |
(+) | any | (-) | (+) non-spontaneous |
(-) | High | (-) | (+) non-spontaneous |
(-) | Low | (-) | (-) spontaneous, enthalpy driven |
(+) | High | (+) | (-) spontaneous, entropy driven |
(+) | Low | (+) | (+) non-spontaneous |
To find the point at which ΔG goes from positive to negative, set ΔG to 0, and isolate for T
T = ΔHrxn/ΔSrxn
When a solid is dissolved in a solvent, although it requires heat to break bonds, it becomes very disordered, and thus makes the overall reaction spontaneous
K Constant and Equilibrium
Equilibrium Constant - The ratio between the concentrations of the products and reactants at equilibrium, represented by K
ΔGrxno = -RT(lnK)
R = 8.314J/K
If K>1, the reaction is spontaneous
If K<1, the reaction is non-spontaneous
ΔGrxn new = ΔGrxno + RT(lnQT)
Use when the reaction does not happen at a standard state
QT represents the reaction quotient
Q = (product of reactants)/(product of products)
Each reactant and product should be raised to its order
If more reactants are added, Q becomes smaller, and the whole reaction will become more spontaneous
Coupled Reactions
When one desired reaction is thermodynamically unfavourable, it can be coupled with a thermodynamically favourable reaction that produces a product that makes the initial reaction more favourable
These reactions share at least one common intermediate
The overall ΔG will be less than zero to make this multi-step reaction product-favoured
Reaction Rates
Factors that cause the reaction rate to increase
An increase in the concentration of reactants
Higher temperatures
Adding catalysts which help the molecules interact/collide
Increasing pressure
Existing in a state with less/weaker intermolecular forces
Rategas > Rateliquid > Ratesolid
Mixing the reactants
Average reaction rate of disappearance for reaction A→B
RateAvg = -Δ[A]/Δt = Δ[B]/Δt
For reaction A→2B
RateAvg = -Δ[A]/Δt = Δ[B]/2Δt
The average rate decreases as the reaction proceeds because there are fewer collisions between the reactant molecules
Instant reaction rate
Solve for using rate laws
Rate = k[reactant]m
k is the rate constant
If k is large, there will be a rapid reaction
If k is small, it will be a small reaction
m is the rate order
If there are multiple reactants, multiply each with their individual order
Rate = k[reactant1]x[reactant2]y…
Orders of Reactions
To determine the order of a reactant:
Find two reactions where the concentration of only one reactant (the one being observed) changes
Find the factor by which the concentration changes
Find the factor by which the initial rate changes
If the factor of concentration is a value other than one, and the factor of the initial rate is one (not changing), that reactant is zero order
e.g., If the reactant doubles, the initial rate does not change
If the factor of concentration and the factor of the initial rate are equal, that reactant is first order
e.g., If the concentration doubles, the initial rate doubles
If the factor of concentration is the square root of the factor of the initial rate, that reactant is second order
e.g. If the concentration doubles, the initial rate quadruples
Repeat for all reactants individually
To determine the order of a reaction:
Add together the orders of each individual reactant
Zero order reaction - Rate = k[A]0
First order reaction - Rate = k[A]1
Second order reaction - Rate = k[A]2
Integrated Rate Laws
When considering time in relation to reaction rates, integrated rate laws must be used
Zero order reaction - [A]t = -kt + [A]i
First order reaction - ln[A]t = -kt + ln[A]i
Second order reaction - 1/[A]t = +kt + 1/[A]i
When graphing concentration as a function of time, the relation of t to [A] can indicate what order the reaction is
Zero order - [A]
First order - ln[A]
Second order - 1/[A]
To find half-life, use the following equations
Zero order - t1/2 = [A]i/2k
First order - t1/2 = 0.693/k
Second order - t1/2 = 1/k[A]i
Collision Theory
As temperature increases, the rate constant k increases because it is temperature dependent
Collision Theory Model - Molecules can only react if they collide in the right orientation with enough energy to cause bond breakage
Activation Energy - The amount of energy required to break bonds, represented by Ea
It is the minimum amount of energy required to start the reactant
As temperature increases, the fraction of molecules that can overcome the activation energy increases
f = e-Ea/RT
An increase in temperature by 10 degrees causes the fraction of colliding molecules doubles, and thus the rate constant doubles
Arrhenius’s Math
k = Ae-Ea/RT
Frequency Factor - The number that represents the likelihood that collisions would occur with the proper orientation for a reaction, represented by A
The greater the frequency factor is, the probability and speed of the reaction will increase
It is temperature dependent
A = (fraction of collisions with proper orientation)(collision frequency)
A changes slightly with temperature
ln(k) = -Ea/RT + ln(A)
To solve for Ea, k must be determined
ln(k) plotted against 1/T should create a straight slope
The slope is -Ea/R, or -Ea/8.314
The y-intercept is A
ln(k2/k1) = Ea/R x (1/T1 - 1/T2)
Uses two different temperatures and rate constants
The rate constant is proportional to the rate
Reaction Mechanisms
Reaction Mechanism - The sequence or steps of smaller reactions that describes the actual process by which reactants become products
Reactions can be made of multiple elementary reactions
One step of a multi-step reaction will always be slower, and thus determine the rate of the overall equation
Observing this rate can determine the overall rate law
Intermediate - A highly reactive and unstable substance produced during a middle step of a chemical reaction
It will be produced and then consumed
They are not in the initial step or final product, and thus, not used in rate laws
Catalyst - A compound that increases the rate of a chemical reaction, but is not consumed
It will exist as both a reactant and a product
They change the mechanism of the reaction and decrease the activation energy
Heterogeneous Catalyst - A catalyst which is not the same state as the reaction materials
Homogenous Catalyst - A catalyst which is the same state as the reaction materials
Enzyme - A biological catalyst
Steady State Approximation - The assumption that the rates of forward and reverse reactions are equal in reactions with a fast first step
Rateforward = Ratereverse
k1[A] = k-1[A]
This value can be substituted in the rate law to determine the slower rate
Rate = (k2k1)[A]/k-1
(k2k1)/k-1 = K
K is the overall rate constant
The overall sum of all elementary reactions, once simplified, should result in the overall balanced reaction, and it must equal the determined rate law
Transition State - The point of a reaction where the activated complex has partially formed product bonds and partially broken reactant bonds, and potential energy is at the highest
The energy difference required to get from the reactants to the activated complex is the activation energy
The greater the activation energy required, the slower the reaction rate becomes
It becomes harder to collide and overcome this energy barrier
RT ln(kcat/kuncat) = Ea uncatalyzed - Ea catalyzed