1.1

Conic section- Shapes that are obtained by taking different plane slices through a double cone

Menaechmus (Greek mathematician) discovered conic sections around 350 BC

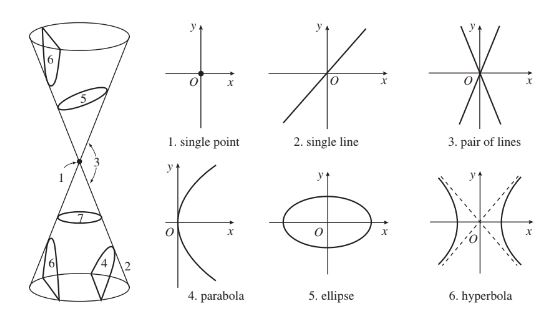
• Slice 7 is considered an ellipse

  • Ellipse- An area where the sum of the distances from 2 fixed points on the plane remain constant

• The ellipse and the hyperbola both have a centre

• Non-degenerate conics- conics that are parabolas, ellipses, or hyperbolas

• Degenerate- A single point, line, and pair of lines

1.1.2 Circles

• Circle- a type of conic, a set of points that lie at a fixed distance (radius), from a fixed point (centre)

• Use the techniques of coordinate geometry to find the equation of a circle with given centre and radius.

• Theorem 1: The equation of a circle with centre (a,b) and radius r is (x-a)^2 + (y-b)^2 = r^2

• Why?

  • This is a variation of the distance formula (d= (x1-x2)^2 + (y1-y2)^2)

Example Problems

Write the equation for the given centre and radius

(a) centre the origin, radius 1

(1)^2 - (x-0)^2 + (y-0)^2

1= x^2 + y^2

x^2 + y^2 -1 = 0

(b) centre (3, 4), radius 3

(3)^2 = (x-3)^2 + (y-4)^2

9= (x-3)(x-3)+ (y-4)(y-4)

9 = x^2 + y^2 -6x -8y + 25

x^2 + y^2 -6x -8y +16=0

Determine the condition on the numbers f, g, and h in the equation x^2 + y^2 + fx + gy + h = 0 for the equation to pass through the origin

Explanation:

• This is the factored/ distributed form of our original equation

• We have to find the state of the equation when a and b equal zero…. (x-0)^2 and (y-0)^2

• We can factor our this form to see the conditions

• This would mean that f,g, and h all must equal 0

(c) Consider the set of points (x,y) that satisfy the equation: x^2 + y^2 -4x +6y +9 = 0

1. Our goal is to complete the square (note that the coefficients on x^2 and y^2 are both 1)

2. Re-write equations containing just the x-terms, and just the y-terms

   x^2 − 4x = (x − 2)^2− 4

   y^2 + 6y = (y + 3)^2 − 9

3. These terms can be substituted into our original equation

   (x-2)^2 -4 + (y+3)^2 -9 +9 = 0

   (x-2)^2 + (y+3)^2 = 4

4. This means that the circle has a radius of 2 and a centre of (2, -3)

Theorem 2: You can complete the square in the equation x^2 + y^2 + fx + gy + h = 0 to put it in the form (x+1/2f)^2 + (y+1/2g)^2 = 1/4 f^2 +1/4g^2 -h

This equation represents a circle with the centre (-1/2f, -1/2g) and a radius sqrt(1/4f^2 + 1/4g^2 -h)

This only occurs when the 1/4f^2 + 1/4g^2 -h is greater than zero, if this is less than zero, we can prove that the figure is not a circle

Why?

The equation is equal to r^2 (radius squared), when any number is squared, it has to equal a positive number. Also, when you go to take the square root of this side of the equation, it is impossible to get a rational answer when square-rooting a negative number.

(d) Determine the centre and radius of the equation

3x^2 + 3y^2 − 12x − 48y = 0.

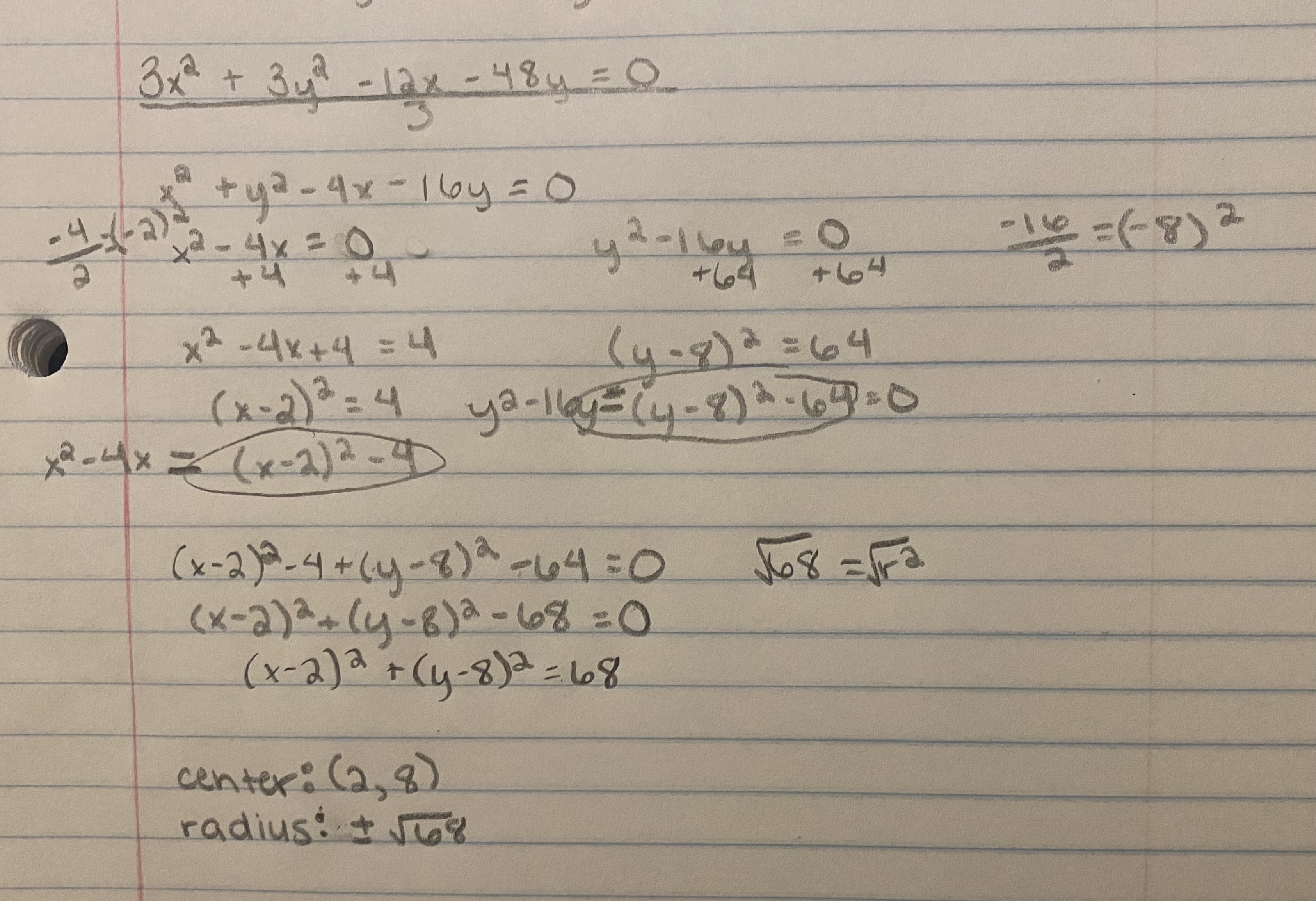
(e) Determine the set of points that satisfies the following equation

x^2 + y^2 − 2x + 4y + 5 = 0;

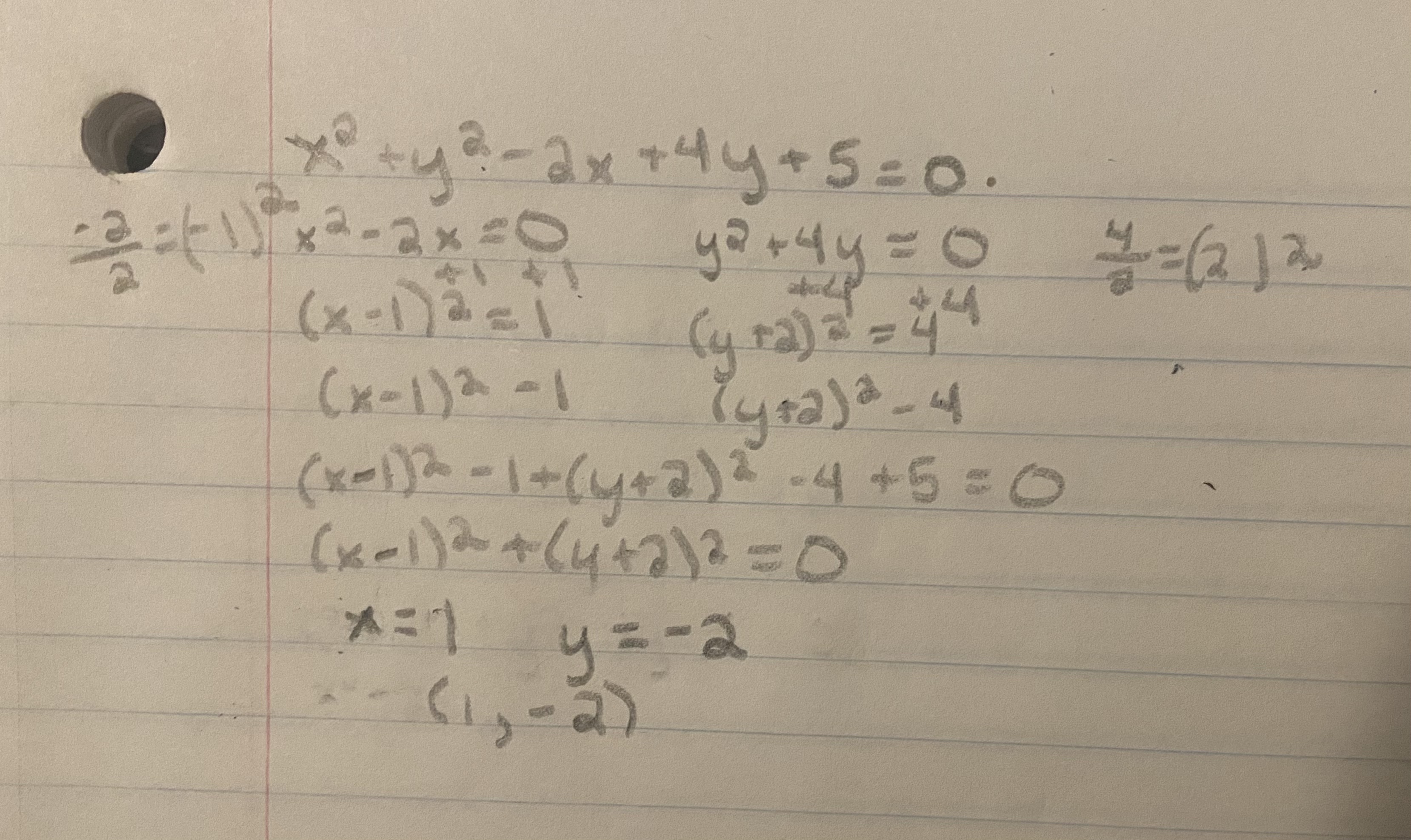
Orthogonal Circles

Two intersecting circles that meet at right angles

Theorem 3: Orthogonality test

Two intersecting circles with equations x^2 + y^2 + f1x + g1 y + h1 = 0 and x^2 + y^2 + f2x + g2 y + h2 = 0, are only orthogonal if f1 f2 + g1g2 = 2(h1 + h2).

Why?

This can be tested with the pythagorem theorem, where P is a point of intersection, and A and B are points inside of each of the circles. This means that

AP^2 + BP^2 = AB^2. Using our previous formulas, we know that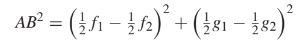

This can be solved to result in the original equation

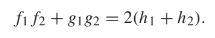
Circles Through Two Points

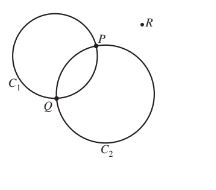
• In this image, the circle intersects at distinct points P and Q

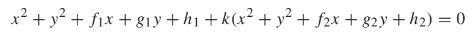
This equation represents a circle when k does not equal -1, and this means that P and Q will satisfy the equation

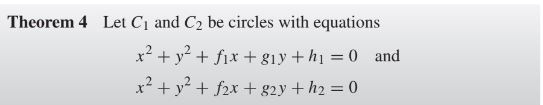
Explanation:

These circles have distinct points of intersection, and the line containing these points can be expressed using the second equation, only when k=-1. When k is any other number, this is the equation of one of the circles

1.1.3 Focus-Directrix Definition of the Non-Degenerate Conics

• The three non-degenerate conics are the parabola, ellipse, and hyperbola

  • The distance of a set of points from a fixed point (focus) follow a constant multiple (eccentricity)

  • This distance is also followed from a line (directrix)

• Eccentricity- It is an ellipse if e (eccentricity) is between 0 and 1, a parabola of e equals 1, and a hyperbola is e is greater than 1

Parabola (e=1)

• The set of points (P) whose distance from a fixed point (F) is equal to their distance from a fixed line (D)

• Standard form:

  • The focus must lie on the x-axis, and have coordinates (a,0) and a must be greater than 0

  • The directrix must be x=-a

• y^2=4ax

  • This equation is used to show that each real number corresponds with one number on the parabola

• The focus and directrix can be described by

  x = at^2, y = 2at (t ∈ R).

• The x-axis is the axis of the parabola in standard form because the parabola is symmetric in respect to this line.

• The origin is the vertex of the parabola, and it has no centre

Ellipse

• e is greater than or equal to zero, but less than one

• A set of points whose distance from a certain point is e times their distance from a fixed line

• Standard form:

  • The focus (point) must lie on the x-axis, and have coordinates (ae, 0), with a being greater than 0

  • The directrix must follow the equation x=a/e

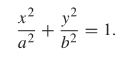
• This equation continues to grow, however, as the figure is symmetrical.

• There is a second focus (-ae, 0) and a second directrix (-a/e)

• The ellipse intersects the axes at the points (±a, 0) and (0, ±b).

  • Major axis- the segment joining the points (±a, 0)

  • Minor axis- the segment joining the points (0, ±b)

    • The minor axis will always be shorter than the major axis because a is greater than b

• Parametric equations:

  x = a cost, y = b sin t (t ∈ (−π, π]).

Hyperbola

• e is greater than 1

• Standard form:

  • The focus (point) must lie on the x-axis, and have coordinates (ae, 0), with a being greater than 0

  • The directrix must follow the equation x=a/e

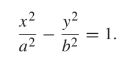
When: b^2 = a^2 (e^2 − 1), a > 0, e > 1.

• Foci (±ae, 0) and Directrices x = ±a/e

• Parametric equations: x = a sec t, y = b tan t (t ∈ (−π/2, π/2) ∪ (π/2, 3π/2)).

• Asymptotes- the lines of the parabola that the branches grow closer to. They are notated as y = ±(b/a)x

Rectangular Hyperbola

• e= sqrt (2)

• This means that e^2=2 and a=b

• The asymptotes have the equation y = ±x, so they are at right angles

  • A hyperbola whose asymptotes are at right angles is called a rectangular hyperbola

• You can use the asymptotes as new x and y axes, and the equation can then be written as xy = c^2

  • The origin will always be at the center in this form

Parametric equations: x = ct, y = c/t where t = 0.

Polar Equation of a Conic

• You can describe the equation of a non-degenerate conic in terms of polar coordinates

  • Polar coordinates: r and θ

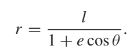
This formula comes from the equation OP = e · PM where the distance from the origin to a point is equal to the eccentricity multiplied by the distance between that same point and the directrix.

1.1.4 Focal Distance Properties

Theorem 5: The sum of the two focal distances from a point always equal double the major axis.

Why?

The distance from a point to either foci is equal to the eccentricity times the distance from said point to the directrix. This distance is equal to the distance from the second foci to to second directrix (d’ and f’). When adding these two distances, they will always equal 2a (double the major axis)

Theorem 6: Differences of Focal Distances of Hyperbola

• If a point (P) is closer to F, then PF’ - PF = 2a

• If P is closer to F’ then PF’ - PF = -2a

• |PF − PF| is constant for every point on the parabola

1.1.5 Dandelin Spheres

A slant plane (pi) that cuts one portion of a right, circular cone is an ellipse

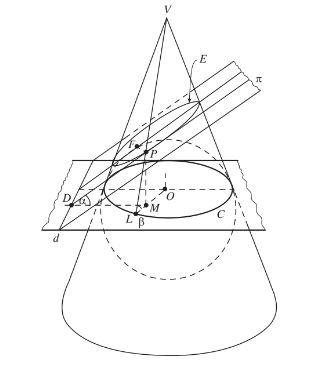
1.2 Properties of Conics

1.2.1 Tangents

Goals: Find the slope of the line that is tangent to the curve at the parameter, so that you can determine the equation of the tangent

Theorem 1: The slope of a tangent to a curve is y’(t)/ x’(t)

Theorem 2: Equations of tangents in standard form

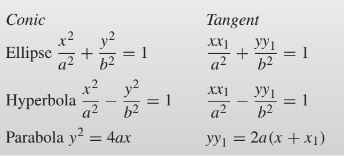
Polar of (a,b) with respect to the unit circle

• If (a,b) is some point on a tangent, then it can be determined that ax1 + by1 = 1 because of the equation xx1 + yy1 = 1. This equation can be re-written with points x2 and y2, which deduces the fact that points

  ( x1, y1) and (x2, y2) are on the same line, and this line is called the polar of (a,b) with respect to the unit circle

Theorem 3: When a point (a,b) lies outside of the circle, and the tangents from point (a,b) touch the circle at P1 and P2, then the equation of the line is ax + by = 1

• Normal of a curve- the line through a point that is perpindicular to the tangent of a curve at said point

  • To find the equation of a normal of the curve, you find its slope and the coordinates of the point on the parabola where they intersect

1.2.2 Reflections

Reflection law- The angle that incoming light makes with the tangent to a surface is the same as the angle that the reflected light makes with the tangent.

• Applies to all mirrors, whether plane or curved

• Mirrors are often designed to have a conic curve

Reflection property of the Ellipse - light which comes from one focus of an elliptical mirror is reflected at the ellipse to pass through the second focus.

Reflection property of the hyperbola- light coming from one focus of a hyperbolic mirror is reflected at the hyperbola and makes the light appear to have come from the other focus (Internal Reflection property). Light going towards one focus is reflected towards the other focus (External Reflection Property)

Reflection Property of the Parabola- incoming light parallel to the axis is reflected at the parabola to pass through the focus. Light coming from the focus of a parabola is reflected to give a beam of light parallel to the axis of the parabola

1.2.3

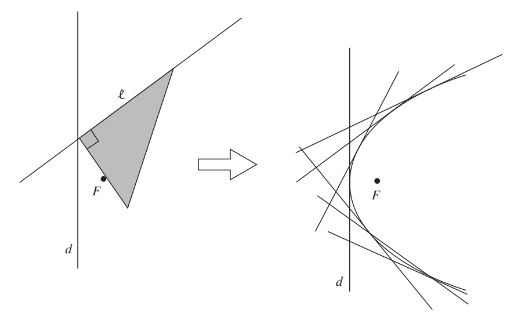
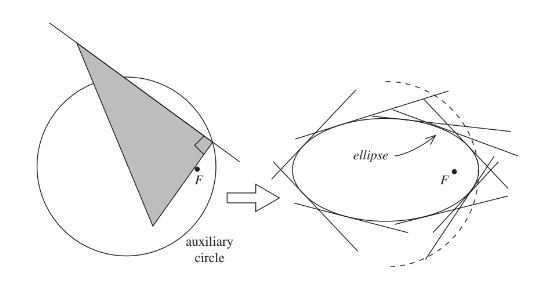
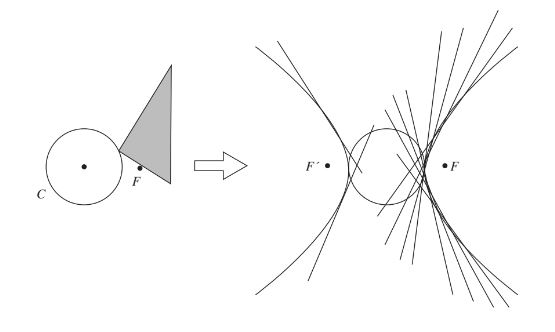
• Non-degenerate conics are the envelopes of a family of lines that are tangent to the conics

  • The conic being constructed is the curve in the plane that has each of the lines in the family as a tangent

• Auxiliary circle- A circle whose diameter is its major axis

  • The tangent to a parabola at its vertex is the auxiliary circle of the parabola

  Theorem 4: A perpindicular from a focus of a non-degenerate conic to a tangent meets the tangent on the auxiliary circle of the conic

  • When given a parabola and its axis, this theorem is used to identify the focus

Envelope Drawings

Parabola:

Ellipse:

Hyperbola:

1.3 Recognizing Conics

Standard form of conics- the centre is at the origin, and the axes are parallel to the x and y axis

• Equations of all non-degenerate conics follow this equation in standard form:

  • Ax^2 + Bxy + Cy^2 + Fx + Gy + H = 0,

• Any non-degenerate conic can be determined from a conic in standard form using a rotation (x, y) → (x cos θ − y sin θ, x sin θ + y cos θ) followed by a translation (x,y) → (x-a, y-b)

• Both tranformations are linear, so the equation of the conic at each stage is just a second degree of the original equation

Matrices

Matrix form of the equation: x^T Ax + J^T x + H = 0.

• Look back at the old equation: Ax^2 + Bxy + Cy^2 + Fx + Gy + H = 0

  • The values from this form are used to plug into the matrix form

  • 

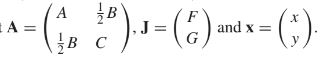
Theorem 2: A 2x2 matrix P represents a rotation of R^2 when P is orthogonal and the det of P = 1

Classify a conic (E) with the equation Ax^2 + Bxy + Cy^2 + Fx + Gy + H = 0

1. Write the equation in matrix form (x^T Ax + J^T x + H = 0)

2. Determine the orthogonal matrix P, with a determinant of 1 that diagonalizes A

3. Make the change of coordinate system x=Px’. This changes the equation to λ1x’^2 + λ2 y’^2 + f x’ + gy’ + h = 0

   1. λ1 and λ2 are the eigenvalues of A

4. Complete the square to rewrite the equation of E into (x’’, y’’) as the equation of a conic in standard form

5. Use the equation x’ = P^Tx to determine the centre and axes of E in the terms of the original coordinate system.

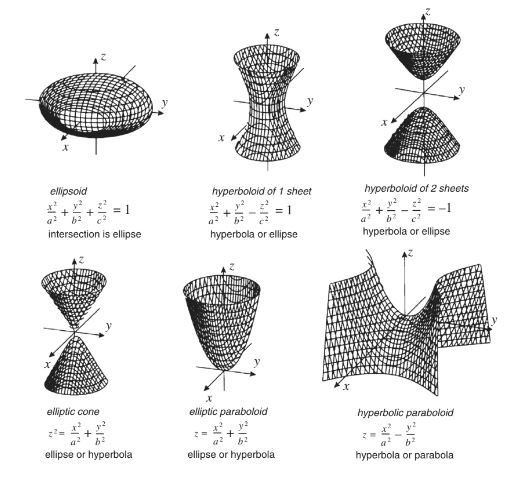
1.4 Quadric Surfaces

• Quadric surfaces- (quadrics) surfaces in R^3 that are the natural analogues of the conics.

  • Ax^2 + By^2 + Cz^2 + Fxy + Gyz + Hxz + Jx + Ky + Lz + M = 0

• Degenerate quadrics- Empty set, single point, single line, single plane, pair of planes, and a cylinder

  • Cylinder- any surface that consists of an ellipse, parabola, or hyperbola in some plane

1.4.2

• Use the orthogonal diagonalization of 3x3 matrices to classify non-degenerate quadrics, similarly to how 2x2 matrices were used to classify conics

Idetifying matrices: In the equation Ax^2 + By^2 + Cz^2 + Fxy + Gyz + Hxz + Jx + Ky + Lz + M = 0,

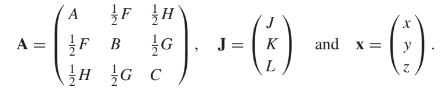
If a 3x3 matrix (P) represents a rotation of R^3 about the origin when P is orthogonal and det P = 1

Classify quadric E with the equation Ax^2 + By^2 + Cz^2 + Fxy + Gyz + Hxz + Jx + Ky + Lz + M = 0,

1. Write the equation in matrix form (x^T Ax + J^T x + M = 0)

2. Determine the orthogonal matrix P, with a determinant of 1 that diagonalizes A

3. Make the change of coordinate system x=Px’. This changes the equation to λ1x’^2 + λ2 y’^2 + λ3 z’^2 + jx’ + ky’ + lz” +m = 0

   1. λ1, λ2, and λ3 are the eigenvalues of A

4. Complete the square to rewrite the equation of E into (x’’, y’’, z’’) as the equation of a quadric in standard form

5. Use the equation x’ = P^Tx to determine the centre and axes of E in the terms of the original coordinate system.

1.4.3 Rulings of Quadric Surfaces

Ruled Surface in R^3- a surface that can be made up from a family of straight lines

Hyperboloid of One Sheet

• x^2 + y^2 - z^2 = 1

• The surface meets each horizontal plane in a circle whose centre lies on the z-axis

• The surface meets each plane containing the z-axis in a rectangular hyperbola

• Family of Generators- (generating lines) straight lines that construct the hyperboloid

• Ruled surface- surface created by the generating lines

  • There is a second family of lines that are also generators of said surface, these lines are rotated around the z-axis

  • The lines that share a family never meet, but the lines of opposite families will always meet

Theorem 2: A hyperboloid of one sheet contains two families of generating lines, The members of each family are disjoint, and each member of either family intersects each member of the other, with exactly one exception

Hyperbolic Paraboloid

• Theorem 2 is also valid for this figure