The Valuation Principle
Cost Benefit Analysis
• Most business decisions involve the evaluation of the benefits generated compared the costs incurred creating the benefits.
• If the benefits exceed the costs value is created.
• Example: You have an opportunity buy two tickets to this year’s Super Bowl on February 11th in Las Vegas, NV. They are located in section 242, Row 11 in Allegiant Stadium.
• If they cost you $1000 per ticket, would buy them?
Value Creation – Could We create value
• You need to know costs and benefits.
• These values represent “prices” as measured in cash today.
• You can create value if you can buy at a lower price and sell at a higher price.
• Supply and Demand will set this price.
Competitive Market Prices
• What do you think the price of these tickets will be in a competitive market?
• What factors will impact this price?
• Does it matter whether or not you want to go to the Super Bowl?
The Valuation Principle
• Competitive Markets
– Markets where goods can be bought and sold at the same price.
• The Valuation Principle
– Values of assets to individuals and firms are determined by their competitive market prices.
– The benefits and costs must be evaluated using those market prices.
– When the value of the benefits exceeds the value of the costs the decision increases the value of the firm.
Applying the Valuation Principle
• If all decisions involved costs and benefits occurring at the same time and resulting from competitive market prices establishing the value created would be simple.
• Most financial decisions involve costs and benefits occurring at different points in time.
• Typically upfront costs create future benefits.
• We must develop a method to account for these timing differences.
• Not all decisions have market prices available (corporate projects).
Introduction to the Timeline
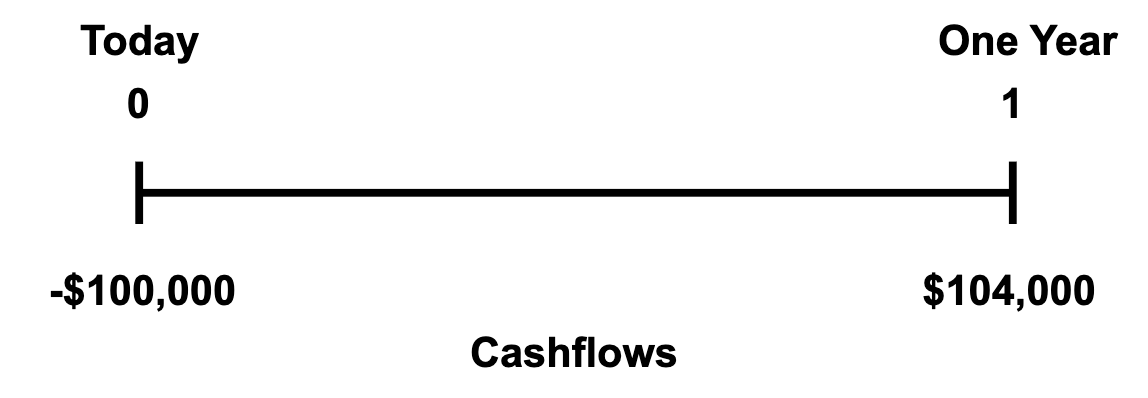
Assume a firm can invest $100,000 in a project today and generate $104,000 in one year
• Is $4,000 the correct measure of value created?
• What if the firm could earn 6% investing in Government Bonds?
• The measure of value created needs to take this alternative investment opportunity into account.
Interest Rates as Prices

• The interest rate earned on the Government Bond is the “price” in the market for money in one year.
• The benefits of buying the Government Bond ($6,000) exceed the benefits of the Investment ($4,000) so you should reject the project.
• We can use the 6% interest rate to establish the market values to compare the cash flows over time.
Time Value of Money
• The difference in value between money today and money in the
future represents the Time Value of Money.

• In this case $1.00 today is equivalent to $1.06 in one year.
• Therefore (1+interest rate) or (1.06) is the interest rate factor.
Time Value of Money
We can use the interest rate factor to establish equivalent value
over time using the Time Value of Money
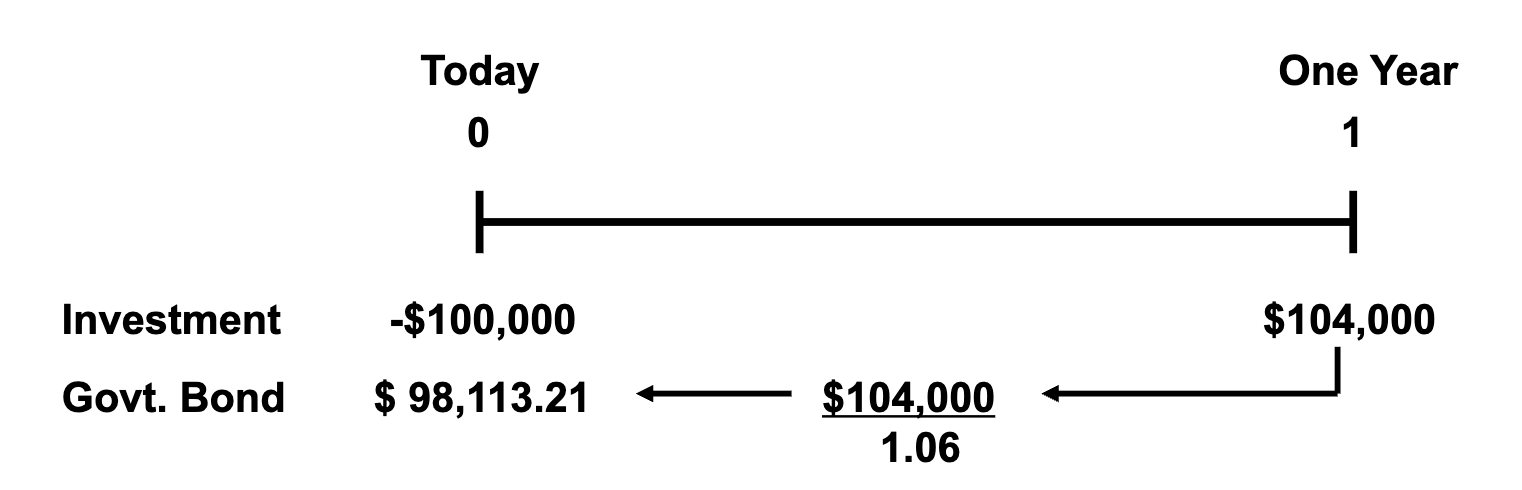
• To compare values over time the interest rate factor adjusts for the “price” of money.
• You should reject this investment because the benefits are less than the costs when compared using market prices.
• The value today of a future cash flow is called the “Present Value.”
Net Present Value
• Since costs and benefits must be compared at the same point in time the practice in finance is to convert all cash flows to Present Values to measure the value created.
• Net Present Value (NPV)
– The difference between the present value of a projects benefits and the present value of it’s costs.
• NPV = PV of Benefits - PV of Costs
Net Present Value
Revisiting our earlier investment opportunity we can see the benefit of calculating NPV

• You should reject this investment because the NPV is negative.
• Value is destroyed by making this investment. The firm would be better off buying a Government Bond
Net Present Value
If the investment could be made for $97,000 using NPV demonstrates that the investment adds value

• You should accept this investment because the NPV is positive.
• Value is created by making this investment. The firm is better off taking the investment than buying a Government Bond.
Net Present Value
The NPV Rule
- “When making an alternative investment decision, select the
alternative with the highest NPV. Choosing this alternative is
equivalent to receiving its NPV in cash today.”
• As long as the interest rate represents the fair market “price” for
money we should use the NPV rule to maximize NPV regardless
of our preference for receipt of cash.
• We can borrow or lend to shift the cashflows to match our
preferences.
The Law of One Price
• Definition - In frictionless markets perfect substitutes must have identical prices.
• Conditions for arbitrage exist when the cumulative net cash flows from combining security positions is never negative and positive in at least one instance.
Arbitrage and Short Selling
• In a short sale an investor sells an security he does not own.
• In practice, this is accomplished by borrowing a security from another investor and selling it to someone else thereby creating a “short” position.
• Some time in the future the investor must return the security they borrowed. This is called “covering” the short position.
• If short positions are can be easily created investors can potentially profit by selling things they believe are overvalued.
Arbitrage Example

The resulting arbitrage profits would be sought out by investors increasing the demand for the $1,000 investment.
This increase in demand would raise the price until the available profits were eliminated
The Law of One Price and NPV
• We will implement the Law of One Price as we explore the pricing of
securities.
• Positive NPV investment opportunities are difficult to find because of
the pressure that competitive markets place on the values of
projects.
